“數(shù)形結(jié)合”讓問題解決靈動起來

鄭英姿

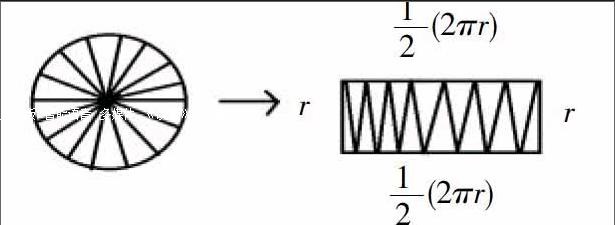
摘要：數(shù)形結(jié)合是一種可以解決數(shù)學問題的有效辦法。小學生通過初步感受數(shù)形結(jié)合思想，有助于他們豐富和加深對數(shù)學知識的理解，也有助于改善學生的思維方式。特別是面對抽象的數(shù)學問題，數(shù)形結(jié)合能化抽象為具體，有效地輔助學生思考。

關(guān)鍵詞：數(shù)學思想；數(shù)形結(jié)合；問題解決

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2017）03-0088

在教學實踐過程中，越來越多的教師發(fā)現(xiàn)學生在解決數(shù)學問題時，難以表示問題之間的聯(lián)系。數(shù)形結(jié)合思想就是將直觀的幾何圖形與抽象復雜的數(shù)量關(guān)系相結(jié)合來分析。在解題的過程中可以根據(jù)題目的具體條件，將數(shù)量關(guān)系轉(zhuǎn)化成圖形問題，并把圖形問題轉(zhuǎn)化成解決問題的方法，從而起到簡化解題思路和優(yōu)化解題途徑的目的。在課堂教學中，引入數(shù)形結(jié)合還可以激發(fā)學生的學習興趣，突出“以學為中心”的教學理念。

一、“問題解決”教學中數(shù)形結(jié)合思想的應用

1. “以形助數(shù)”，啟迪數(shù)學思維

“以形助數(shù)”是指在我們數(shù)學學習過程中，經(jīng)常會有抽象的數(shù)學概念和復雜的數(shù)量關(guān)系，而我們往往可以借助圖形使之形象化、直觀化。把抽象的數(shù)學語言轉(zhuǎn)化為直觀的圖形，便于我們對其進行分析和理解。

例如：筆者在人教版三年級下冊《連乘問題》的教學中，為幫助解決“一箱礦泉水有12瓶，每瓶2元，買4箱一共多少錢？”的數(shù)學問題，分析數(shù)量關(guān)系，專門設(shè)計一個畫圖的活動，請學生獨立思考，把思考的方法用畫圖的方式記錄下來，并根據(jù)圖寫出解決問題的算式。畫圖如下：

活動后每個學生很清晰地根據(jù)自己的圖形將題目中的三個數(shù)學信息建立起數(shù)量關(guān)系，并對它們之間的關(guān)系進行分析。在此活動中，學生的學習參與度很高，激發(fā)學生的學習興趣，并讓枯燥乏味的數(shù)學課堂一下子靈動起來。其次，利用圖形可以幫助學生理清復雜的數(shù)量關(guān)系，幫助學生建立數(shù)感。

2. “以數(shù)解形”，發(fā)展空間觀念

以數(shù)解形就是借助于數(shù)的精確性和嚴密性來闡明形的某些屬性。有些圖形中蘊含著比較多的關(guān)系，學生必須分析圖形和數(shù)字之間的特定聯(lián)系才能正確的解決問題。例如：人教版六年級上冊中有關(guān)圓的知識中，有這樣一道練習題：“已知圓的半徑求長方形周長”如下圖：

初看圖形，但大多數(shù)學生不能馬上得出答案，此時，必須要通過切割、重組等操作過程，將復雜的圖形通過代數(shù)方法來計算出長方形周長。已知圓形的半徑是2厘米，通過觀察，發(fā)現(xiàn)長方形的兩邊長就是圓形的周長，長方形的寬就是圓形的半徑，學生通過長方形周長公式就能算出周長。雖然是計算圖形周長問題通過這樣一道數(shù)形結(jié)合的題目練習培養(yǎng)學生圖形分析的能力，從而提高學生的學習效率。

3. “數(shù)形結(jié)合”，明朗數(shù)學問題

分數(shù)應用題是小學應用題教學的重點和難點，由于抽象程度比較高，學生難以理解和掌握，要較好地解決這個問題，就必須運用數(shù)形結(jié)合的思想。

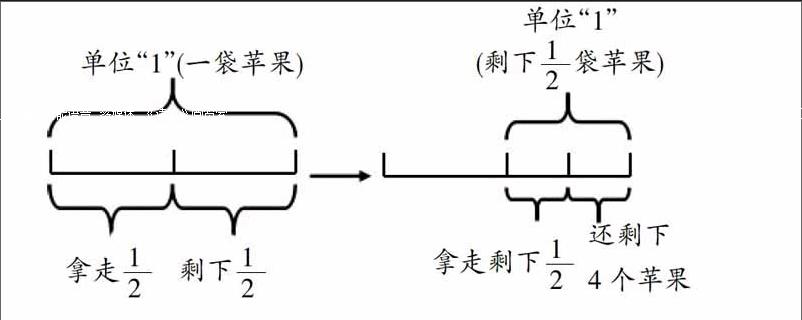
例如：一袋蘋果，第一次拿走整袋蘋果的，第二次又拿走剩下的，最后籃子里還有4個蘋果。你知道原來這個籃子里有幾個蘋果嗎？這道題的難點在于單位“l(fā)”的變化，第一次是把“整袋蘋果”看作單位“1”的量，第二次把“剩下的蘋果”看作單位“1”的量，因此學生在解答時往往會感到困難。只要運用數(shù)形結(jié)合的思想幫助弄清題意，這道題就簡便多了。畫線段圖如下：

從上述線段圖中，可以很清楚地看出，拿走剩下的，還有4個蘋果，那么第一次拿走后“剩下的蘋果”的數(shù)量應該是4個的2倍，即8個。所以，整袋蘋果的數(shù)量就是8個的2倍，即16個，列式為4×2×2=16（個）。如此抽象的思維有了“形”這個橋梁作為依托，思考起來既省時又省力。

二、培養(yǎng)學生數(shù)形結(jié)合思想的策略

1. 分析教材，挖掘知識點背后的數(shù)形結(jié)合意圖

教材分析是教師工作的重要內(nèi)容，教師對教材的分析狀況直接影響著其課程的設(shè)計、組織與實施，從而間接影響著教學質(zhì)量的好壞。數(shù)形結(jié)合是數(shù)學思想很重要的部分，隱藏于數(shù)學知識的背后，需要教師用發(fā)現(xiàn)的眼光去尋找。數(shù)形結(jié)合除了是一種思想的體現(xiàn)，還是解決數(shù)學問題的策略，幫助學分析復雜的數(shù)量關(guān)系，將復雜的數(shù)學問題簡單化。

2. 走進課堂，感受數(shù)形結(jié)合思想

數(shù)形結(jié)合使數(shù)與形之間巧妙的互換，使看上去比較難的問題簡單化、明朗化。因此，在數(shù)學教學中，教師要有意識地利用數(shù)形之間的關(guān)系，幫助學生逐步樹立起數(shù)形相結(jié)合的思想方法，培養(yǎng)主動運用數(shù)形結(jié)合的方法去解題的意識，長期的鍛煉可以使學生將數(shù)形結(jié)合思想內(nèi)化為自己的認知結(jié)構(gòu)中，成為運用自如的思想觀念和思維工具，從而提高學生的數(shù)學修養(yǎng)與解題能力。

3. 練習實踐，體驗數(shù)形結(jié)合的妙用

著名數(shù)學家笛卡爾曾說過：“沒有任何東西比集合圖形更容易人腦里了”。課堂教學的調(diào)查發(fā)現(xiàn)，利用數(shù)形結(jié)合的方法解題，有極其明顯的優(yōu)勢，能夠把抽象的思維表達直觀形象化。因此，在平時的練習中，引導學生利用數(shù)形結(jié)合的方法幫助解決復雜的數(shù)學問題，從而讓學生在解題過程中體驗數(shù)形結(jié)合的妙處，提高學好學習的自信心。

華羅庚先生說過：數(shù)缺形時少直觀，形少數(shù)時難入微，數(shù)形結(jié)合百般好，隔裂分家萬事休。的確，數(shù)形結(jié)合的思想滲透在數(shù)學教學的每一個領(lǐng)域，教師只有在平時的教學中扎扎實實地落實“數(shù)形結(jié)合”的思想，學生才能真正做到見數(shù)思形、見形想數(shù)、以形助數(shù)、以數(shù)輔形，使學生逐步形成數(shù)形結(jié)合思想，并使之成為學習數(shù)學、解決數(shù)學問題的工具，這是數(shù)學教學著力追求的目標。

（作者單位：浙江省溫州市經(jīng)濟開發(fā)區(qū)沙城第三小學 325000）