如何提高高三立體幾何復習課的有效性
【摘 要】高中學習階段作為學生生涯中的第一個轉折點,高考成績直接決定著學生的未來發展。高中數學作為高中教育的重要組成部分,對學生的高考成績影響非常大。對于高中數學來說,幾何知識作為高中數學的難點,特別立體幾何知識,對很多學生來說都是“噩夢”。基于此,筆者重點從而高三立體幾何知識復習作為出發點,探究如何提高高三立體幾何復習的有效性。
【關鍵詞】高中教學;幾何復習課;有效性;高考
引言
總所周知,在高中教學中,高一、高二主要是知識教學,高三主要是知識復習,也是學生面臨高考的沖刺階段,“高考沖刺一百天”是學生高中的最后沖刺階段,因此加強學生復習對學生高考有著重要影響。高中數學作為高中教育的重點與難點,很多學生對高中數學都望而遠之,特別是立體幾何知識,對學生的思維能力與邏輯能力要求非常高。
一、加強立體結合知識的導入環節,采用知識交流的復習形式
由于高三學生的知識基礎已經定型,在復習過程中,由于很多學生對立體幾何知識了解不夠充分,或者運用能力相對較差, 這時就需要教師進行知識導入,先讓學生對知識有一個初步認識或回憶,保障復習內容的階梯型原則。在復習中,無論是知識教學還是數學題教學,都需要引入一些基礎知識,讓學生能夠有一個提前準備或復習,避免學生思維松懈或一直處于緊繃狀態。通過開展階梯型知識層次,這樣才能夠逐漸構建學生的思維結構。例如在“直線、平面平行的判定”中,在正式復習之前,教師需要落實學習過程與學習方法為主,避免以單純的知識講解。通過一系列提問引導學生思維:“觀察教室里黑板面與天花板面所在的平面的交線與教室地面有何關系?”為了能夠培養學生的思維意識,教師可以先讓學生觀察周邊的事物,讓學生養成觀察周邊生活的習慣,從而加強立體幾何知識與現實生活中的聯系。之后再次引導:“為什么平行?怎樣去判斷平面外一條直線與這個平面平行?”通過證明平面外線與這個平面沒有公共點,也即證明這條直線與這個平面內的任何一條直線無交點。通過證明一條直線與無上條在同一個平面內存在的不同位置關系的直線都無公共點,這種情況幾乎是不可能實現的,這時提問學生,如何將“無限”轉變成“有限”。從而得出結論,結論一:“若平面外的一條直線與平面內的一條直線異面,線面是否平行?”;結論二:“若平面外的一條直線與平面內的一條直線平行,線面是否平行?”。之后教師在通過列舉反例:“假設不平行,那么直線與平面必相交,這時直線與平面必有一個交點。現在請同學們判斷一下這個交點與平面內的這條直線有什么位置關系?”通過師生相互提問,相互討論,從而充分展示了問題解決中的“無限”化“有限”的思維軌跡,文中采用的“異面直線的判定”,體現了未知轉化為已知的思維模式。通過整個教學過程展現了一個新定力的形成,從而培養學生的邏輯思維能力,讓學生能夠進一步加深“直線與平面”相關知識的理解深度,最終實現定理條件與結論的復習,在通過采用實際體系引入知識內容,從而提高立體幾何知識教學的有效性。
二、通過試驗,充分分析知識定理
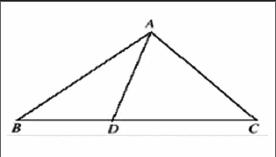
在復習過程中,由于立體幾何知識相對比較從抽象,也就是學生很難用想象理解其中的內涵,為了保障立體幾何知識教學的有效性,教師可以充分發揮學生的主觀性,讓學生自主動手來探究知識,也就是通過的數學試驗,幫助學生解題問題,讓立體幾何通過現實的表現形式呈現出來。教學中,教師可以讓學生準備一個三角形紙片,之后做出實驗內容(如圖),其主要表現在:
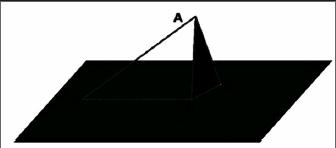
通過△ABC的定點A進行紙片翻折,從而得到折痕AD,之后將折后的紙片豎方在桌面上。之后讓學生分析:第一,折痕AD是否與桌面垂直;第二,如何翻折才能夠讓折痕AD與桌面所在的平面垂直?
通過設置一系列的問題,從而引導學生直觀感受判斷線面垂直的條件,并提問:“折痕AD與桌面一定垂直嗎”“如何翻折才能使折痕與桌面垂直?為什么折痕與桌面是垂直的?”“如果一條直線與平面內的一條直線垂直,能判斷此直線和平面垂直嗎?”“條件中的兩條直線必須相交嗎?(讓學生借助模型推理)”
雖然這些問題對于學習成績較好的學生來說不是問題,但對于大部分學生都比較困難,因此通過學生在操作試驗過程中,能夠借助模型來分析線面垂直的條件,并且能夠在此基礎上再通過幾何繪畫讓學生在紙上畫出相應的條件,或者教師通過動畫展示的形式,加強學生的3D思維,引導學生歸納直線與平面垂直的判定定理,加深學生對判定定理中兩個關鍵條件的認知,即“雙垂直”和“相交”,如圖。
雖然在立體幾何復習過程中,采用該方法比較繁瑣,但很多學生之所以學不好立體幾何知識的根本原因就是學生邏輯性不強,二維圖與三維圖之間會存在一定的視覺差異,如果學生不能充分想象,通過主觀思維構造3D圖形,那么很難提高學生的立體幾何能力,自然也就無法提高自身數學成績。因此,對于立體幾何知識來說,是將多個平面幾何知識進行整合,之后讓學生了解到其中的定理,也就是基礎知識,再加上學生的幾何圖形思維能力,即可解決絕大部分的幾何習題,從而加強學生立體幾何能力。者認為,數學復習需要追求“精”、“準”,而不是一味的追求效率。
三、結束語
高中教育對學生的未來發展有著直接影響,高中數學作為高中教育的重點與難點,必須要做好精準的復習,充分發揮復習課堂的積極作用,保障復習一節課,學生能夠更好的掌握復習知識,不能僅僅針對好學生而復習,必須要保障復習的全面性,也就是所有學生都要照顧到,從而推動全面學生發展。
作者簡介:丁志堅(1963-),男,貴州省貴定縣人,民 族:漢 職稱:中級教師,學歷:本科。研究方向:高中數學教育。
參考文獻:
[1]王春鳳.提高高三數學復習課教學質量的幾點嘗試[J].才智,2016,11:97-98.

