優(yōu)化提問藝術(shù)，建構(gòu)集約型數(shù)學(xué)課堂

曾玉山

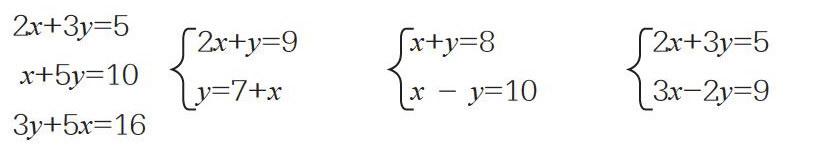
【摘要】構(gòu)建“集約型”課堂離不開課堂的有效提問，如果老師懂得提問的藝術(shù)，在課堂上進(jìn)行有效提問，必將提升課堂效率。筆者作為一名數(shù)學(xué)老師，根據(jù)自身的教學(xué)經(jīng)驗(yàn)認(rèn)為最有效的提問是有指向的提問，要實(shí)現(xiàn)老師與學(xué)生、學(xué)生與學(xué)生之間的多維互動。另外，老師在設(shè)計(jì)問題時(shí)還應(yīng)該注意問題之間的內(nèi)在邏輯，問題之間要有邏輯上的聯(lián)系，最后老師需要根據(jù)學(xué)生的反應(yīng)進(jìn)行適時(shí)追問，完善學(xué)生對知識的認(rèn)識。

【關(guān)鍵詞】初中數(shù)學(xué)；提問藝術(shù)；集約型課堂

在這個(gè)競爭激烈的社會，應(yīng)注重提升課堂效率和教學(xué)質(zhì)量。如何利用有效的課堂時(shí)間提升學(xué)生的學(xué)習(xí)效率值得每一位老師深思。而在這種形勢下，越來越多的數(shù)學(xué)老師已經(jīng)體會到了構(gòu)建集約型課堂的重要性，這種課堂下，老師更加應(yīng)該注重提問的藝術(shù)，老師提出的問題應(yīng)該有所指向以促進(jìn)多維互動，并且應(yīng)該注重問題之間的邏輯關(guān)系，懂得前后呼應(yīng)，而且要在適當(dāng)?shù)臅r(shí)間、適當(dāng)?shù)奈恢脤W(xué)生進(jìn)行追問，完善學(xué)生的結(jié)構(gòu)體系。

一、有所指向，多維互動

提問要講究藝術(shù)，老師在設(shè)置問題時(shí)要考慮到不同層次的學(xué)生，切不可將問題設(shè)置得太難，這樣幾乎只有學(xué)習(xí)好的幾名學(xué)生回答出來，也不可將問題設(shè)置得太簡單，這樣不能夠促進(jìn)學(xué)生思考。老師應(yīng)該根據(jù)班上學(xué)生的學(xué)習(xí)情況有指向地對學(xué)生進(jìn)行提問，既能照顧到不同層次的學(xué)生，還可以促進(jìn)學(xué)生思考，這樣才能實(shí)現(xiàn)老師與學(xué)生、學(xué)生與學(xué)生之間的多維互動，提升課堂效率。

例如，我在為學(xué)生們講解二元一次方程和二元一次方程組的相同點(diǎn)及區(qū)別時(shí)，先為學(xué)生們舉了幾個(gè)例子，從這幾個(gè)例子中學(xué)生們可以觀察出二元一次方程與二元一次方程組的相同點(diǎn)與區(qū)別。我先讓學(xué)生觀察了下面幾個(gè)例子：

我事先已經(jīng)告訴學(xué)生們前面三個(gè)是二元一次方程，而后面的是二元一次方程組，我先讓那些學(xué)習(xí)不是特別好的學(xué)生回答，第一位學(xué)生回答道：“兩者的相同點(diǎn)是他們都有兩個(gè)未知數(shù)，區(qū)別是二元一次方程只有一個(gè)方程，而二元一次方程組則是由兩個(gè)二元一次方程組成的。”這位學(xué)生說出了兩者表面上的區(qū)別，于是我又點(diǎn)名讓另一名學(xué)習(xí)較好的學(xué)生進(jìn)行補(bǔ)充，這位學(xué)生補(bǔ)充道：“兩者含有的未知數(shù)的項(xiàng)的次數(shù)都是1次的，并且二元一次方程組中的兩個(gè)方程的未知數(shù)相同。”通過這種提問方式先讓學(xué)習(xí)較差的學(xué)生回答問題，再讓學(xué)習(xí)較好的同學(xué)進(jìn)行補(bǔ)充，既照顧到了不同層次的學(xué)生，同時(shí)也實(shí)現(xiàn)了師生之間、學(xué)生之間的多維良性互動，讓學(xué)生對二元一次方程及二元一次方程組的區(qū)別與聯(lián)系有了更加深刻的認(rèn)識。

老師在進(jìn)行提問時(shí)不可以只以學(xué)習(xí)好的學(xué)生為中心而忽略了其他學(xué)生，老師在設(shè)置問題時(shí)也要考慮到學(xué)生的學(xué)習(xí)情況，有指向性地進(jìn)行提問。

二、內(nèi)化邏輯，相互呼應(yīng)

課堂上留給老師講課的時(shí)間非常少，而老師想要充分利用這短短的45分鐘讓學(xué)生學(xué)到更多的知識，提升課堂效率和教學(xué)質(zhì)量，還需要在設(shè)置問題時(shí)注意問題之間的內(nèi)在邏輯，從而讓學(xué)生在問題的引領(lǐng)下對數(shù)學(xué)知識逐步進(jìn)行了解，對知識重難點(diǎn)進(jìn)行突破。

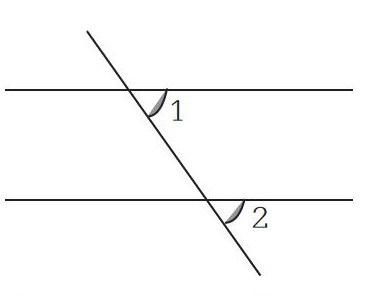
例如，我在給學(xué)生們講解平行線的判定這一節(jié)內(nèi)容時(shí)，在講解“同位角相等，兩直線平行”這一定理時(shí)，我先利用三角板和直尺在黑板上為學(xué)生們展示了平行線的畫法（如右圖）。我在畫完兩條平行線之后向?qū)W生們提問：“我在畫圖過程中，你們看到什么角始終是相等的啊？”學(xué)生們回答：“角1和角2始終相等。”于是我接著問第二個(gè)問題：“那角1和角2是什么角啊？”學(xué)生們回答：“它們是同位角。”此時(shí)學(xué)生們已然明白兩條直線被第三條直線所截，如果它們的同位角是相等的，則可以判定兩條直線是平行的。通過設(shè)置這種具有邏輯關(guān)系的問題，學(xué)生們一步步了解了判定平行的這一定理。

學(xué)生對數(shù)學(xué)問題的認(rèn)識是存在一定的邏輯關(guān)系的，老師要結(jié)合這種邏輯關(guān)系來設(shè)置問題，使得設(shè)置的問題能夠前后呼應(yīng)，這樣才可以節(jié)約課堂時(shí)間，讓學(xué)生學(xué)習(xí)到更多的知識。

三、適時(shí)追問，完善結(jié)構(gòu)

我們講老師設(shè)置問題要具有藝術(shù)，而老師何時(shí)對學(xué)生進(jìn)行提問也是一種藝術(shù)。如果老師的問題切入時(shí)間不對，不但會打亂課堂節(jié)奏，同樣也會使得課堂效率下降，如果老師能夠適時(shí)對學(xué)生提問，不僅能夠?qū)W(xué)生有所啟發(fā)，同樣也會使得學(xué)生的知識結(jié)構(gòu)有所完善，提升教學(xué)質(zhì)量。

例如，有一次我讓一位學(xué)習(xí)比較差的學(xué)生回答菱形是不是平行四邊形時(shí)，這位學(xué)生有所猶豫，于是我就先問他還記不記得平行四邊形的判定定理，這位同學(xué)思考了一會，將平行四邊形的判定定理講了出來，于是我就追問到：“菱形的兩組對邊分別相等嗎？”他回答：“相等。”我接著又問他：“菱形的一組對邊相等且平行嗎？”他也回答：“是的。”這時(shí)我就問他：“現(xiàn)在知不知道菱形是不是平行四邊形了？”他回答：“知道了。”通過適時(shí)追問，這位學(xué)生完善了對平行四邊形判定定理的認(rèn)識，也知道了菱形是特殊的平行四邊形。

老師進(jìn)行適時(shí)追問，給學(xué)生以啟發(fā)，而不是直接告訴學(xué)生答案，這樣既可以幫助學(xué)生思考問題，也完善了學(xué)生的知識結(jié)構(gòu)。

“集約型”課堂備受矚目，其目標(biāo)是利用有限的教學(xué)時(shí)間及資料讓學(xué)生取得最好的學(xué)習(xí)成果，如果老師能夠合理運(yùn)用提問這門藝術(shù)，必將提升數(shù)學(xué)課堂的教學(xué)效率，構(gòu)建高效的集約型課堂。