借助“示錯”策略 優化概念教學

余靜

摘? 要：概念教學是小學數學教學中的重點內容，小學生在學習數學概念的過程中經常會出現認知上的錯誤，這種錯誤是一種有效的教學資源。借助“示錯”策略能夠有效地優化小學生的概念學習。基于此背景，本文對引入概念時“示錯”，強化概念感知;形成概念時“示錯”，促進概念形成;鞏固概念時“示錯”，深化概念理解的策略進行了探究，希望能達到一定的借鑒意義。

關鍵詞：概念教學;數學概念;示錯

在小學數學知識體系中，數學概念是重要的組成部分，也是重點教學內容，因為小學生要想系統地學好數學知識，就必須先理解數學概念才能實現。數學概念具有抽象化的特征，小學生有關數學的“前概念”或負遷移等都會對數學概念的理解產生影響，從而出現偏差。《數學課程標準》強調教師在開展教學時，要以學生已有的知識經驗為基礎。小學生對數學概念的理解往往會存在錯誤，在小學數學概念教學中，教師要大膽地把學生的錯誤展示出來，并以此為教學資源引導學生進行深入學習，以便學生在觀察和思考錯誤中實現有效反思和探究，從而達到概念學習的高效化。

一、引入概念時“示錯”——強化概念感知

小學生的生活經驗會讓他們對數學概念的理解產生一定的影響，在對一些數學概念的感性認識上，往往有一些錯誤的認知。教學中，教師有必要直面學生的錯誤，通過主動示錯的策略強化他們對正確數學概念的感知。

例如，一位教師在教學《平行四邊形的面積》一課時，有這樣一個教學片段：

師：今天我們要學的內容是“平行四邊形的面積”（邊說邊板書）。請大家看大屏幕，有一個底為8厘米，側邊長為5厘米的平行四邊形，這個平行四邊形的面積有多大？（多媒體展示所描述的平行四邊形）

生：面積應該為40平方厘米。

師：能說說你怎么算出來的嗎？

生：由8×5=40得到的。

師：這樣算的原因是什么？

生：我從長方形面積計算公式得到的啟發，用“底×邊”來計算平行四邊形的面積。

師：好像說得也不錯。那請大家利用格子圖來對其面積大小進行驗證好嗎？（邊說邊拿出格子圖，并把圖形置于其中）

師：請大家數數看，它的面積是40平方厘米嗎？

（學生數格子后得出其面積大小為32平方厘米，于是引起了討論。）

生：這個面積不是40平方厘米，說明剛剛采用的計算面積的方法不對。

以上教學片段中，學生利用了“前概念”——長方形的面積計算方法來類比平行四邊形，出現了錯誤。而教師主動利用了學生的感知錯誤，及時讓學生在自主探究中糾正其“負遷移”，讓學生的探究熱情越發高漲。在此基礎上，學生進行的探究活動必然是高效的，有利于有效建構其有關平行四邊形面積計算的本質特征。

二、形成概念時“示錯”——促進概念形成

在小學數學概念教學中，促進學生形成數學概念是教學的重點。而很多無關緊要的因素會影響到學生理解數學概念的準確性，進而出現偏差。為此，這些偏差就應被主動地呈現于學生眼前，讓學生投入對自身思考結果的反思中，促使他們更深入地理解概念的本質規律。

（一）借助“示錯”，把握概念要素

小學生處于思維發展階段，因而思維缺乏嚴密性，這讓他們很難對相關概念的關鍵點進行準確的把握，以致出現一些錯誤的理解。為了讓學生對概念的不同要素有更清晰的把握，教師可通過“示錯”的方式來進行概念教學。

例如，一位教師在教學《角的認識》一課時，有這樣一個教學片段：

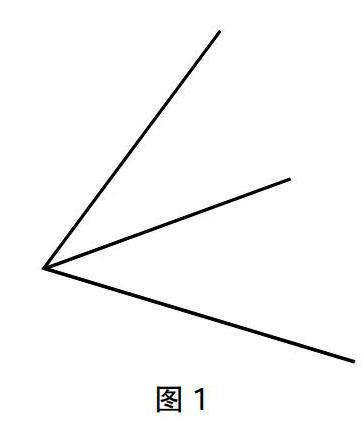
師：從前面的學習中，我們了解到角是由一個頂點和兩條邊組成的。那么，請觀察如下圖形，數一數角有多少個？（圖1）

生：一共是2個角。

師：請同意他說法的同學舉手示意。

（很多學生紛紛舉起手來。）

師：那現在請一個同學上講臺告訴我們有哪兩個角好嗎？

（學生在指的過程中發現自己在觀察時忽略了一個角。）

生：老師，這里一共是3個角，剛才數錯了。

師：多的那個角在哪里呢？

生：這外面的頂點和由其出發的兩條邊也能形成一個角。

師：也就是說，在觀察角的組成時，只要能找到一個頂點和由其出發的兩條邊，就可以說它是一個角。那大家再數數這個圖形里的角的個數吧。

以上教學片段中，學生只從表面觀察了數學角，所以一開始只找出了兩個，教師則讓學生在指明角的過程中去發現錯誤并數出正確的個數。學生通過細數意識到自己的認識錯誤，從而更深刻地理解了角的“一個頂點和兩條邊”的組成概念。

（二）借助“示錯”，引導概念辨析

小學生在學習數學概念的過程中往往會存在表面化的現象，教師要借助“示借”策略，引導學生進行概念辨析。

例如，一位教師在教學《軸對稱圖形》一課時，有這樣一個教學片段：

師：我們剛剛對軸對稱圖形的概念進行了學習。那請大家對屏幕上所展示的一系列圖形進行觀察，判斷它們是否屬于軸對稱圖形？（邊說邊在屏幕上放出正方形、平行四邊形、三角形和圓）

（對于平行四邊形是否為軸對稱圖形，學生們持有不同的意見。教師抓住這一契機引導學生進行辯論賽。）

生1（正方）：我方認為，平行四邊形屬于軸對稱圖形，我們可以沿其中間剪成兩部分，所得兩部分一模一樣。

生2（反方）：我方認為這種說法是錯誤的。雖然兩邊完全一樣，但沿中間對折后，平行四邊形的兩邊是無法重合在一起的。

生3（正方）：請看我的操作，先用剪刀沿其中間剪成兩部分，然后觀察發現兩邊是一樣的圖形，所以它屬于軸對稱圖形。

生4（反方）：你用裁剪的方式得到的結論是不對的，應該通過對折看其是否重合。

（生1聽后開始對折平行四邊形，發現不管怎樣都無法保證兩邊是重合的。）

生1（正方）：是我理解錯了。要讓平行四邊形沿中間分開的兩部分能重合，不能通過對折來實現，而必須要用裁剪的方式才能做到，這和軸對稱圖形的定義是不相符的。

以上教學片段中，教師巧妙地抓住了學生的思維錯誤，引導學生通過辯論的形式來加深對“軸對稱圖形經過對折，能讓兩邊重合在一起”的理解，推動學生對軸對稱圖形概念的準確把握。

三、鞏固概念時“示錯”——深化概念理解

除了讓學生學習新的數學概念，還應及時地進行鞏固，這也是非常關鍵的。教師在組織學生鞏固概念時，應主動呈現出學生所犯的錯誤，從而糾正學生的思維，加深已掌握數學概念的印象。

（一）借助“示錯”，理解概念本質

教師對小學生開展概念教學時，應注重引導學生把握概念的本質特點。為此，可通過“示錯”的方式來達到這一目標。

例如，一位教師在教學《認識分數》一課時，有這樣一個教學片段：

師：請大家觀察，用“1/2”來表示下圖的涂色部分正確嗎？（圖2）

生：是錯的。涂色和不涂色兩部分是不相等的。

師：那能否用所學的分數來表示其涂色部分呢？

生1：不行。

生2：我同意。這個圖形的分割方式不是平均的，所以無法用分數對其進行表示。

師：那我現在再為它添上兩條線，大家再觀察一下，想一想可否用分數對涂色部分進行表示？

生3：這樣劃分之后就可以用“1/2”來表示它。

師：為什么這樣就可以呀？

生3：因為加了兩條線后，整個三角形被均分為4份，而有一份被涂上了顏色。

生4：我明白了，今后遇到類似的問題，我們應該從不同的角度去觀察其分割方式是否為平均的。

生5：從這個題中我們也可以明白，在觀察圖形時，常常會出現表面看上去未平均分的現象，但通過深入觀察和分析后，仍可得出其是平均分的。

以上教學片段中，教師沒有避開學生因思考缺乏周密性而出現的錯誤，而是引導學生去發現思維錯誤，進而讓他們體會到圖形的均分與否僅從表面去觀察是不對的，應該深入圖形特征進行分析和思考，從而揭示出圖形平均分的份數，確定用哪個分數進行表示。這對強化學生理解分數概念的程度具有重要意義。

（二）借助“示錯”，理解概念內涵

對于數學概念內涵的深刻理解，教師也應用“示錯”的方式來開展概念的教學，以實現更加高效的概念學習。

例如，一位教師在教學《等腰三角形》一課時，有這樣一個教學片段：

教師為學生設計如下題目：有一個等腰三角形，其三條邊中有兩條邊已知，分別是2cm和5cm，那么，請問其周長為多少？

生1：假如5cm的邊為它的腰，那么周長等于5+5+2=12cm。

生2：假如2cm的邊為它的腰，那么周長等于5+2+2=9cm。

師：請大家把題目所描述的三角形

畫在草稿本上好嗎？

（學生著手繪制三角形，教師讓學生表達自己的想法。）

生2：老師，我剛剛的回答是錯的。因為如果腰長為2cm，那么兩腰的和小于第三條邊。

生3：我同意，因為2+2<5，而三角形任意兩邊的和應該大于第三邊。

生4：雖然等腰三角形不是普通的三角形，但它同樣要符合一般三角形的基本規律，我們要注意題目給我們挖的陷阱。

學生在學習等腰三角形時，往往只注意保證其兩條腰的長度一致。而在上述教學片段中，教師從學生的錯誤點著手，讓學生自行繪制自己得到的等腰三角形，這樣學生通過動手操作發現腰為2cm時不能形成三角形，這對學生鞏固已學的三邊規律的知識有著重要的作用。

綜上所述，把“示錯”策略引入概念教學之中，能有效地把握學生理解概念時的偏差原因。同時，把“錯誤”展示出來，還有利于學生思維的活躍，讓他們在學習數學概念時實現更高的效率。