由“聚”到“散”，提升核心運算能力

【摘要】《義務教育數學課程標準（2011年版）》中將“運算能力”作為十大核心概念之一，強調理解運算的算理，并尋求合理簡潔的運算途徑解決問題。對于運算律和運算性質的總復習教學，需要通過對運算律、性質的“聚合”及在解決問題中“發散”運用，深入挖掘運算律、運算性質的本質特征及其相通之處，提升學生的核心運算能力。

【關鍵詞】小學數學；聚合；發散；運算能力

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2017）49-0041-04

【作者簡介】董良，蘇州大學實驗學校（蘇州，215133）教師，高級教師，蘇州市雙十佳青年教師，蘇州市小學數學兼職教研員。

運算能力是《義務教育數學課程標準（2011年版）》在修訂過后增加的十個核心概念之一，也是作為三種基本數學能力之一（還包括空間想象能力和邏輯思維能力——林崇德語），對數學學習來說起到了基石性的作用。沒有運算能力的支撐，不可能學好數學。《義務教育數學課程標準（2011年版）》也指出：“培養運算能力有助于學生理解運算的算理，尋求合理簡潔的運算途徑解決問題。”運算能力是運算技能與數學思維的結合，主要指能夠根據概念、公式、法則、定理等對題目進行正確的運算，及在理解運算算理的基礎上，能夠借助數學思想方法，尋求合理的運算途徑，并可以靈活地解決問題。

作為畢業階段的計算總復習教學，如何在學生已有的六年計算技能的基礎上，進一步做到理解運算的算理，正確地進行運算，同時在運算的過程中更加合理地運算、簡潔地運算，筆者試以六年級下冊“運算律和運算性質總復習”的教學片段為例，對復習課培養核心運算能力進行探討。

一、聚——溝通聯系，凸現運算律本質特征

這里的“聚”是將小學階段所學過的各個運算定理和性質整合在一起，經過抽象整理，進行系統梳理，讓學生能夠深入地挖掘出運算定律、運算性質的本質特征及其相通之處，為接下來合理、靈活地通過運算解決問題找到充分的理論根據。

請看下面的教學片段：

師：我們都學過了哪些運算定律，你能用字母表示出來嗎？

學生回答，教師根據學生的回答相機用磁性卡片貼出。

師：看著這些字母表達式，你能試著說說它們分別表示什么意思嗎？

先同桌討論，再全班交流。

師：如果請你給它們分類，你準備怎樣分？小組內討論。

生：分成加法和乘法兩大類。

師（根據學生的回答調整卡片的位置）：說說你的依據。

生：分成三類，交換律、結合律和分配律。

根據學生的回答重新調整卡片的位置。

師：誰能說說看，交換律有什么特點？（變的是數的位置，不變的是計算結果。）

師在交換律的左邊板書：位置改變。

師：結合律有什么特點？（變的是運算順序，不變的是計算結果。）

師在結合律左邊板書：運算順序改變。

師：乘法分配律有什么特點？（變的是計算的方法，不變的是計算結果。）

師在分配律左邊板書：計算方法改變。

師：這里的計算方法怎么改變啦？

生：可以先求積，再求和；也可以先求兩個不同乘數的和，再求積。

師：老師發現，同學們所說的運算律都是加法和乘法的，那減法和除法有沒有呢？

生：減法和除法有運算性質。

師：誰能用字母表示減法和除法的運算性質？

生回答，師相機卡片貼出。

師：看著字母表達式，能給大家解釋一下嗎？

生舉例說明。

師：學了這么多的運算律和運算性質，你覺得最大的好處是什么呢？（使計算簡便。）

板書：計算簡便

師：為什么可以利用它們來進行簡便計算呢？

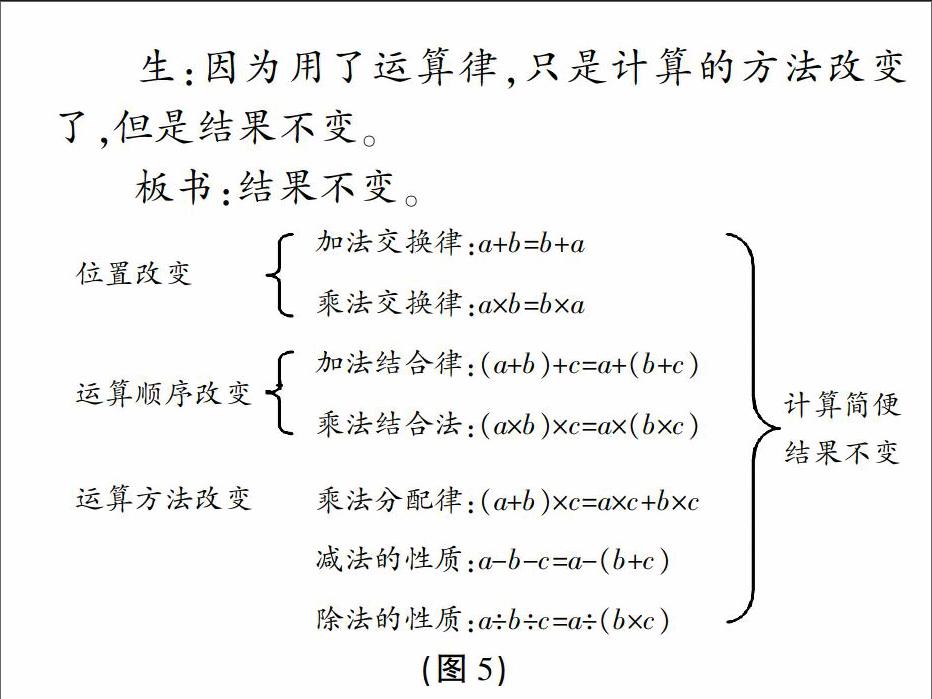
生：因為用了運算律，只是計算的方法改變了，但是結果不變。

板書：結果不變。

針對六年級的學生已經具備了一定的歸納整理能力這一特點，教師并沒有簡單地羅列各個知識點，而是引導學生通過觀察、思考、交流，找出各部分內容之間的關系或蘊藏的規律，建立良好的認知結構。教師先讓學生回憶學習過的運算定律，接著讓學生試著將學過的運算定律進行分類，并說出這樣分類的依據，尋找各自的特點，從而溝通各運算定律之間的聯系，并由“加法、乘法”引申到“減法、除法”，接著回顧整理運算性質，最后通過討論、交流，學生總結得出結論：學習了運算定律和運算性質，可以在計算結果不變的情況下，使計算變得簡便。從而將各個知識點連接起來，形成一個系統的，有聯系的，有結構的知識網絡。在這個過程中，教師給了學生足夠的時間、空間，讓學生創造性地完成知識結構與認知結構的構建。

二、散——拓展應用，提升核心運算能力

曹才翰先生在《中國中學教學百科全書（數學卷）》中指出，運算能力并非一種單一的數學能力，它是運算技能與邏輯思維能力的一種獨特結合。學生運算能力的發展主要通過數學解題活動來實現。學生的運算能力主要表現為能正確、迅速的感知題目形式，確定題目類型，根據題目類型選擇解題模式、解題方法，然后多方向地尋求解題方法，擺脫思維定式，力求解法簡潔合理，并對題目類型、解題模式方法進行反思總結概括等。

經過前面的抽象整理，接下來則需要從練習設計中放大核心知識，才能體現知識的連貫性，經歷抽象整理、拓展應用的過程，體現了復習課中對已學知識的“聚合”和在應用知識中“發散”的功能與特征。

接著看下面的練習教學片段：

第一關：仔細審題，怎樣簡便就怎樣算。

師：我們在做題之前，一定要先看清題目的要求，誰來讀一下這里的題目要求，要讀得有水平！endprint

師：你是怎么理解這個要求的？

生：就是要靈活選擇合適的方法來計算。

師：那好，我們就按照這樣的要求再來練幾題。（出示課件）

×100 125×8.8

×+× （+）×

生在作業紙上完成，集體反饋。

課件出示：×100=

師：這樣做的舉手？（少數學生舉手，大多數學生對比屏幕后恍然大悟。）

出示：×100=×（99+1）=×99+=7+=7

師：是這樣做的舉手？（大部分學生無奈地舉手） 師：覺得哪種方法更簡便？

生：第一種。

課件出示：

師：有不同的做法嗎？

學生答，課件出示：

師：有什么想說的嗎？

生：125×8.8既可以用分配律，也可用結合律。

課件出示：

師：比較一下這一題的兩種方法，發現什么？

生：既可以用分配律，也可以直接約分，先算乘法，再算加法。

師：發現什么了？

生：用了乘法分配律，反而不簡便了。

師：現在讓我們再觀察一下這4道題，有什么感想，想和大家交流？

生：我理解了什么是“怎樣簡便就怎樣算”，我覺得做題的時候一定要根據實際情況選擇合適的方法，有的時候不運用運算律，反而會更簡便。

第二關：自己來編題，在括號里填數，運用運算律和運算性質讓計算簡便。

125×15×（ ） ×+×

師：先獨立思考，再在小組里交流。

生：第1題可以填8，16，32，……

生：第2題我填的是×，這樣就可以用乘法分配律，等于×（+）。

生：我覺得還可以填×，運用乘法分配律，等于（+）×。

解決問題時運算方法合理、簡潔是運算能力較高的要求。但事實上，許多學生在運用運算律和運算性質時，往往流于僵化，主要體現在三點：（1）運用運算定律和運算性質計算時思維定式嚴重，常囿于一種思路和方法，不愿意思考是否可以運用多種運算定律或性質進行計算。（2）面對“能簡便計算的要簡便計算”時，學生能意識到要運用運算定律進行簡便計算，面對其他情況下則無此意識。（3）對于“怎樣簡便就怎樣算”，理解成了一定要運用各種運算定律和運算性質進行計算，不會靈活地選擇計算方法。教師在這里的處理是獨具匠心的，各種“陷阱”，學生屢屢中招，才能在計算、交流、辨析中提升對“怎樣簡便就怎樣計算”的理解。不僅如此，教師還關注后續學習，拓展思維深度。讓學生根據運算律和運算性質改編或自編習題。這樣先“聚合”再“發散”的處理，體現了復習課中特別是畢業班復習教學的基本要求與策略，讓學生的學習真實發生，真正提升了核心素養的運算能力。

當然，運算能力的培養與發展是一個長期的過程，應伴隨數學知識的積累而淡化。運算能力的培養與發展不僅包括運算技能的逐步提高，還應包括思維素質的提升和發展，真正把“運算能力”作為數學核心素養，就要從純粹計算的外表進入到學生思維的核心，從教師的說教牽引向學生自我醒悟的核心，從能算、會算發展到合理的算、簡潔的算的核心。這是運算教學的至高追求。

【參考文獻】

[1]湯衛紅.基于核心素養的運算能力及其培養[J].福建教育，2016（Z5）：96-99.

[2]陳文梅.數學核心素養之運算能力的培養[J].小學數學教育，2016（Z3）：41-46.endprint