追問初中學生對概念的類比

江勤娟

[摘 要] 數學思想是數學學習的精華部分，學生對數學思想的領悟直接決定著其數學學習的效果和應用數學的能力. 為此，在常態化的數學教學過程中，教師要注重數學思想的滲透和引領.

[關鍵詞] 類比；數學教學；追問；概念教學

類比思想是數學中的重要思想，是解決新問題和學習新知識常用的策略，通過運用已有的知識經驗，將新的問題與原有問題進行比較，找到它們的相似或相通之處，從而創造性地解決新問題. 讓學生領會類比的思想，學會用類比思想解決學習中的問題，對提高教學效率有積極的作用. 下文筆者以“二次函數”第一課時的教學片段為例，就類比思想在教學中的滲透談談自己的看法.

獨學思考，提出問題

新課程改革的最大呼吁就是將課堂還給學生，把學習的自主權還給學生. 因此，讓學生獨立思考，提出疑問，可以有效地讓學生的注意力集中到課堂中，激發學生的學習欲望，啟發學生的思維、引領思維的方向.

完成方式：學生獨立快速閱讀課本相應內容，了解本節課所學內容，并列出本節課想獲取的知識或想解答的問題，隨后全班展示問題.

教師通過對學生所提的問題進行歸類、匯總，整理出具有代表性和討論價值的問題，作為“智慧問題”滲透于課堂中共同探討解決. 本節課學生提出的智慧問題如下：

①二次函數學什么，難不難？

②什么樣的函數叫二次函數？

③y=（x+1）2-（x-1）2和y=是二次函數嗎？

④二次函數y=ax2+bx+c中為什么a≠0？b=0可以嗎？

⑤學習二次函數有什么用？

⑥二次函數的自變量x有范圍嗎？函數值y能等于0嗎？

⑦二次函數y=ax2+bx+c的解析式中需要幾個條件才能求出a，b，c的值？

⑧做二次函數的題目有哪些技巧經驗？

二次函數是初中階段的重點和難點，本節課是二次函數的起始課，正確有效地引導，讓學生對本章內容產生興趣是章節起始課的教學目標，也是二次函數第一課時的教學目標. 在此之前學生已學過一次函數，通過類比思想，能對二次函數有初步的認識. 通過質疑提問，一方面可以激發學生對本節課內容的探索欲望，另一方面學生也因為一次函數的回顧而對二次函數的學習充滿信心和親切感，提升學習的親和力.

類比舊知，引入新知

類比思想是初中生學習概念的主要依托和方法，通過類比舊知，學生可以重新認識舊知，并在教師的指導下用類比的思想認識新知，無形之中達成對新概念的理解與知識的建構. 二次函數的概念可以通過與一次函數概念的類比推導出來，因此讓學生先從解析式的聯系中感受二次函數與一次函數的聯系與區別.

①已知摩托車的速度為60 km/h，則總路程s與時間t的函數關系式為______.

②一只烏龜掉進了5米深的井底后沿著井壁往上爬，已知它每分鐘爬0.5 m，則剩余的路程s（m）與烏龜爬行的時間x（min）之間的函數解析式為______.

③小明每天早上勻速跑步去學校，已知他家離學校3000 m，則他上學所用的時間t與速度v的函數關系式為______.

④圓的面積S與半徑r之間的函數關系式為______.

⑤已知菱形的兩條對角線的和為24 cm，設其中一條對角線的長為x cm，則菱形的面積S（cm2）與x（cm）之間的函數解析式為______.

⑥某種產品現在的年產量是20 t，計劃今后兩年增加產量. 如果每年都比上一年的產量增加x倍，那么兩年后這種產品的產量y為______.

完成方式：學生獨立完成，后全班交流展示.

學生得到了以下答案：①s=60t，②s=5-0.5x，③t=，④S=πr2，⑤S= -x2+12x，⑥y=20（1+x）2=20x2+40x+20.

問題1：你能對上述六個解析式進行分類嗎？分類的標準是什么？

問題2：你能類比一次函數的概念對二次函數下定義嗎？

師生共同揭示定義：形如y=ax2+bx+c（a≠0）的函數叫作二次函數，其中a是二次項系數，b是一次項系數，c是常數項.

問題3：指出④⑤⑥中的二次項系數、一次項系數、常數項.

問題4：解決智慧問題①②③，強調判定二次函數的方法.

二次函數的概念是本節的重點內容，讓學生通過觀察不同類型的函數解析式，類比一次函數的定義，自己對二次函數下定義，有比較地理解二次函數的概念，感知類比思想.

運用新知，展示才智

新知的運用是每節課的重要環節，一方面通過對所學知識的運用，可以加深學生對概念的理解，使知識掌握更牢固；另一方面，因課堂是一個展示的平臺，通過問題的解決可以為學生提供展示的機會. 其實在展示的過程中，學生也會發現很多地方都有異曲同工之妙，即應用之中也有類比思想.

問題1：函數y=ax2+bx+c（其中a，b，c為常數），當a，b，c滿足什么條件時，（1）它是二次函數？（2）它是一次函數？（3）它是正比例函數？

通過該問題，讓學生厘清各項系數與函數類型的關系，掌握正比例函數、一次函數、二次函數之間的關系，從而對二次函數中二次項系數a≠0加深印象.

問題2：若函數y=（m2-1）xm2-m為二次函數，求m的值.

題后反思：你覺得這個問題中容易出錯的地方在哪里？（易忽視m2-1≠0）

你能總結這類問題的解題經驗嗎？（①討論次數，②討論二次項系數）

該問題是考查二次函數概念的常見題，學生往往只考慮到了次數，容易忽視二次項系數不為0這種情況，所以作為例題共同討論、并總結做題思路與解題經驗，可以在一定程度上讓學生避免類似錯誤再次發生，培養他們考慮數學問題的嚴謹態度.

再解決智慧問題④，理解二次函數的實質.

內化知識，總結經驗

學生是知識的接收者，教學的目的是為了讓學生將所學內容內化為自己的知識，建構自己的知識體系，總結規律、形成方法. 總結經驗是促進知識內化的有效途徑與方法.

解決智慧問題⑤，學習是為了服務于生活，學習數學是為了更好地服務生活，用二次函數解決實際問題即是函數的“用處”.

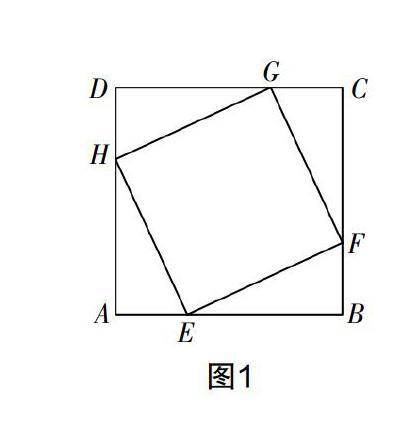
例1 如圖1，一張正方形紙板的邊長為2 cm，將它剪去4個全等的直角三角形，設AE=BF=CG=DH=x（cm），四邊形EFGH的面積為y（cm2），求：（1）y關于x的函數解析式和自變量的取值范圍. （2）當x分別為0.25，0.5，1，1.5，1.75時，對應的四邊形EFGH的面積，并列表表示.

在問題（1）中，易證四邊形EFGH為正方形，學生們發揮才智，共想出了4種解答方法. 方法1是先表示出邊長，再平方求面積；方法2是用面積的和差，將四邊形EFGH的面積轉化為正方形ABCD的面積與四個三角形面積之差；方法3是連接HF，將正方形ABCD分割為兩個梯形，再用面積和差算出△HGF的面積，兩倍即為四邊形EFGH的面積；方法4是過H，G分別作與正方形ABCD的邊平行的線段，將圖形分割來求. 這四種方法雖然繁簡不一，但都體現了學生們積極思考、樂于動腦的精神，教師要對此進行肯定，有利于學生們發散思維的訓練. 以該問題為例，解決智慧問題⑥，讓學生知道函數自變量的取值范圍與實際問題的關系.

問題（2）的表格如下：

從表格中引導學生們發現二次函數的對稱性、增減性、最值，為下一節課的內容做好準備.

例2 已知二次函數y=x2+px+q，當x=1時，函數值為4；當x=2時，函數值為5，求這個二次函數的解析式.

師：如果將解析式變成y=ax2+px+q，其余條件不變，你還能求出它的解析式嗎？

生：不能.

師（追問）：那需要增加怎樣的條件才可以求出呢？

生：再增加一個點.

變式：已知二次函數y=ax2+bx+c，當x=1時，y=2；當x=-2時，y=-7；當x=-1時，y=0，求這個二次函數的解析式.

題后反思：解決智慧問題⑦，掌握待定系數法求二次函數解析式的方法.

師：類比一次函數解析式的求法，你能總結二次函數解析式的求法嗎？

生：待定系數法，解析式中有幾個未知字母就需要幾個點.

這兩個問題是用待定系數法求解析式的基本問題，由例2到變式的過渡是為了讓學生感悟“求幾個未知數就需要幾個方程”的思想在這里的遷移，從而更清楚地知道求解析式需要的對應點的個數.

解決智慧問題⑧，師生共同總結本節課所學的內容及實際問題的答題技巧.

二次函數是初中數學代數的重點和難點，第一課的概念教學對整章的教學有著奠基作用. 函數本身就是較抽象的內容，學生不易理解，類比一次函數，可以讓學生有參照，找到熟悉感，從而對學好本章內容樹立信心. 在教學中，教師的關注點應是學生對二次函數與一次函數之間關系的理解及類比思想的掌握與應用.

類比思想是初中階段的重要思想，籠統地來說，解決一切新的問題都是在已知問題和已知方法的前提和基礎上進行的. 因此，在數學教學中滲透類比思想，尤其是概念的類比，不僅可以讓學生學會知識的遷移，而且在此基礎上學會方法的類比也可以讓學生感知解決問題的基本思路，提高學習效率.