智慧課堂下的智慧

董兆國

【摘要】在初中數學教學中培養學生的創新性思維，應注意為學生的“收斂思維與發散思維”“邏輯思維與非邏輯思維”提供問題情境和恰當的活動形式。近幾年在互聯網+時代下的智慧課堂引導下，作者也在平面幾何課堂中通過幾個方面的訓練來培養學生的創新思維，即利用“一題多解” “一題多變”“一圖多用”“一圖多變”的訓練來培養學生的創新思維。

【關鍵詞】 平面幾何課堂；創新思維；培養

所謂數學創新性思維，是指思維的結果或處理問題的方法帶有新穎性，獨特性。從思維過程的狀態來看，創新性思維在總體上是表現為：……→收斂思維→發散思維→收斂思維→……發散以便于聯想，尋找各種“舊”知識之間可能的“新”組合，發現推理的起點。從思維的邏輯形式來看，數學創新性思維中既含有邏輯思維的成分，也含有直覺思維的成分。在初中數學教學中培養學生的創新性思維，應注意為學生的“收斂思維與發散思維”“邏輯思維與非邏輯思維”提供問題情境和恰當的活動形式。

時代在發展，現在的課堂已經不再像過去老師講，學生聽，而是進入了“互聯網+”時代的智慧課堂，學生開始主動學習。“互聯網+”時代的智慧課堂包括學生個性學習、學生之間互動學習、移動學習、網絡學習等，讓學習有效果，成績有提高；教師高效教學，課前認真備課、預設問題，課中參與學生學習，課后總結反思等創新教與學模式，減輕教師負擔，把教師從煩瑣的事務解放出來。學生知識的獲得也不是單一通過課堂，而是多方位，多角度。社會發展，人才競爭，都呼喚創新型的人才。教師是創新型人才的直接培養者，在教學中應注重啟發和培養學生的創新思維，發展他們的創新才能。新課程標準也要求教師是學生學習的組織者和合作者，是學生的學習伙伴。老師要將課堂退還給學生，讓學生自主學習，去爭議，去討論，去發現。有些老師認為，新課標下的初中幾何對學生要求低，達不到訓練學生創新思維的目的。其實許多幾何題具有代表性和典型性，教師在教學中要教會學生去挖掘題中的潛在內涵和外延，讓學生學會在學數學的基礎上去做數學，感悟數學，這樣不僅可以培養學生的創新思維，更能教會學生愛創新、敢創新的好品德。在多年的數學教學中，尤其近幾年在互聯網+時代下的智慧課堂，讓我對平面幾何教學中充分發揮學生的創新思維有了新的認識。下面從本人課堂的幾個片段去淺談如何培養學生的創新思維。

一、利用“一題多解”的訓練來培養學生的創新思維

對于一道能用幾種解法的題目，應該鼓勵學生用不同的思維方式，從不同的思維角度去尋找多種解題的方法，這樣不僅有利于培養學生靈活運用知識的能力，而且有助于培養學生發散思維。

【例1】如圖，已知：點D在AB上，點E在AC上，BE和CD相交于點O，AB=AC， ∠B=∠C.求證：BO=CO.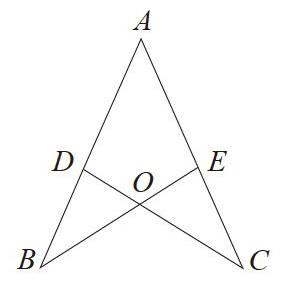

本題是在全等三角形的復習課上出現的例題，題目剛出現就有一個同學甲說：“連接AO，因為AB=AC，∠B=∠C，AO=AO，所以可證ΔABO≌ΔACO。”這個同學剛說完就有另一個學生乙提出：“這兩個三角形不全等。”“全等。”其他同學大聲地喊道。這時班里的同學們像炸開了鍋，爭得面紅耳赤。就在這時，同學丙站起來說：“這兩個三角形是全等的，但是它們不能用連接AO直接證明全等，因為我們是用‘邊邊角的方法證明全等，這顯然是錯誤的……”這時大多數同學才醒悟，明白先證ΔABE≌ΔACD得AD=CE，再進一步證ΔBOD≌ΔCOE，從而得BO=CO。我并沒有繼續追問，只是沉默了一會兒，突然有一個同學在下面喊起來：“連接BC，由AB=AC得∠ABC=∠ACB，又已知∠ABE=∠ACD，則∠OBC=∠OCB，所以OB=OC。”同學們聽完后報以熱烈的掌聲。通過這樣爭議、討論，同學們不僅清楚地知道證線段相等的方法，而且進一步掌握了用‘邊角邊證三角形全等的條件，同時也培養了學生的求異思維和創新的思維。

二、利用 “一題多變”的訓練來培養學生的創新思維

有些幾何題中，可以改變原題中某些條件，引出與原題相類似的題目，經過學生的鉆研，應用，從而加強此類題目的橫向和縱向聯系，能夠起到舉一反三、觸類旁通的效果，培養學生思維的變通性和準確性。如在原題中已知條件不變的情況下，深挖結論的多種形式和結論的延伸變化，從而開闊學生的解題途徑和方法，培養學生的發散思維，使其形成不斷探索問題的精神；把原題中圖形進行適當位置變化，而結論相似，從而使學生從圖形變化中概括總結出解題方法，培養學生思維的收斂性和流暢性等。

【例2】如圖①，已知△ABC中，∠BAC=90°，AB=AC，AE是過A的一條直線，且B、C在AE的異側，BD⊥AE于D，CE⊥AE于E.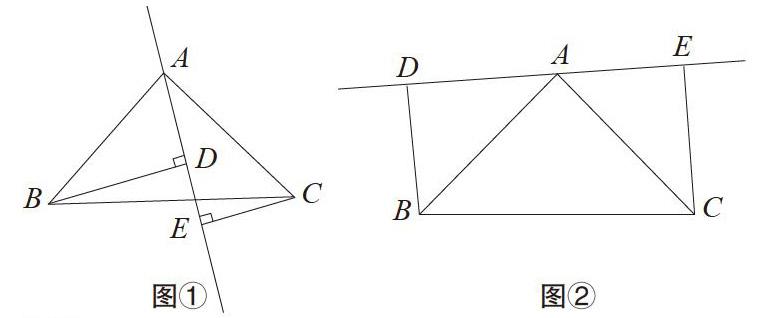

求證：BD=DE+CE

證明過程（略）

在同學們完成本題以后，我提出這樣一個問題：“請同學們認真讀題，能否只改變題中的某一個條件，得到與上題的類似的結論？”這是一個開放性問題，也比較難，學生沉默會兒，就主動進行小組合作學習，相互討論。有同學提出“將直線AE繞點A旋轉， 使點B、C在AE的同側，它的結論是BD=DE-CE”，如圖②。我讓他利用小平板拍照上傳展示了證明過程……在同學們的掌聲之后突然有一個學生提出：“老師，在旋轉過程中，結論在什么時候開始變化？旋轉前后的結論還有新的變化嗎？”“問得好，誰能回答這個問題？”經過同學們的再一番思考、討論得出了正確的結論。這種“問題學習”的數學教學方式既調動了學生學習數學的積極性和主動性，增強了學生參與數學活動的意識，又培養了學生動手實踐能力、觀察能力和自學能力，同時，也向學生滲透了“實踐—認識—再實踐—再認識”的辯證觀點，使學生充分感受到發現問題和解決問題帶來的愉悅，培養學生的數學創造性思維。這樣通過“一題多變”把所學的知識內容串在一起，達到融會貫通的目的，使學生學得自如，用得靈活，同時拓展了學生的解題思路，不斷發展學生的創新思維，從而提高學生解題能力和應變能力。

三、利用 “一圖多用”來培養學生的創新思維

幾何學是研究幾何圖形性質的科學，將某一些典型圖形剖析、挖掘、聯想、探討、完善圖形，可引出多種結論，由易到難，互相關聯，前一題為后一題論證，后一題應用前一題證得的結論，雖然有的難度較大，但受前一題的啟發也能化難為易，發展了學生應變能力和創新思維能力。

【例3】如圖，四邊形ABCD中，點E在邊CD上，連接AE、BE.給出下列五個關系式：①AD∥CB ②DE=CE ③∠1=∠2 ④∠3=∠4 ⑤AD+BC=AB，將其中的三個關系式作為題設，另外兩個作為結論，構成一個命題.

（1）用序號寫出一個真命題（書寫形式如：如果……那么……），并給出證明。

（2）用序號再寫出三個真命題（不要求證明）。

（3）加分題：真命題不止以上四個，想一想就能夠寫出幾個真命題，每多寫出一個真命題，就給你加1分。

這又是一道開放題，要求學生能夠準確地寫出真命題，尤其是第（3）小問難度較大。題中雖然沒有要求證明，但要寫出的是真命題，就要求學生知道它成立的理由，讓同學們在爭議中知道正確的答案。因此，利用“一圖多用”來引導學生挖掘題中條件與結論之間內界聯系，不僅培養學生聯想、探討、應變能力和創新思維能力，還能培養學生嚴密的邏輯思維能力。

四、利用“一圖多變”的訓練來培養學生的創新思維

初中幾何中的許多問題，大都在長期的歷史長河中，不斷地演變、引申、拓展，從而派生出現所謂“習題精華”“解題大全”，可你不可能嘗試所有題目，這就要求學生對某個題尋找解的過程中，總結、探索規律，引導學生正本清源、由表及里、顧次及彼，用心觀察，刨根究底，設疑解答，進行全方位的探求，去認識它的真面目，使學生活躍思想，開發智力，提高學生的解題能力。

【例4】如圖①，已知⊙A的半徑是2，⊙B與⊙A相內切，且⊙B經過A點，⊙A的弦CD切⊙B于E點，求圖中的陰影部分的面積.

解答（略）

在上述條件不變的情況下，如圖②，求圖中的陰影部分的面積。

（注意圖②與圖①的區別）

本題中求圖①的陰影部分面積較簡單，而要求圖②的陰影部分面積就比較困難，這就要求學生學會利用分割圖形求面積的方法，這里就不介紹具體的解法了。所以，利用“一圖多變”對題中的條件或結論進行演變、引申、拓展來訓練和培養學生的求異思維和創新思維有巨大的作用。

總之，創新思維的培養重在平時堅持，日積月累必將收到成效。師生都要樹立創新意識，教學中不要囿于參考書，要動手解題、動手編題，即使是成題，也要盡可能找出更好的解法教給學生，并指導學生也能想出更好的解法，師生都要做到在不疑處生疑，時刻樹立創新意識，讓學生天天都能有或大或小或多或少的創新，我們的教學便充滿生機與活力。同時在數學教學中，要注重拓寬學生的知識視野，發掘學生的好奇心，激發他們求知欲，啟發學生的創新思維，提高他們的創新能力，鼓勵他們創造發明，使他們都能成為我國科學技術現代化的后備人才，為更快更好地實現偉大復興的中國夢奠定人才基礎。