提高初中數學練習的有效性

劉振娟

[摘 要] 在初中數學教學過程中，練習是重要的組成部分. 在練習的過程中，教師要保證學生的主體地位，以各種教學素材為練習依據，結合教學目標，針對性地設計與布置練習. 本文以人教版初中數學為例，探討如何提高練習的有效性.

[關鍵詞] 初中數學；練習；有效性

練習是數學學習中不可缺少的，保證課堂教學高效性的重要措施就是設計有效的隨堂練習. 盡管如此，筆者結合現實教學過程中的所見所聞，發現部分課堂練習起不到應有的效果. 有的教師對課堂練習不夠重視，課堂內容講授完后就把時間交給學生自學，練習也只是按部就班，缺乏必要的設計與指導；有的教師鼓勵學生“刷題”，實施所謂的“題海戰術”，認為做得多了自然就理解了，缺乏目的性，效率低下，學生疲于應付，把練習當成硬性任務，逐漸喪失了學習熱情. 凡此種種，筆者結合一線教學經驗，談談對練習設計的一點思考.

目的要明確

在練習的設計過程中，教師要有明確的目標，對于需要學生掌握的知識，以及學生可能會遇到的問題，教師要有清晰的認識，進而按照自己的教學經驗對習題進行篩選，選出適合學生的、優質的練習. 此外，學生課后完成練習的時間比較有限，因此教師所設計的練習要有較強的針對性. 對于課程內容的重點與難點，要有直接的體現，這樣便于學生理解與掌握，便于提高學習效率.

案例1 如圖1，已知村莊A，B以及水站C，三地位于等邊三角形的三個頂點處. 由于旱季缺水，現需要從水站向兩村莊引水，請設計出最短的管道鋪設方案.

師：假設等邊三角形的邊長為a，請同學們設計出你們認為的最短路徑，并求解出相應的管道長度.

生1：管道就沿三角形的邊來鋪設，即鋪設線路為CA與CB（如圖2），管道長度為2a.

生2：過點C作CD⊥AB于點D，則管道鋪設線路為CD，DA與DB（如圖3），則管道總長度為a.

生3：作三邊的中垂線，交于點E，管道便沿著CE，EA，EB鋪設（如圖4），長度為a.

師：三位同學的方案都可行，綜合比較下來，生3的方法所鋪設的線路最短，在實際中能有效減少滲漏，節約工程造價，因此是最優方案.

評析 這樣的探究性練習以實際生活為背景，思路簡單，并不復雜，系統地考查了等邊三角形的性質、勾股定理以及實數的運算，涵蓋的知識點較多，同時貼近現實生活，能有效地引導學生將學到的數學理論與方法運用到實際問題解決當中，能極大地提升學生的學習熱情.

因此，數學練習的設計要帶有一定的目的性，要么是對概念或定理的擴展，要么是對數學思維方式與方法技巧的訓練或深化. 如果只是按照教輔資料去布置作業，去安排練習，那教師不會了解學生真正需要的是什么，不知道哪些內容是學生真正需要進行練習與強化的，會使得數學練習極為機械，缺乏目標，時間一長，學生就會慢慢失去學習興趣，只是機械地完成課后練習. 所以，在布置數學課后練習之前，教師要對練習進行細致的設計，明確練習目的，要思考練習過程中學生可能會遇到的問題，以及怎樣去分析、解決這些問題，進而真正起到練習的作用.

實踐出真知

現實生活是不斷變化的，因此教師要注意練習的多樣性，要使練習適應社會的發展. 同時，練習的多樣性要緊密結合課程內容以及教學目的，繼而實現既定的教學預期. 除了傳統的基礎理論練習，教師還可以設計社會調查、實踐操作、興趣培養等諸多形式的課后練習，培養學生的學習興趣，提升學生的數學能力.

案例2 同學們，請大家準備一張邊長為40 cm的正方形紙片，在它的四個角上同時減去邊長為x cm的正方形，再把剩下的紙折成一個無蓋紙盒，那么紙盒的容積y cm3和小正方形邊長x cm之間存在什么樣的關系？

生：y=x（40-2x）2.

師：x的取值范圍是什么呢？

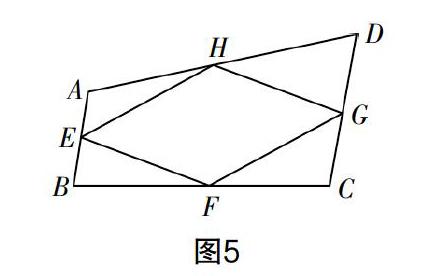
生：0

師：改變小正方形的邊長x，紙盒的容積y將會怎么變？在小正方形邊長x取何值時紙盒的容積最大？請同學們利用學過的數學知識進行探究.

評析 在初中數學的課程體系中，方法學習比單純的理論學習更具現實效用. 實踐教學是一種新的學習方式，是對傳統數學教學模式的改革與完善. 這種教學方式要求學生將數學學習融入生活實踐，用所學到的數學理論知識去解決生活中的問題，或者分析生活中出現的種種現象，使原本枯燥的理論知識具備活力. 在實踐的過程中，學生既能消化數學理論，又能增強數學應用能力與方法. 因此，設計課后練習時，既要保證一定的基礎理論訓練，又要豐富練習形式，布置一些實踐性、探究性均較強的練習.

減數量，保質量

在布置課后練習時，教師要根據課程內容和學生的學習情況合理安排練習的時間以及練習量，不要一味地依靠“題海戰術”，而應該為學生選擇典型的練習題，讓學生抓得住重點與難點，做到觸類旁通.

案例3 如圖5，E，F，G，H分別是四邊形ABCD四條邊的中點，順次連接E，F，G，H，則四邊形EFGH是什么四邊形？

生1：平行四邊形.

師：怎么證明？

生1：連接BD，構造△ABD與△CBD，由已知條件可知，EH為△ABD的中位線，FG為△CBD的中位線，所以EH=FG=BD. 同理，連接AC，則HG=EF=AC. 所以四邊形EFGH是平行四邊形.

師：生1的證明方法與結論都是正確的. 其他同學還有其他的證明方法嗎？

生2：可以證明一組對邊平行且相等，比如EH∥FG且EH=FG，或者EF∥HG且EF=HG，證明過程用到的也是三角形的中位線定理.

師：兩位同學的證明方法都正確. 同學們思考一下，如果這道題中的四邊形ABCD為平行四邊形、矩形、菱形、正方形時，結論又會是什么呢？

生3：仍然是平行四邊形，只不過會出現特殊情況. 如果四邊形ABCD為平行四邊形，那么四邊形EFGH為平行四邊形；如果四邊形ABCD為矩形，那么四邊形EFGH為菱形；如果四邊形ABCD為菱形，那么EFGH為矩形；如果四邊形ABCD為正方形，那么四邊形EFGH為正方形.

評析 像這樣的練習題，教師可以引導學生進行探索與討論，對原題可進行一定的修改與延伸，這樣能不斷地拓展學生的思維，增強數學學習的趣味性，引導學生將所學知識融會貫通，既提高學習效率，又提升學習效果.

層次要分明

學生個體間存在較大的差異，不同的學生在能力水平、學習習慣、學習成績等方面存在不小的差異. 在這樣的背景下，用相同的標準來要求所有的學生顯然不合適. 正因如此，教師在設計練習時要保證練習的層次性，設計不同的層次與難度梯度，供不同學習狀況的學生選擇，盡可能滿足所有學生的需求. 比如，對于學習存在較大困難的同學，教師可以布置教材上的基礎性練習，幫助這部分學生鞏固知識；對于學習尚可的學生，教師可以適量布置一些探究性練習，進一步激發這部分學生的學習能力；對于學習能力較強的學生，教師可以設計一些綜合性練習.

案例4 因式分解：（1）x2-16；（2）x2-16y2；（3）x4-16y4.

師：請同學們按照各自的分組，選擇一題進行因式分解.

評析 在本案例中，教師設計的三道題層層深入，便于不同學習狀況的學生理解，能使每一個學生都較好地解決問題，繼而增強學習興趣與信心.

結合上述內容，筆者認為練習在初中數學學習過程中極其重要，是數學學習的重要組成部分. 合理、科學的數學練習能幫助學生更好地理解知識內容，能掌握一定的數學技能，能促進學生進一步發展. 因此，廣大一線教師要重視數學練習，要精心設計，要激發學生的學習興趣，提升數學教學的有效性.