培養直覺思維，學會“跟著感覺走”

曹彩華

[摘 要] 在數學學習過程中，教師強調的“感覺”實質上是一種直覺思維，而直覺思維一定程度上能反映學生的創造力. 現如今，社會的快速發展對我們的創新思維能力要求較高，因此教育工作者要通過教學活動培養學生的直覺思維，促進學生全面發展.

[關鍵詞] 初中教學；直覺思維；人教版

數學強調的是邏輯思維，要求學生對問題進行理性思考. 但是，在聽取了一節習題公開課過后，筆者發現，在解題過程中，學生既需要嚴謹的數學思維，又需要一定的直覺思維，即不經過嚴格的邏輯思維就能理解問題、給出問題答案的能力，這樣能極大地簡化選擇題、填空題的解答過程，同時能為證明題、計算題等題型提供思路. 下面筆者結合教學實例進行闡述.

巧用對稱性

在現實世界中，很多事物的美都體現在其本身的對稱性上. 數學是生活的抽象，數學中的菱形、圓、拋物線等都是高度對稱的圖形. 在解決數學問題的過程中，學生常常會遇到看似不規則的、不對稱的圖形，但通過分割、補全、折疊等方式能使圖形出現對稱的部分，便于尋找其中的幾何關系或數量關系，進而應用各種定理或性質解決問題. 下面進行舉例說明.

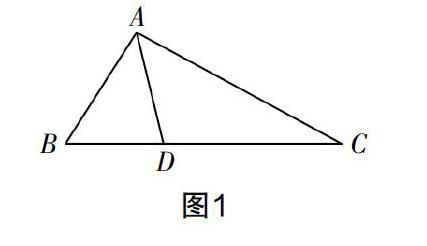
案例1 如圖1，在△ABC中，AD是∠BAC的平分線，且AC=AB+BD，試證明∠B=2∠C.

師：同學們，拿到這道題，大家認為哪一個條件是關鍵？

生1：AD是∠BAC的平分線.

師：既然題目中有一個角的平分線是已知條件，那大家會怎么使用呢？

生2：可以構造全等三角形.

師：具體怎么做呢？

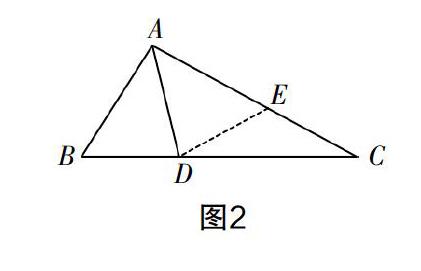
生3：以AD為對稱軸折疊三角形ABC，因為∠BAD與∠DAC相等，所以邊AB在折疊后會落在邊AC上，我們假設折疊后的點B落在點E處（如圖2），依據折疊的性質可得△BAD≌△EAD. 再結合“AC=AB+BD”這一條件可以證明∠B=∠C+∠EDC=2∠C.

評析 在這道題的證明過程中，學生利用角的軸對稱性進行直觀體會. 當然，在解題過程中，學生要適當繪制輔助線，便于思考. 圖形的對稱雖然不是一個直接考點，但在很多幾何題型中都會用到，具有較強的實用性，因此教師要引導學生深入感受這一思想方法，做到靈活運用.

學會數形結合

代數問題具有較強的抽象性，學生思考起來比較困難. 在處理一些代數問題時，學生可以借鑒幾何圖形，利用幾何圖形的性質來描述其中的數量關系，使思維過程更直觀，這樣的思維方法更符合中學生的認知.

案例2 已知正數m，n滿足m+n=2，試求+的最小值.

師：這道題是求最小值，最值問題的常規思路有哪些？

生1：函數.

師：那同學們覺得這道題構造成關于m或關于n的函數之后，該怎么求最小值呢？

生2：這個函數好復雜啊.

師：同學們再觀察一下“+”這個條件，什么樣的情況下會出現這樣的根式？

生3：想不起來了.

師：我再提醒一下，“”可以看成“”，“”可以看成“.

生4：直角三角形求斜邊長度！

師：很好！那這道題我們不從代數的角度去思考，我們借助直角三角形，將這道題轉化為兩個直角三角形斜邊之和. 那大家覺得該怎樣設置這兩個三角形呢？

生5：可以在長度為2的線段上設置動點，分別表示m與n.

師：來，把你構想的圖形畫到黑板上.

（生5于是在黑板上畫出了圖3，即AE=EF=2，BF=1，∠AEF=∠BFE=90°）

師：很好，這道題基本可以解決了. 哪位同學來說說答案是多少？

生6：根據“兩點之間，線段最短”，即A，C，B三點共線時值最小，可得最小值為.

評析在利用數形結合方法解決代數問題時，關鍵是明確幾何化的方法以及繪制怎樣的幾何圖形. 因此，這種方法的難點就是學生要對幾何問題以及代數問題有深刻的認識，能快速反應，將兩者進行聯系與轉化. 在學習與使用這種直觀方法的過程中，學生會漸漸明白同一個知識內容會有不同的表現形式，知識內容的學習不能固化，更不能僵化，要做到靈活變通，追本溯源，掌握核心.

類比思想

在解決實際數學問題的過程中，類比是一種直覺思維應用形式，這種思想方法需要尋找兩個對象的相似點，以此為基礎進行處理. 在解決問題時，學生如果能通過一個數學對象發現與之相類似的另一個對象，就能使用類比推理的方法進行解決.

案例3 已知線段AB上一共存在n個點（含端點A，B），那么這條線段上共有多少條線段？

師：在解決這個問題前，同學們先思考一下線段是由什么決定的.

生1：兩個端點.

師：兩個端點分前后順序嗎？

生2：線段與端點的前后順序無關.

師：沒錯. 明確了這兩點之后，我們先試著從一個端點出發. 哪位同學回答一下線段AB上任意一點構成的線段有多少條？

生3：（n-1）條.

師：那么所有的點構成了多少條線段？

生3：n×（n-1）條.

師：其他同學有不同的意見嗎？

生4：這樣算的話，每兩個端點因為前后順序不一樣而被計算了兩次，所以答案應該是條.

師：很好. 那接下來對這道題進行改編——如果從一個定點引出n條射線，一共能組成多少個角（不包含大于180°的角）？

生5：跟線段一樣，角只與兩條邊有關，且無序，所以一共可以組成個角.

評析 類比終究只是基于相似性的處理方法，所得到的結論不一定是正確的，并且結論還需要進一步驗證才能成立. 盡管如此，這種處理方法對于提升學生的直覺思維以及創造力來說具有較大的意義. 因此，在實際的教學活動環節，教師需要運用這種方法講授新知識，加強新、舊知識點之間的聯系，經常啟發學生，不斷提升學生的直覺思維能力.

合理猜想

案例4 如圖4，在等邊三角形ABC中，點E在AC上，且AE=CD，BQ⊥AD于點Q，BE交AD于點P，則BP-2PQ的值為（ ）

A. 1B. -1C. 0D. 無法確定

師：同學們，在做選擇題和填空題時，因為不需要書寫過程，因此大家可以根據已知信息大膽假設，根據假設找條件，去驗證自己的假設是否正確，這樣能給大家節省不少時間. 這是一種有效的應試技巧. 在這道題中，有“BQ⊥AD”這一條件，要求解的是一個二倍關系，同時選項中有“0”這樣一個特殊值，大家會進行怎樣的假設？

生1：∠PBQ=30°，BP=2PQ.

師：順著解題思路確實很容易有這樣的假設，看圖也比較符合，那如果這是一道證明題，嚴格證明的思路是什么呢？

生2：根據“SAS”可以證明△ABE≌△CAD，于是有∠ABE=∠CAD. 而△ABC是等邊三角形，所以∠BAC=60°. 所以∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°. 又BQ⊥AD，所以∠PBQ=30°. 所以BP=2PQ，即BP-2PQ=0.

評析 解決數學問題時，適時地進行猜想與假設也是一種有效的直覺思維，能簡化學生的思維過程，提升學生的創造力. 因此，在日常的課堂教學以及練習中，教師要選擇適當的練習題，引導學生進行猜想與假設，進而提高學生的直覺思維能力. 比如，在選擇題的解答過程中，可以“由果索因”，以已知選項為突破口，合理地進行假設，省略思維與解題過程.

綜上所述，在初中數學的學習過程中，提升學生的直覺思維能力也是教學重點，是課程改革的一大關鍵. 因此，廣大教師需要轉變固有的教學觀念，既要講授好知識內容，又要加強學生的直覺思維，引導學生大膽聯想，勇于質疑，科學驗證，繼而培養與提升學生的直覺思維能力.