注重“過程”的教學(xué)實(shí)例與思考

范文華

[摘 要] 對(duì)于初中數(shù)學(xué)，我們的教學(xué)不能僅僅盯著知識(shí)這一結(jié)果，還應(yīng)引導(dǎo)學(xué)生發(fā)現(xiàn)知識(shí)的形成過程，創(chuàng)設(shè)具體的情境，引導(dǎo)學(xué)生應(yīng)用知識(shí)解決實(shí)際問題，在教學(xué)中滲透數(shù)學(xué)思想方法，培養(yǎng)學(xué)生的數(shù)學(xué)素養(yǎng). 本文結(jié)合反比例函數(shù)圖像的研究，對(duì)過程教育的實(shí)踐課堂進(jìn)行思考與點(diǎn)評(píng).

[關(guān)鍵詞] 初中數(shù)學(xué)；過程教育

“過程教育”能培養(yǎng)學(xué)生的智慧，在過程中關(guān)注結(jié)果的形成、應(yīng)用以及數(shù)學(xué)思想方法，是新課程標(biāo)準(zhǔn)極力倡導(dǎo)的，但大多數(shù)教師在平日的課堂教學(xué)中卻對(duì)過程教育不是特別關(guān)注. 能夠直接解釋變量關(guān)系的反比例函數(shù)圖像在反比例函數(shù)的知識(shí)學(xué)習(xí)中相當(dāng)重要，本文是筆者基于反比例函數(shù)圖像的實(shí)際教學(xué)案例對(duì)過程教育所做的思考.

教學(xué)過程簡(jiǎn)錄

1. 環(huán)節(jié)1：課題揭示

第一步，教師在問題提出之前，明確指出反比例函數(shù)的研究內(nèi)容和方法與一次函數(shù)相似，將兩者進(jìn)行類比具有可操作性.

第二步，教師提出課前設(shè)計(jì)好的問題，并要求學(xué)生合作回答.

問題1：我們?cè)谘芯恳淮魏瘮?shù)時(shí)探究了哪些內(nèi)容？

問題2：你們還記得研究一次函數(shù)的過程嗎？

教師在學(xué)生的合作回答之后做出總結(jié)：

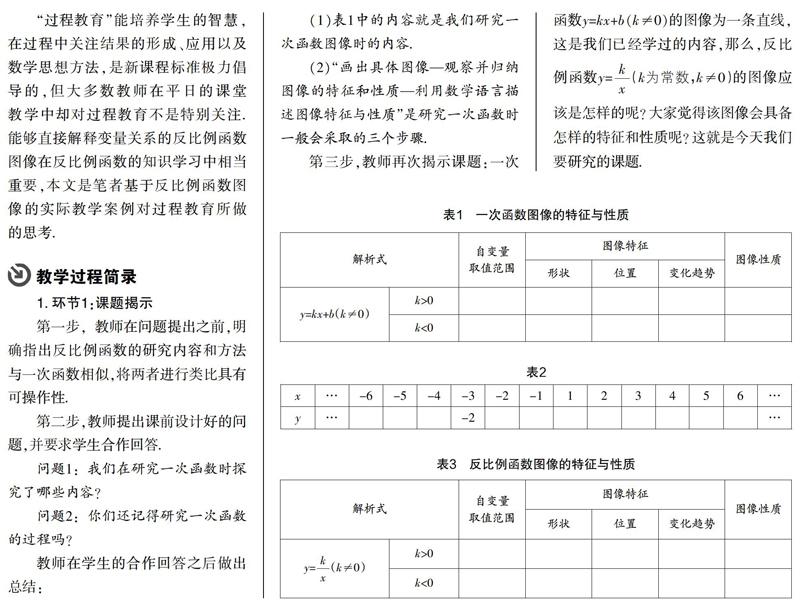
（1）表1中的內(nèi)容就是我們研究一次函數(shù)圖像時(shí)的內(nèi)容.

（2）“畫出具體圖像—觀察并歸納圖像的特征和性質(zhì)—利用數(shù)學(xué)語言描述圖像特征與性質(zhì)”是研究一次函數(shù)時(shí)一般會(huì)采取的三個(gè)步驟.

2. 環(huán)節(jié)2：反比例函數(shù)圖像的繪制活動(dòng)

步驟1：列表. 根據(jù)表2中x的值，求出對(duì)應(yīng)的y的值，并填入表2.

步驟2：描點(diǎn). 在直角坐標(biāo)系中一一描出表2中坐標(biāo)為（x，y）的點(diǎn).

步驟3：連接. 用曲線在第一、三象限內(nèi)按照自變量由小到大的順序?qū)⒏鼽c(diǎn)連接起來.

第二步，引導(dǎo)學(xué)生反思下列問題.

問題1：這一反比例函數(shù)圖像的制作過程經(jīng)歷了哪些步驟？

問題2：大家能否從表2中x的取值方法上獲得一定的經(jīng)驗(yàn)？

問題3：如果用線段來連接相鄰的兩個(gè)點(diǎn)，可以嗎？為什么？

問題4：應(yīng)該如何運(yùn)用函數(shù)解析式來解釋這一反比例函數(shù)圖像的趨勢(shì)及特征？

問題5：如果在該圖像上任意取點(diǎn)，并分別作出它們關(guān)于原點(diǎn)對(duì)稱的點(diǎn)，你有何發(fā)現(xiàn)？

教師在學(xué)生的合作探究之后進(jìn)行了總結(jié)：

（1）反比例函數(shù)的圖像一般會(huì)通過列表、描點(diǎn)以及連接這三個(gè)步驟繪制得到.

（2）x的值具有對(duì)稱性，且應(yīng)有利于y值的計(jì)算與描點(diǎn)；同時(shí)，x值的數(shù)量應(yīng)能使散點(diǎn)圖將函數(shù)圖像的整體輪廓反映出來.

（3）用線段來連接相鄰兩點(diǎn)的行為不可取，在相鄰兩點(diǎn)之間取幾個(gè)點(diǎn)進(jìn)行驗(yàn)證就能夠知曉.

（4）觀察這個(gè)函數(shù)解析式可以發(fā)現(xiàn)，自變量x是不能取0的，因此，反比例函數(shù)的圖像會(huì)越來越靠近x軸與y軸，卻始終不會(huì)與兩軸相交.

（5）在圖像上取任意一點(diǎn)，并求其關(guān)于原點(diǎn)對(duì)稱的點(diǎn)可以發(fā)現(xiàn)，它們都在該函數(shù)圖像上，這是點(diǎn)的坐標(biāo)滿足函數(shù)解析式的緣故.

（1）k為正數(shù)還是負(fù)數(shù)？

（2）你能寫出該反比例函數(shù)的表達(dá)式嗎？

（3）這個(gè)反比例函數(shù)圖像的另外一支應(yīng)該是怎樣的？請(qǐng)嘗試作圖.

第二步，要求學(xué)生合作回答.

第三步，教師追問：

（1）判斷的依據(jù)有哪些？具體過程中包含了哪些數(shù)學(xué)思想？

（2）你覺得該反比例函數(shù)的表達(dá)式中蘊(yùn)含了哪些數(shù)學(xué)思想？

（3）你是依據(jù)什么來繪制出該反比例函數(shù)圖像的另一支的？

教師隨即根據(jù)學(xué)生的合作回答情況做出一定的評(píng)價(jià)與總結(jié)，并要求學(xué)生獨(dú)立完成練習(xí).

5. 環(huán)節(jié)5：回顧與思考

第一步，列出設(shè)計(jì)好的問題清單，并引導(dǎo)學(xué)生對(duì)下列問題進(jìn)行回顧與思考.

（1）本課研究的內(nèi)容有哪些？是如何進(jìn)行研究的？

（2）請(qǐng)根據(jù)本課研究所獲得的感受與體會(huì)，對(duì)反比例函數(shù)圖像的特征和性質(zhì)進(jìn)行小結(jié)，并表達(dá)出來.

（3）反比例函數(shù)與一次函數(shù)相比，在圖像上存在哪些差異？

（4）請(qǐng)描述出反比例函數(shù)圖像的特征與性質(zhì)生成的基本過程.

（5）你覺得對(duì)于反比例函數(shù)，還有其他可研究的內(nèi)容嗎？

第二步，組織學(xué)生合作交流，并及時(shí)進(jìn)行評(píng)價(jià).

第三步，與學(xué)生一起就本課的研究內(nèi)容與方法進(jìn)行小結(jié).

（1）研究內(nèi)容：自變量的取值范圍、圖像特征、圖像性質(zhì).

（2）研究方法：數(shù)形結(jié)合、歸納、轉(zhuǎn)化等思想.

注重“過程”的教學(xué)思考

課堂教學(xué)的有效實(shí)施，應(yīng)該將認(rèn)知過程的“前半段”與“后半段”全都囊括其中. 數(shù)學(xué)結(jié)果應(yīng)該在認(rèn)知過程的前半段獲得，而其應(yīng)用則應(yīng)該在認(rèn)知過程的后半段進(jìn)行. 認(rèn)知的前半段屬于從感性到理性發(fā)展，并獲得結(jié)果的過程，認(rèn)知的后半段則是理性認(rèn)知逐步加深并能夠在實(shí)際問題中進(jìn)行解題與應(yīng)用. 本課的教學(xué)過程很好地囊括了這兩個(gè)過程，這完全符合新課程所提倡的過程教育理念與要求，其在操作上一般具有下列特征.

（1）教學(xué)內(nèi)容應(yīng)依據(jù)過程教育而確定.

數(shù)學(xué)的結(jié)果、結(jié)果的形成，以及應(yīng)用和過程中所蘊(yùn)含的數(shù)學(xué)思想方法，都是過程教育中的重要內(nèi)容. 本課教學(xué)中所包含的反比例函數(shù)圖像的產(chǎn)生、演繹、數(shù)形結(jié)合思想、圖像特征與性質(zhì)等，都能很好地體現(xiàn)這一點(diǎn).

（2）教學(xué)結(jié)構(gòu)應(yīng)依據(jù)過程教育而建構(gòu).

過程教育理念指引下的教學(xué)結(jié)構(gòu)符合數(shù)學(xué)的發(fā)展規(guī)律、學(xué)生的認(rèn)知規(guī)律，以及教育教學(xué)的規(guī)律，本課所體現(xiàn)的教學(xué)結(jié)構(gòu)與這一系列邏輯連貫的規(guī)律完全吻合，具體體現(xiàn)如圖2.

（3）操作方法應(yīng)依據(jù)過程教育而選擇.

基于過程教育的數(shù)學(xué)活動(dòng)，應(yīng)選擇能夠符合學(xué)生最近發(fā)展區(qū)與認(rèn)知規(guī)律的操作性活動(dòng)，準(zhǔn)確、清晰且富有啟發(fā)性講解的，以及學(xué)生所經(jīng)歷的實(shí)質(zhì)性思維過程，都能更好地促進(jìn)教學(xué)目標(biāo)的實(shí)現(xiàn).

本課中的每個(gè)教學(xué)環(huán)節(jié)都能體現(xiàn)這些觀點(diǎn)：

（1）課題的揭示過程符合過程教育理念. 教師采取教師引導(dǎo)、學(xué)生合作、教師總結(jié)等方式對(duì)具備定向指導(dǎo)性的問題進(jìn)行探索，使得認(rèn)知的全過程都包含在一次又一次的合作探究中，知識(shí)的探索與呈現(xiàn)過程符合過程教育以及導(dǎo)入性教學(xué)的基本主張.

（2）反比例函數(shù)圖像的繪制活動(dòng)符合過程教育的主張. 反比例函數(shù)圖像的生成是這一章節(jié)知識(shí)體系中最基本的研究條件. 學(xué)生在教師的引導(dǎo)下獨(dú)立學(xué)習(xí)、反思繪圖、變式訓(xùn)練，整個(gè)過程符合過程教育的理念，以及以學(xué)為中心的思想.

（3）反比例函數(shù)圖像特征與性質(zhì)的探索活動(dòng)符合過程教育的理念. 這一探索活動(dòng)中隱含著培養(yǎng)學(xué)生能力發(fā)展、個(gè)性養(yǎng)成以及創(chuàng)新精神培養(yǎng)的重要基點(diǎn)，這一實(shí)質(zhì)性思維過程符合過程教育的理念，以及以學(xué)為中心的思想.

（4）嘗試應(yīng)用的活動(dòng)符合過程教育理念. 運(yùn)用數(shù)學(xué)結(jié)果來進(jìn)行具體問題的解決屬于認(rèn)知過程的后半段，本課借助課本習(xí)題令學(xué)生在問題引導(dǎo)、合作解答、教師追問中獲得知識(shí)運(yùn)用的方法，同樣符合過程教育理念.

（5）回顧與思考活動(dòng)符合過程教育理念. 在研究內(nèi)容與方法上獲得進(jìn)一步的感受，屬于認(rèn)知過程的后半段，其對(duì)于深化認(rèn)識(shí)、增強(qiáng)學(xué)生的反思意識(shí)、培養(yǎng)學(xué)生的表達(dá)能力等都有著巨大的意義.

本課的教學(xué)策略符合認(rèn)知過程中前、后過程的過程教育理念，教師所引導(dǎo)和實(shí)施的先“放”后“收”教學(xué)方法具備普遍的適用性，且與過程教育的精神實(shí)質(zhì)完全吻合.