基于三大策略 滲透數學思想

李瓊珍

[摘要]在小學數學課堂教學實踐中，教師應善于發掘數學知識的思想層面，在日常教學中滲透數學思想。一方面要創設情境展開深入發掘，突出數學思想的重要性;另一方面，在新知的學習階段，要加大對學習過程特別是數學思想的關注;除此之外，還要在延伸階段不斷深化學生對數學思想的認知與運用。具體而言，要深挖教材，在情境中滲透數學思想;關注過程，在學習中滲透數學思想;強調運用，在練習中滲透數學思想。

[關鍵詞]小學數學;數學思想;滲透

伴隨著新課程改革的不斷深入，數學教學逐漸加大了對三維目標的關注。根據《數學課程標準》（2011版）中的相關規定，基本數學思想已經成為教學中不可忽視的重要基礎目標。在當前的小學數學教學中，教師只重視數學基礎知識和技能的傳授是遠遠不夠的，還要引導學生掌握數學思想方法。這就要求教師在日常教學中要善于發掘數學知識的思想層面，積極滲透數學思想，培養小學生數學綜合能力。

一、深挖教材——在情境中滲透數學思想

當前，在小學數學教學實踐中，情境圖的應用越來越廣泛。以北師大版小學數學教材為例，其典型特征就是基于“情境圖+問題串”的方式向學生展示數學信息。教師應注意的是，情境的創設絕不可毫無目的，應當結合教材內容深入發掘，由此才能夠充分凸顯蘊含在情景圖中的數學思想。

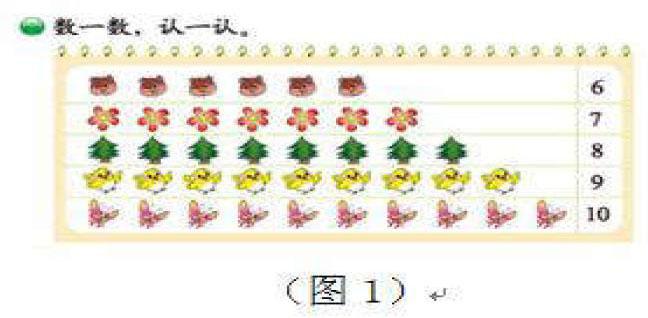
例如，在一年級上冊教材中設置了如下情境圖（圖1），目的就是為了使學生通過對情境圖的認知，感受物體所對應的個數，由此形成“6～10”的概念。

在情景圖中所展現的物體都是小學生能夠在生活中經常見到的，實際上這也滲透了很多數學思想：1.集合的思想。與一個數字相對應的是一類物體，這類物體就能夠形成一個集合。2.一一對應的數學思想。在情境圖中，每一種物體的集合都與一個自然數相對應，為學生提供了數數的載體。在教學實踐中，教師應當給予學生正確的引導，讓學生在數數的過程中感受集合思想和一一對應思想，全面系統地提升學生的數學素養。

二、關注過程——在學習中滲透數學思想

在小學數學教學實踐中，教師應善于滲透數學思想，讓學生在習得相應知識的同時，體會到數學思想的獨特魅力。

1.在新知學習中滲透數學思想

《數學課程標準》特別強調，數學教學應結合學生的生活經驗，將實際問題抽象演變成為數學模型，使學生可以親歷完成解釋和應用的這一過程。小學生對數學知識的學習過程，實際上正是對數學模型的理解與把握的過程。在這一過程中，教師應善于引導學生從中體會數學思想，提升教學實效。

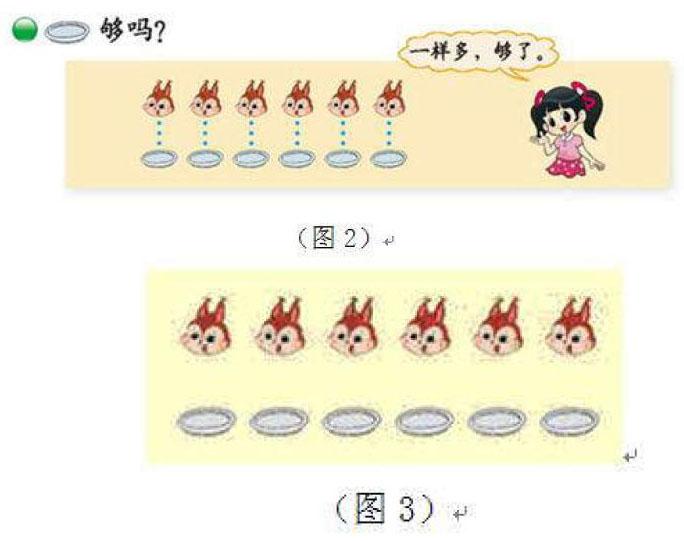
例如，一年級上冊教材第14頁中所呈現的情境圖是“小松鼠分盤子”（圖2），這幅圖意在引導學生感受數學概念“一樣多”。

關于物體個數的比較，學生在幼兒園的時候就已經有所接觸，但是，他們的理解往往相對淺顯，通常是基于對數量的比較或者基于自己的感覺。在實際教學實踐中，教師應通過如下方式幫助學生樹立正確的“同樣多”的概念（圖3）。

師：同學們，如果每一個小松鼠吃飯都需要用一個盤子，那么，上面的小松鼠都能夠分到各自的盤子嗎？

生1：剛好每個松鼠都對應一個盤子。

生2：每只松鼠的下面都有一個，也就是夠分。

師：大家回答得都很好。那么，如果讓你們借助畫圖的方法，怎樣才能夠說明每個松鼠都能分得一個盤子呢？

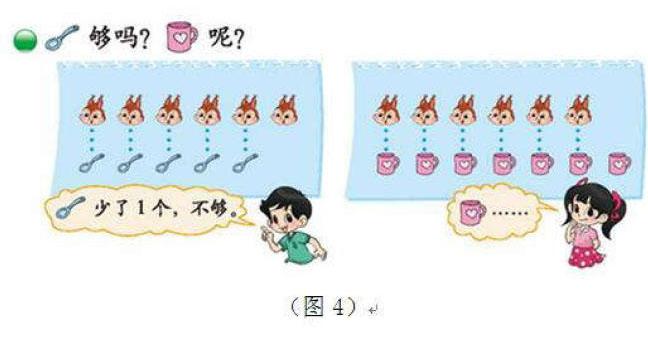
接下來就是學生的動手操作環節。根據學生所展示的學習成果，教師向學生展示圖2。基于小兔和磚塊的一一對應關系，學生了解到通過這一方式可以快速有效地對兩種物體進行數量比較。之后，教師向學生再一次展示情景圖（圖4）：

教師向學生布置畫圖任務，通過畫圖解決問題：是否每一個小松鼠都能夠分得一個勺子和一個杯子？

借助這樣的情景，學生在分盤子、勺子以及杯子的過程中，能夠利用畫圖的方式掌握比較大小的方法，還可以充分領悟一一對應的數學思想。

2.在數學探究中滲透數學思想

在課堂教學中，教師應正確引導學生，使學生可以在自主探究的過程中習得數學知識、感悟數學思想。

例如，第八冊教材中《梯形的面積》一課，其教學重點在于引導學生自主推導出梯形的面積公式。在具體教學實踐中，教師普遍采用對接的方式，將兩個完全相同的平行四邊形合成一個梯形，這樣學生可以根據已經掌握的平行四邊形面積公式自主推導出梯形面積公式。但是，在這一過程中，學生不能充分感悟轉化的數學思想，主要是因為圖形的轉化源自于教師。所以，教師應當將教學重點放置于“如何求梯形的面積”這一問題上，先引導學生進行充分思考：如何才能根據已經學習過的面積公式，實現對梯形面積公式的推導？之后再引導學生進行動手操作實踐，自主發現通過兩個完全相同的平行四邊形的對接可以獲得一個梯形。這樣的公式推導過程才能夠水到渠成，學生才能夠印象深刻。當學生充分理解并掌握轉化思想之后，教師可以向學生出示題目：1+2+3+4+……+10=？實際上，解決這道題是對初中階段“連續正整數的求和”相關內容的預教學，既有助于學生運用轉化思想，也有助于實現相關知識的滲透。

三、強調運用——在練習中滲透數學思想

1.在運用中滲透數學思想

當學生通過自主學習完成對數學知識的建模之后，引導學生如何利用所學的知識則是教學的關鍵。在這一過程中，教師應結合教材范例中所蘊含的數學思想進行有效的教學延伸。

例如，二年級上冊教材第97頁有如下習題（圖5），在實際教學過程中，教學重點不僅是完成填空，還需要有效滲透函數的基本思想。在習題2中，不管是先減7再加14，還是先除以3再乘以5，隨著被加數和被除數的改變，其結果也會呈現不同的變化，這有助于學生感受數的變化，掌握“即使運算過程沒有發生改變，結果仍然變化”這一思想。

2.在解題中滲透數學思想

問題是引導學生展開數學學習的有效載體，解決問題可以幫助學生準確把握相應的知識。為了有效降低問題的難度，可以借助轉化的思想。

例如，在數學問題中，最典型的莫過于“雞兔同籠”。在小學階段，這一題目的出現是為了引導學生展開數學猜想，并通過驗證有效解決問題，在猜想與驗證的過程中正是采用了轉化的思想。教師可以借助列表的方法，讓學生充分領悟轉化法的精妙之處，這樣既有助于學生掌握相應的數學知識，也能夠實現轉化思想的有效滲透。

總之，在日常教學中，教師應有意識、有計劃地滲透數學思想方法，讓學生不但能夠掌握相應的數學知識，還能夠有效借助數學方法提升自主學習能力。

參考文獻：

[1]馬生宏.論如何在小學數學教學中滲透數學思想方法[J].吉林教育，2014，（02）.

[2]魏尚忠.淺談數學思想在小學數學教學中的滲透[J].吉林教育，2014，（02）.

[3]楊麗.讓數學思想方法在學生腦海里“扎根”[J].教育教學論壇，2014，（07）.

注：本文系泉州市教育科學“十三五”規劃（第一批）課題“小學數學思想方法教學的研究”（立項編號：QG1351-102）的研究成果。

（責任編輯 趙永玲）