用好教材 追求真實的教學

楊世玉

摘要：情境教學一直是我們非常關注的問題，教材情境更是被津津樂道，教材為我們提供了豐富多彩的情境資源，如何讓教材情境為我所用，是值得我們每一位教師深思的，本文擬從教材情境資源的使用、整合、更換三個維度進行研究。

關鍵詞：情境資源;使用;整合;更換

何謂情境？“情境是利用一個熟悉的參照物，幫助學習者將一個要探究的概念與熟悉的經驗聯系起來，引導他們利用這些經驗來解釋、說明，形成自己的科學知識。”教材提供的情境一般都是適宜兒童的情境，但教材它具有普適性，它提供的情境并不一定適合每一個區域的孩子，這就需要教師自己去識別、辨取。本文拙借三個片段談談自己對教材情境資源利用的粗淺認識。

一、何須舍近求遠——教材情境之“使用”篇

【案例】

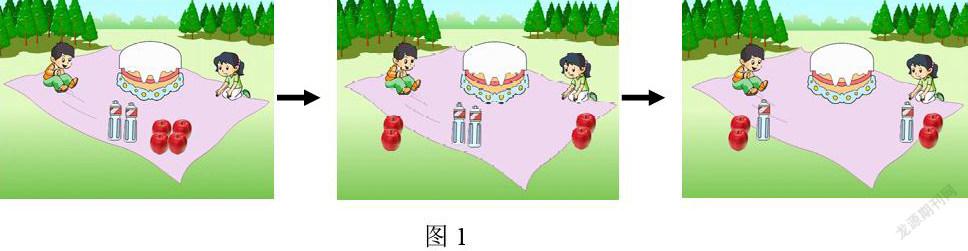
蘇教版《分數的初步認識》，教材提供的教學情境如下：

師：4個蘋果平均分給兩個小朋友，每人分得幾個？

生：每人分得2個。

師：2瓶礦泉水平均分給兩個小朋友，每人分得幾瓶？

生：每人分得1瓶。

師：蛋糕只有一個，怎么分呢？

生：每人分半個。

師：真是好主意，那這一半怎樣用數來表示呢？

【思考】

《分數的初步認識》可以說是一節經典課，很多老師執教過這一課，分餅、分西瓜、分桃子、甚至分漢堡包、披薩餅……，有的老師認為反正一定要跟別人分的不一樣才行，才能顯示出情境創設的不一般。

我們再選取幾個版本的教材來看一看，蘇教版教材創設的情境是先把4個蘋果平均分，再把2瓶礦泉水平均分，最后把1個蛋糕進行平均分;人教版教材創設的情境是把一個月餅平均分;北師大版教材創設的情境是把一個蘋果平均分。其實這幾個版本教材創設的情境都不錯，何必再煞費苦心的找別的東西來分，甚至于有的改編根本就不適于平均分。

如果從嚴密性來說，我認為人教版將一個月餅平均分，用二分之一來表示半塊月餅更為合理。北師大版將一個蘋果進行平均分，蘋果要平均分成完全相同的兩份，其實還真挺困難，生活中大多數的蘋果都不是兩邊完全對稱的，再說，生活中誰切蘋果連柄都切兩半。蘇教版是將蛋糕進行平均分，倒是可以分成完全相同的兩半，只是教材中提供的蛋糕圖不是完全規則的形狀。

如果從過程性來看，我會更傾向于蘇教版的編排，從把4個蘋果進行平均分，到把2瓶礦泉水進行平均分，很自然地過渡到把1個蛋糕進行平均分，不漏痕跡地把學生輕松引入分數的世界。從每人分得2個到每人分得1個再到每人分得半個，這是一個漸進的過程，是一個從整數過渡到分數的過程，符合孩子的認知規律。與此同時，這樣的情境也激發了學生的認知需求，這半個怎樣用數來表示，孩子們會非常好奇，自然會有學習新知的欲望。

二、未必盡善盡美——教材情境之“更換” 篇

【案例】

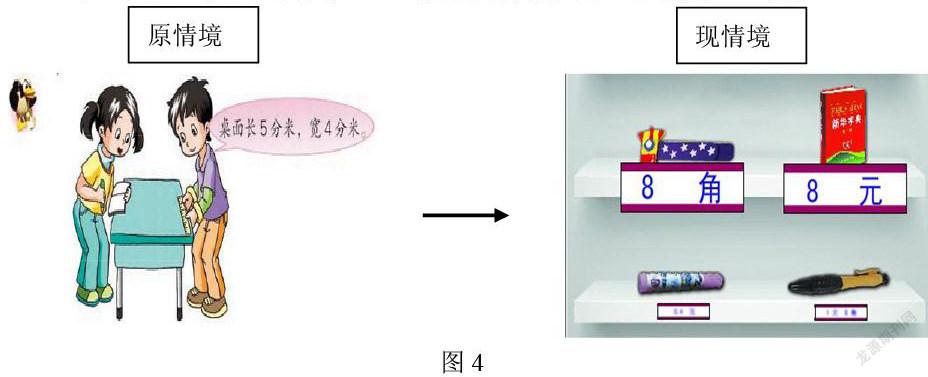
《認識一位小數》中教材提供的情境是通過測量課桌長寬引出小數，我們在教授這一課時，將測量情境更換為購物情境。

師：孩子們，再過幾天，就要迎來我們自己的節日，你們知道是什么節日嗎？

生：六一兒童節。（欣喜地）

師：小明的媽媽準備買一些禮物送給小明，瞧！她來到了商店的貨架前，準備買一張書簽（8角）和一本字典（8元），它們的價格相同嗎？

生：不同。

師：哪里不同？?生：單位不同。

師：什么相同？?生：前面都是數字8。

師：8是一個自然數，我們以前學過的表示物體個數的1、2、3……都是自然數，0也是自然數，它們都是整數。

師：這兩個價格的單位不同，誰會用相同的單位來表示呢？

生：8角也可以看成0.8元。

師：像0.8這樣的數，你知道它叫什么數嗎？

生：小數。

師：今天就讓我們一起來認識小數，關于小數，你想了解哪些知識呢？

【思考】

教材所提供的情境，不可能每一個對于我們來說都適用，不適宜的，完全可以更換。比如《認識一位小數》，教材提供的教學情境是測量課桌面的長和寬，得出桌面長5分米是米，寬4分米是米，再告訴學生米還可以寫成0.5米，米還可以寫成0.4米。課前我認真分析了學生的認知起點，學生已認識米和分米，知道1米等于10分米，也能建立起5分米就是把1米平均分成10份表示其中的5份這樣的表象。通過得不到整米數的測量活動引出小數，這樣的情境確實能體現出認知的需求。可存在的問題是教學的時間非常有限，測量活動必然要用去大量的時間，還并不一定能得到這節課需要的數據，在并非本課的重點環節耗費不必要的大量時間，這樣的教學很難說的有效的教學。如果不設置測量環節，直接呈現信息：課桌面長5分米、寬4分米，學生很難產生強烈的認知需求，而且三年級學生對分米這樣的長度單位，在生活中的接觸并不是非常廣泛。如果將下面這兩種情況進行比較：5分米是把1米平均分成10份占其中的5份，5角是把1元平均分成10份占其中的5份，哪一種情況對于學生來說更容易形成表象呢，即哪一種更直觀、更形象呢？我認為元與角的關系更優于米和分米的關系。

那教材的教學情境是不是可以進行更換呢？為此，我進行了課前的前測，對沒有學習過小數的三年級學生進行了調查，調查分為以下幾項：1.是否見過像0.5這樣的數？在哪見過？2.會不會讀這個數？3.你知道這個數表示什么意思嗎？100%的孩子表示見過，多數孩子表示是在買東西時見過;90%的孩子會讀（只是口頭讀，并不是書寫0.5讀作零點五）;10%的孩子能解釋0.5表示的意思，有的孩子說0.5表示一半，有的孩子用元與角之間的進率來解釋，0.5元就是5角。基于這樣的前測，本節課從關注學生的認知起點出發，用元與角之間的進率來引入小數，以喚醒學生已有的數學現實，拓展學生已有的認知經驗，從而提高課堂教學的有效性。

教材提供的情境資源，用或是不用？如何用？用到什么程度？都是值得我們一線教師深思并探討的問題。

參考文獻：

[1]義務教育《數學課程標準》，北京師范大學出版社，2011年版。

[2][美]喬納森編，鄭太年等譯：《學習環境理論基礎》華東師范大學出版社，2002年版。