評一節課所感細節的重要性

嚴偉趙

摘要：聽課是教師繞不開的一項工作，之后科學的評課對改進教師的教學行為、提高教師的教學藝術和課堂教學質量，提升教師教育教學素養、促進教師的專業發展有著非常重要的作用。評課是教學、教研工作過程中一項非常有意義的活動，通過評課，同事之間可以相互學習，相互促進，把握好教學，為課堂教學的有效性指明方向。

關鍵詞：聽課;評課;有效教學

評課是一門藝術、一門學問，教師上好課是為了提高課堂教學質量，而學習如何評好課也同樣能激勵授課與評課教師根據聽課后的感悟材料來更好的備課與上課。所以說評好課也是為課堂教學有效性服務的。實際上，上好課與評好課不是獨立的個體，而是相互統一，相互促進的。學習如何評好一堂課，同樣有助于提高自身的教學。特別是專家老師提出的評課原則、評課內容讓我記憶猶新，使我受益匪淺，讓我覺得自己需要學習的地方還有很多。下面結合學習和平時的一些做法，對評課能促進課堂教學有效性講講自己的一點想法。

一、從“心”開始，積極認真評價一節課

在一次聽課活動中，一節《解直角三角形復習》的引入是這樣的：“同學們已經復習過三角形的知識，對三角形已有了更深入的了解。現在請同學們觀察這個直角三角形，從中你能獲得哪些信息？

問題1：若把的各邊都擴大2倍，得到，則嗎？

問題2：若把的∠變為原來的兩倍（0°﹤2∠﹤90°），得到，那么嗎？”

這節課我的感覺，復習課的定位：復習課要幫助學生領會考試的要求，樹立必勝的信心;復習課要讓學生明確本章節的重點和難點;復習課要重知識結構的梳理，重解題策略的形成，重數學思想方法的滲透。（現在老師對此重視嗎？）

復習課的任務：回顧過去所學的知識并形成良好的知識結構——梳理知識;

進一步鞏固、掌握《課程標準》規定的基礎知識、基本技能和基本方法——落實“三基”;

揭示規律，總結方法，形成策略，提高學生靈活應用知識解決問題的能力。

今天上課的老師選題用心，（1）應用問題靈活——提高學生能力;（2）主線清晰;（3）關注問題的分析;（4）對于數學思想方法的提煉和深究。

這節課第1個問題比較開放，由角到邊之比后下面的問題進行太快，邊擴大2倍、角擴大2倍會怎樣，過程慢一點，學生的情緒更高，可以問學生這些學了有什么用處呢（學生可能想到可以量旗桿的高度）。設計的不夠充分。可以放開給學生多留時間給學生會更好。

同時還要注意復習的策略：一、鞏固知識，以練為主;二、查漏補缺，調查為先;三、拓展提高，思維為重。在這些方面老師都已經關注到了。

二、從“情”入手，努力評好一節隨堂課

實話實說對于評課教師來講，是一種最基本的要求，同時也是一種很重要的責任心問題。要明確評價教師的基本功，還要評價課堂的結構、教學方法、學生學習的效果。比如，不久前我也在校內的一節組內公開課上的復習課《解直角三角形》，設計是這樣的：

回顧特殊角度的三角函數值，然后安排練習：

（1）計算：sin60°·tan60°+cos?45°=_________;

（2）如果tanA·tan30°=1，∠A=_________;

（3）已知<0.5，那么銳角α的取值范圍是_________

例題、海島A四周20海里周圍內為暗礁區，一艘貨輪由東向西航行，在B處見島A在北偏西60?方向，航行24海里到C處，見島A在北偏西30?方向，貨輪繼續向西航行，有無觸礁的危險？

提高題小島A在港口P的南偏西45°方向，距離港口81海里處。甲船從A出發，沿AP方向以9海里/小時的速度駛向港口，乙船從港口P出發，沿南偏東60°方向，以18海里/小時的速度駛離港口，現兩船同時出發。

（1）出發后幾小時兩船到港口P的距離相等？

（2）出發幾小時乙船在甲船的正東方向（結果精確到0.1h）”。

我感覺這節課的設計一般，所選的題目偏難，造成許多學生不能很好地掌握相關知識。沒有較好的梯度，一開始就較難。對解直角三角形的知識點的落實不夠，重點不夠突出。教師給予的思考時間和空間較多，學生的參與度較好。教師的講解還是偏多一點，對解法的指導不夠，應把問題轉化為解直角三角形，利用化歸思想，給出一種普遍性問題的解法。以致于后面就體現不出復習課該有的知識提升這一境界。

經過我們坦誠地交流，知道在哪些方面是需要提高的，以及知道自己的優點（如能充分讓學生思考就是優點）;但是數學思想的形成是一個逐步滲透的長期過程，必須以數學問題為載體，經過循序漸進和反復練習，才能使學生真正地有所領悟，這方面我這節課是有所欠缺的。常言道“當事者迷，旁觀者清”，上課教師在上課過程中所暴露出來的問題，如果沒有別人指出來，是很難自己發現自己的成功之處和不足之處的。因此，評課時如果聽課人員能把上課過程中所暴露出來的問題診斷出來，然后再誠懇地給提出來，這無疑是對上課教師的莫大幫助。

三、從“理”著眼，用心改好一節隨堂課

在后來的改進中上課老師改變原來的教學設計，其中引入這一環節是這樣處理的：

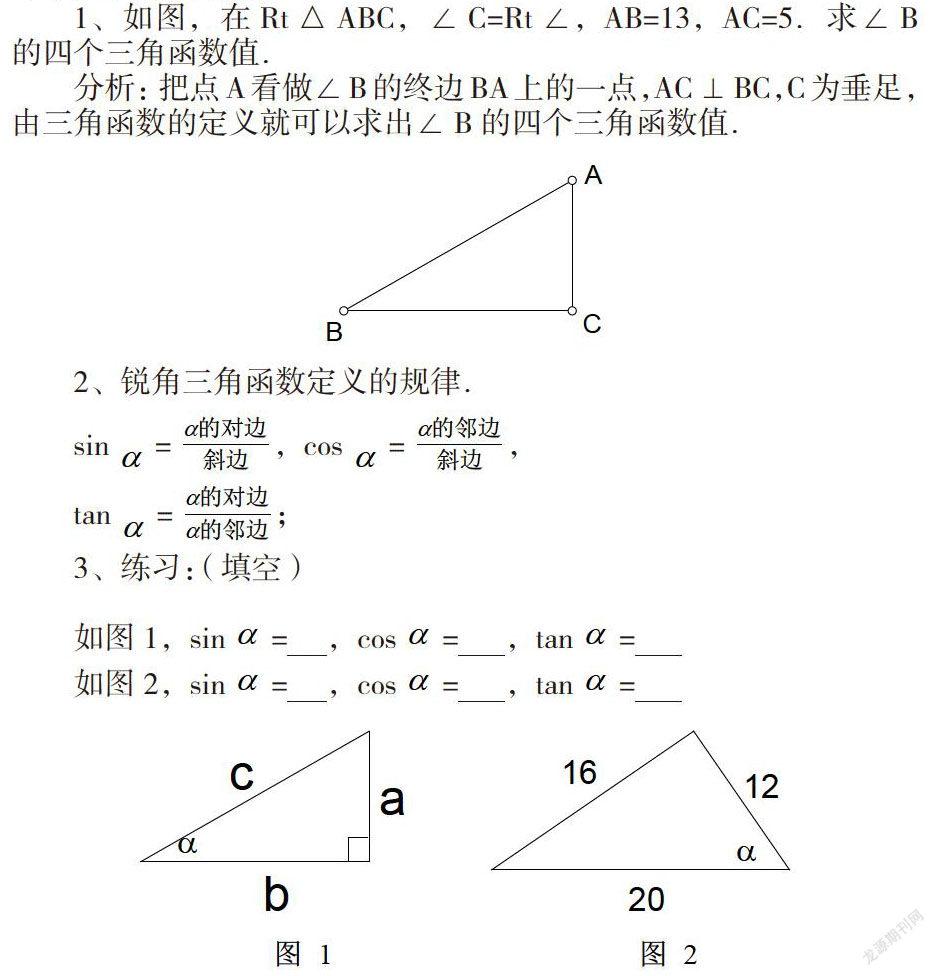
1、如圖，在Rt△ABC，∠C=Rt∠，AB=13，AC=5.求∠B的四個三角函數值.

分析：把點A看做∠B的終邊BA上的一點，AC⊥BC，C為垂足，由三角函數的定義就可以求出∠B的四個三角函數值.

2、銳角三角函數定義的規律.

sin=_________，cos=_________，tan=_________;

3、練習：（填空）

如圖1，sin=_________???? ，cos=_________????? ，tan=????_________

如圖2，sin=?_________??? ，cos=?_________???? ，tan=?????_________

4、已知Rt△ABC中，∠C=Rt∠，求證：cosA = sinB.

大題目的順序不變，只是把例題中的30°改為40°，突出解直角三角形的一般解題過程，找到一種有效的通解。雖然只是這么簡單的一改，但是其中的數學味就馬上呈現出來了，給學生思考的空間就明顯變大了。

經過這樣的修改之后，學生的課堂氣氛明顯要好于上次上的公開課，而且課堂教學的有效性也得到保證。由此可見，真心實意的評課對于課堂有效教學是有多么重要。

總之，在新形勢下，要想成為一名優秀的教師既需要學會如何上課，也需要學會如何評課，也只有這樣，久而久之我們才能成為業務素質精良、教學技能全面、教學基本功過硬、具有一定教科研能力、適應新時期新課程改革需求的教師。

參考文獻

[1]岑志慶新課程標準下初中數學課堂教學有效性策略研究考試周刊，2007

[2]鄭信軍張曉瑜現代教育理論與實踐2002

[3]方明一中小學數學教學的美育探微2010