基于博弈論和神經網絡算法最優路徑的設計
李曉啟 崔麗琪 宋昱開






摘要:本文主要研究了旅游景點的應急疏散方案問題。樓層平面內通過博弈論和元胞自動機原理建立了多口人群疏散模型,樓層間通過圖論和神經網絡算法建立了網絡路徑優化算法模型。結合這兩個模型為景點提供最佳的游客疏散方案。通過層次分析法,將游客疏散分為:在發生緊急情況時游客找到所在樓層的逃生通道和從逃生通道撤離到出口兩個過程。在緊急情況發生后,游客會自己選擇逃生通道,依據博弈論分析游客權衡出口的寬度和人數、游客距出口的距離,以及出口的阻塞程度等權重后做出選擇,當游客去一個通道的收益為最大時,這個出口將成為他首要選擇的目標。最終計算出在疏散時選擇在就近通道口排隊和選擇去其他的通道口人數的比例為2:8時,所用時間最短,并使用MATLAB軟件對模型進行了仿真分析,計算出使用模型人口疏散的時間比不使用模型一提速了4%,從而證明了模型的合理性。
關鍵詞:人員疏散 敏感性解析 層次分析法 博弈論
1問題重述(略)
2模型假設
1)假設每層的參觀者分布均勻;
2)疏散時,人員只向前移動,而不是后退或原地旋轉;
3)每層樓的所有入口都變成出口,電梯和自動扶梯停止運行(停止的自動扶梯可用作樓梯),樓梯可以正常使用。
3 模型的建立與求解
人員疏散時對出口的選擇過程類似于很多人對有限資源的搶占,人員之間是相互競爭的關系,每個人的目標都是盡快的通過出口。當出口阻塞時該在最近出口附近等待還是應立即更換較遠出口問題可通過建立如下模型解決[1]。
但此時模型為逃生者之間的不完全信息的靜態博弈,站在策略制定者的角度,利用元胞自動機模型,基于二維離散空間,劃分空間分隔為均勻的網格,網格可以由個體占據,也可以由障礙物等占據。每一個個體占據網格上特定的位置,根據更新規則從一個網格位置移動到另一個網格位置[4]。
模型時間上采用離散的時間設置,每一個個體向相鄰網格移動后按照指定的規則進行更新[5]。綜合考慮路徑規劃、碰撞檢測、沖突消解問題,同時參考A-gent模型個體特定屬性,反映復雜的人類行為,包括學習其他的逃生策略,疏散路線,適應初始環境所給定的限制等。從空間演化博弈角度,假設所有逃生者的決策是理智,利用元胞自動機的基本框架,智能體模型( Agent- Based Model)來模擬獨立存在的個體的行為和個體間的互動,即人群疏散過程中,個體在和其他人員發生沖突時,個體采取競爭策略還是合作策略,就是個體和鄰域中其他人員的一個囚徒困境博弈,從而描述逃生者的行為[6]。
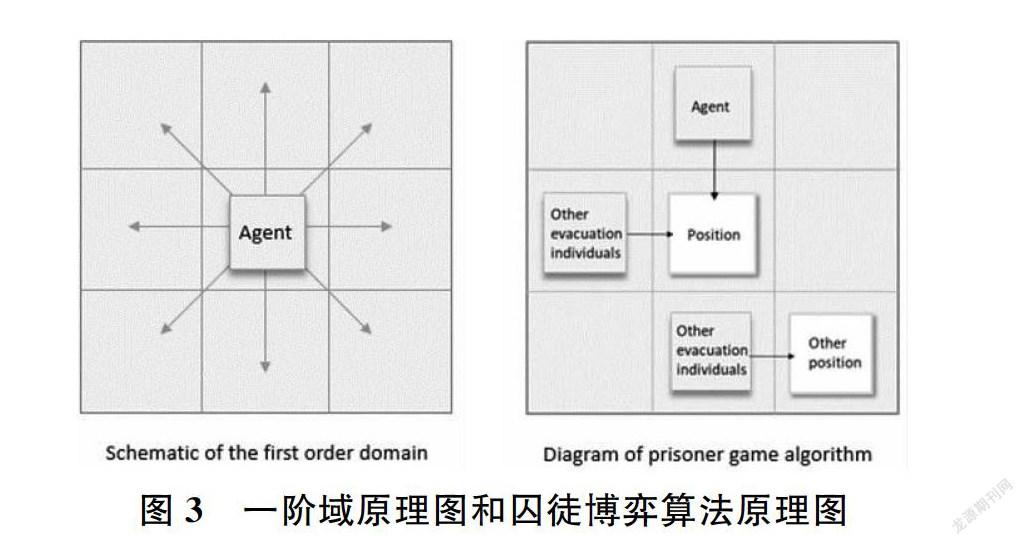
在此疏散模型中,位置的同步更新、異步更新、隨機更新的結果是一樣的。三種順序的更新都會考慮到周圍鄰域其他疏散個體博弈收益的影響,此影響是和更新順序無關的[7],示意圖如圖3。
參考Swarm仿真結果,模擬復雜的人類行為,提供對環境更加現實的自然描述,預測在出口處人流和疏散時間的關系,即已知靜態博弈中其他逃生者策略的情況下,規劃每個逃生者根據其他人員對出口的選擇時采用的策略,并通過應急人員或指示圖標布置實現策略,從而獲得最大收益,即以最短時間逃出平面空間,這恰好能很現實的反映緊急狀況下人員自身利益最大化的策略選擇行為。
最終計算出在疏散時選擇在就近通道口排隊和選擇去其他的通道口人數的比例為:2:8時所用時間最短。
4 模型的檢驗
為驗證模型的效果,采用MATLAB編程實現了一個多出口房間的疏散仿真,在15m×15m沒有任何設施的空房間中初始隨機分布100人,房間的4個出口如圖5所示分布(上下兩個出口寬度為0. 8m,右側兩個出口寬度為1. 2m)。按照指定參數進行疏散。即區域內選擇在就近通道口排隊和選擇去其他的通道口人數的比例為2:8。
由此可得出,使用基于博弈論和元胞自動機的多口人群疏散模型得出的出口安排,比最短路徑至少提速4%,如圖6所示。
5總結
依據建模結論,針對大型建筑應急疏散,以盧浮宮為例,對于特殊旅客方面:盧浮官2018年的參觀游客中,外國游客占比75%,因此盧浮官需要更多的具備這些外語交流能力的工作人員。若結伴旅行的游客(常常指旅行團),始終以團隊為單位行動,則可能會造成某撤離必經之路上的擁堵,這樣其他的通道不得不為此通道分壓,從而使整個疏散系統擁堵的可能性增加,甚至引起群眾恐慌,造成更加嚴重的后果。所以結伴旅行的游客,在疏散時應該遵循應急疏散方案,盡快撤離到安全地區。對于殘疾旅客:一般殘疾的游客會在家屬的陪同下參觀,發生緊急情況時,家屬會在幫助殘疾游客逃離場館,而也有一些殘疾游客會自己參觀,在緊急情況時行動緩慢的游客需要在工作人員的協助下完成撤離,因此在除在每個通道口配置一個工作人員,每層樓還需再配備一些備用工作人員用,行動不便的旅客撤離。
針對于是否開啟其他出口用于人員的疏散:發生恐怖襲擊后,安全人員需要在最短的時間里就位,進行人員的疏散,而游客不會等待安全人員就位后才開始撤離。因此在襲擊后安全人員通過正常通道就位難度較大。對于非日常開發的通道,僅有場館工作人員及官員知道而游客并不知道,同時絕大多數人具有從眾心理,在慌亂時不會選擇走自己不熟悉的通道。因此這些通道中的容客量會遠少于正常通道。我們還可將殘疾人員的疏散也安排進這些通道中,從而避免殘疾人員在疏散時,對他人或自己造成的不便。綜上所述非日常開放的通道中的人員構成是:場館官員、安全人員、殘疾游客、不從眾或偶然看到該出口的游客。所以安全人員在疏散人流時不主動提醒非日常開放的通道,當日常開放的通道達到飽和時,再選擇性的開放出口以供游客疏散。
參考文獻
[1] BRAGLIA M, CASTELLANO D, GABBRIELLIR.基于博弈論的應急出口選擇新模型.Advancesin Complex Systems, 2013.
[2]Helivaara S,Kuusinen J M, Rinne T,et a1.通道疏散中行人運動與出口選擇的研究[Jl. Safetyseience, 2012, 50(2): 221-227.
[3]Oliveira dos Santos Soares R, Martinez A S.空間囚徒困境中合作演化的幾何模式:一種群體內模式[J]。《物理A》:統計力學及其應用,2006,369(2):823-829.
[4]Helbing D.人群自組織理論[M]//社會自組織理論Springer Berlin Heidelberg,2012:71-99.
[5]劉潤然,賈春曉,章劍林等,年齡相關的生命力對于囚徒困境博弈合作頻率之提升[J].《物理A》:統計力學機器運用,2012,391(18):4325-4330.
[6]Goldengorin B, Krushinsky D, MakarenkoA,大規模人群的同步運動問題//非線性動力學與同步的最新進展Springer Berlin Heidelberg,2009: 227-303
[7]孟園,基于多Agent的大型公共建筑人員應急疏散微觀特征分析與仿真研究,2016.6.

