“問”出精彩

黃琴琴

摘要：在數學教學中，課堂提問既是重要的教學手段，又是完美的教學藝術。教師科學地處理好何時提問、提什么問題、怎樣提問等環節，可以幫助學生把握重點、化解難點，培養思維能力。筆者通過概念課“方程的根與函數的零點”教學為例，闡述對“有效的課堂提問”的一些思考與感悟。

關鍵詞：高中數學;課堂提問;有效性

“課堂提問”是指在課堂教學活動中，為完成一定的教學任務，緊扣教學重點、教學難點、學生情況等而設計出的一系列的問題。它是教師與學生以問題為中介進行正常教學的有效方法和手段。有效的課堂提問是激發學生積極思維的發動機，是開啟學生智慧之門的鑰匙;能夠調動學生的積極性，從而構建高效的數學課堂，提高課堂教學效率，使學生真正有所收獲。

在《普通高中數學課程標準》中，對于數學學科的基本理念有這樣的設定：高中數學教學以發展學生數學學科核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質。其中關鍵詞“創設"、“啟發”、“引導”的落實，要依靠教師根據教學的實際情況創設的有效課堂提問。

筆者參加了2018年新疆高中青年教師優秀課展評，本文是根據課堂教學大賽中參評課“方程的根與函數的零點”教學的片段：探索“零點存在的條件”為例，來闡述對“有效課堂提問”的感悟。參賽者以人教A版必修1練習題為依據，結合新疆四月的氣溫變化特點創設問題情境，設計課堂提問，引導學生發現函數零點存在的條件。

一、課堂呈現與問題評析

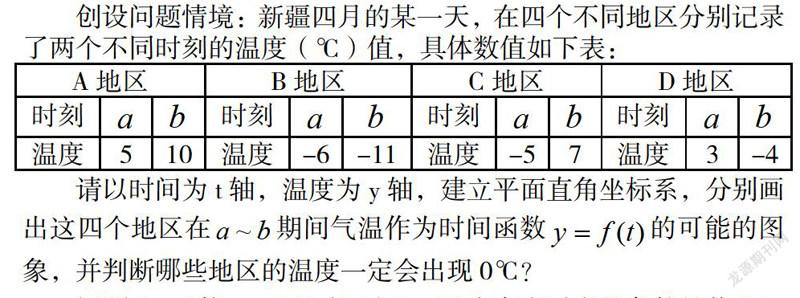
創設問題情境：新疆四月的某一天，在四個不同地區分別記錄了兩個不同時刻的溫度（9C）值，具體數值如下表：

請以時間為t軸，溫度為y軸，建立平面直角坐標系，分別畫出這四個地區在a～b期間氣溫作為時間函數y=f（t）的可能的圖象，并判斷哪些地區的溫度一定會出現0C？

問題1：函數y=f（t）在區間（a，b）內存在零點的條件是什么？問題評析：以新疆四月的氣溫變化特點引出問題，易于讓學生產生興趣，使學生自愿的參與到問題的探究當中。而且這個問題以學生的經驗為基礎，并帶有一定的趣味性和開放性，留給學生充分的發揮空間，對突破教材的難點有重要的意義。而且氣溫關于時間的函數是一個連續的函數，為學生后繼發現零點存在的條件提供前期準備。

通過問題1學生發現了C、D地區溫度一定會出現0C，也就是這兩地區的溫度函數圖象都存在零點，兩端點的函數值異號，也就是f（a）.f（b）《0。但溫度關于時間的函數是一個特殊的函數，想要發現函數零點存在的條件需要把溫度關于時間的函數y=f（t）推廣到一般的函數y=.f（x）。進而提出問題2。

問題2：若f（a）.f（b）《0，則函數y=f（x）在區間（a，b）內一定有零點嗎？

問題評析：問題是加速器，加快學生思維的發展。問題2讓學生經歷從特殊到一般的過程。使學生思考函數圖象是否有其它情形，為學生理解零點存在性的判定方法打下基礎。

學生通過小組討論認識到函數圖象還有不連續的情況，當函數圖象在區間（a，b）內斷開時，即使函數滿足f（a）.f（b）《0，但函數y=.f（x）在區間（a，b）內可能沒有零點。以兩個問題為推動力，推動學生發現了函數y=f（x）在區間（a，b）內存在零點的兩個條.件，此時教師順勢給出零點存在性定理：

如果函數y=f（x）在區間【a，b】上的圖象是連續不斷的一條曲線，并且有f（a）.f（b）《0，那么，函數y=f（x）在區間（a，b）內有零點，即存在c∈（a，b），使f（c）=0，這個C也就是方程f（x）=0的根。

為了能使學生更深層次地理解定理，教師又追加了兩個課堂提問：

問題3：若函數y=f（x）在區間【a，b】上連續，且f（a）.f（b）>0，則f（x）在區間（a，b）內就一定沒有零點嗎？

問題4：滿足零點存在定理能確定函數y=f（x）在區間（a，b）內零點的個數嗎？

問題評析：“問題為核心”永遠是教師的教學原則和執行標準。在教學中，教師設計的問題都應該圍繞知識點的生成和發展過程，圍繞概念怎么發生、怎么形成、怎么再現，來促進學生弄清楚三個“什么”一是什么、為什么、還有什么。問題3、4的設計就是為了進一步幫助學生鞏固和深化對零點存在性定理的理解。

二、對“有效的課堂提問”的思考與感悟

課堂提問是一項設疑、激趣、引思的綜合性教學藝術，課堂提.問成功與否，直接關系到單位時間內教育教學的效果。因此，教師必需加強自身綜合素質的培養，發揮好課堂提問的效能。

有效的課堂提問應該具有如下特征：（1）問題的表述要簡潔明了，用詞規范。提問的措辭要簡單，不能有歧義。（2）問題的范圍要確定。教師所提問題要指向明確，這樣學生才知道從哪方面作答，但若問題的范圍太廣的話，學生則無從答起。（3）問題要難易適度，注意問題的科學性。好的問題應基于學生的實際學習情況，深人淺出，要考慮到學生的接受程度、知識范圍和思維能力。（4）問題要優選，問在知識關鍵處;選準時機，問在教學當問處。適時，即掌握提問時機，就是教師要善于利用或創設一個最佳時間。如果提問早了，學生認知結構或思維過程上出現斷層，欲速則不達。問遲了，會使提問失去了促進學生思維，發展學生思維的作用。

問題是數學的心臟。陶行知說“發明千千萬，起點是一問。禽獸不如人，過在不會問。智者問得巧，愚者問得笨”。巧妙的提問，如一條紐帶，架起師生交流的橋梁，將師生的認識、情感緊密相連。要做到有效的課堂提問，教師就應不斷學習，深鉆研，勤思考、多分析、努力優化課堂發“問”，“問”出學生的思維，“問”出學生的創造，“問”出高效課堂。

參考文獻：

【1】中華人民共和國教育部。普通高中數學課程標準（2017年版）【M】。北京：人民教育出版社，2018。

【2】陳中峰。論數學學科過程性知識的教與學。福州：福建教育出版社，2016。

【3】中華人民共和國教育部。中學數學教學參考。陜西：陜西師范大學出版社，2018。