歸類練習(xí) 提升能力
李生軍

【關(guān)鍵詞】 數(shù)學(xué)教學(xué);練讀;歸類
【中圖分類號(hào)】 G623.5
【文獻(xiàn)標(biāo)識(shí)碼】 A
【文章編號(hào)】 1004—0463(2019)
13—0170—01
“長(zhǎng)方形周長(zhǎng)”是小學(xué)數(shù)學(xué)三年級(jí)上冊(cè)的教學(xué)重點(diǎn),根據(jù)本人對(duì)長(zhǎng)方形周長(zhǎng)的教學(xué)實(shí)踐研究,將長(zhǎng)方形周長(zhǎng)的題型歸納為七類,具體如下:
一、移
通過(guò)向上、向下、向左或向右平移的方法,將一個(gè)不規(guī)則圖形變成規(guī)則的長(zhǎng)方形或正方形,再求周長(zhǎng)。
例如,下圖是游樂(lè)園的平面圖,A處為進(jìn)出口,小杰繞游樂(lè)場(chǎng)走了一周,從A處進(jìn)入,又從A處出來(lái),他一共走了多少米?
分析:將這個(gè)不規(guī)則的平面幾何圖形通過(guò)向上、向左及向右平移,就得到了一個(gè)長(zhǎng)為280米、寬為260米的長(zhǎng)方形。求小杰走了多少米實(shí)際是計(jì)算長(zhǎng)方形的周長(zhǎng),即(280+260)×2=1080(米)。
二、拼
將幾個(gè)相同的正方形拼成一個(gè)大長(zhǎng)方形,求大長(zhǎng)方形的周長(zhǎng)。
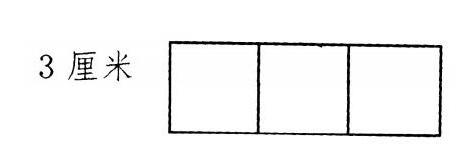
例如,將邊長(zhǎng)是3厘米的3個(gè)正方形拼成一個(gè)大長(zhǎng)方形,大長(zhǎng)方形的周長(zhǎng)是多少厘米?
分析:
(1)把完全一樣的小正方形拼成一個(gè)大正方形,每拼一次就減少了兩條邊長(zhǎng),三個(gè)小正方形拼成大長(zhǎng)方形,拼了兩次,就減少了4條邊長(zhǎng),拼成長(zhǎng)方形的周長(zhǎng)就是8條邊長(zhǎng)的和,即3×8=24(厘米)。
(2)拼成大長(zhǎng)方形后,長(zhǎng)方形的長(zhǎng)為3×3=9(厘米),寬為3厘米,那么長(zhǎng)方形的周長(zhǎng)就為:(9+3)×2=24(厘米)。
三、剪
將一長(zhǎng)方形的四角剪去4個(gè)相同的小正方形,求剩余圖形的周長(zhǎng)。
例如,已知一個(gè)長(zhǎng)方形的長(zhǎng)為10? 厘米,寬為8厘米,在四角剪去4個(gè)邊長(zhǎng)為2厘米小正方形(如右圖所 示)后剩余部分的圖形周長(zhǎng)是多少?
分析:雖然長(zhǎng)方形的四個(gè)角都剪去了邊長(zhǎng)為2cm的正方形,但通過(guò)平移以后,仍然是長(zhǎng)方形,剩余部分的周長(zhǎng)就是求原長(zhǎng)方形的周長(zhǎng),即(10+8)×2=36(厘米)。
四、跑
沿長(zhǎng)方形或正方形運(yùn)動(dòng)場(chǎng)跑幾圈,求一共跑了多少米。
例如,學(xué)校運(yùn)動(dòng)場(chǎng)跑道(如圖)長(zhǎng)120米,寬80米,小強(qiáng)沿著跑道 跑了3圈,一共跑了多少米?
分析:先要弄清楚跑道是長(zhǎng)方形,跑一圈就是求長(zhǎng)方形的周長(zhǎng),三圈就是長(zhǎng)方形周長(zhǎng)的3倍,即(120+80)×2×3=1200(米)。
五、圍
沿一面墻用籬笆圍成一個(gè)長(zhǎng)方形或正方形,求所用籬笆的長(zhǎng)度。
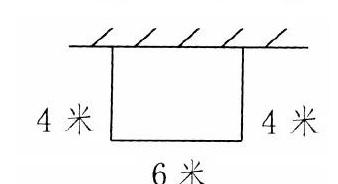
例如,淘氣想靠墻圍城一個(gè)長(zhǎng)方形的蔬菜園,長(zhǎng)是6米,寬是4米。可以怎樣圍?分別需要多長(zhǎng)的圍欄?(如下圖)
分析:靠墻圍一個(gè)長(zhǎng)方形,一種圍法是長(zhǎng)6米的一邊靠墻,即圍欄的長(zhǎng)度是:4×2+6=14(厘米);另一種圍法是寬4米的一邊靠墻,即圍欄的長(zhǎng)度是:6×2+4=16(厘米)。
六、截
在長(zhǎng)方形內(nèi)截取一個(gè)最大的正方形,求正方形的周長(zhǎng)和余下圖形的周長(zhǎng)。
例如,一張長(zhǎng)方形鐵皮,長(zhǎng)25分米,寬15分米。從這張鐵皮上截取一個(gè)最大的正方形,這個(gè)正方形的周長(zhǎng)是多少分米?余下圖形的周長(zhǎng)是多少分米?
分析:弄清楚截取正方形的邊長(zhǎng)實(shí)際上是長(zhǎng)方形的寬15分米, 即正方形的周長(zhǎng)為15 ×4=60(分米)。余下圖形的長(zhǎng)是25-15=10(分米),寬不變,仍然是15分米。即余下圖形的周長(zhǎng)為(10+15)×2 =50(分米)。
七、變
將一個(gè)平面幾何圖形變換成另一個(gè)平面圖形,求變換后圖形的邊長(zhǎng)。
例如,如右圖,如果將這個(gè)正方形的鐵絲展開(kāi),再圍成一個(gè)長(zhǎng)12厘米的長(zhǎng)方形,那么長(zhǎng)方形的寬是多少厘米?
分析:將正方形變換成長(zhǎng)方形,雖然形狀發(fā)生了變化,但圖形的周長(zhǎng)沒(méi)有變,即正方形的周長(zhǎng)就是長(zhǎng)方形的周長(zhǎng),那么長(zhǎng)方形的寬就為:10×4÷2-12=8(厘米)。
實(shí)踐證明:通過(guò)這樣的歸類練習(xí),既提升了學(xué)生對(duì)數(shù)學(xué)學(xué)習(xí)的趣味性,又讓學(xué)生學(xué)得懂、學(xué)得活,從而取得了事半功倍的教學(xué)效果。
編輯:謝穎麗

