單元教學視角下數學公式證明方法的選擇

【摘 要】對數學公式的證明的教學重點不在于用了多少種不同的方法，也不在于所用的方法有多么巧妙，而是在于要選擇合適的證明方法。數學公式證明方法的選擇要關注三個方面：一是要植根于單元內容，二是要凸顯認知的一致性，三是要追求動態發展。數學公式證明中所采用的方法應植根于單元內容，為實現單元教學的目標服務。

【關鍵詞】單元教學;數學公式;證明方法;選擇

【作者簡介】何凱果 ，一級教師。

數學公式是對數學知識高度濃縮與提煉的結晶，從某種程度上講，學習數學的其中一個重要目的就是為了獲得更多有用的模型與公式。數學公式教學也是數學課堂教學的重要組成部分，其教學過程一般由公式的猜想與發現、推導與證明、拓展與應用三個環節構成，其中公式的推導與證明是“重頭戲”。對數學公式的證明教學要做到“不惜時，不惜力”已經成為很多教師的共識，教師希望通過讓學生親歷公式推導與證明，從而達到“知其然而知其所以然”的效果。

數學知識間的聯系性決定了公式證明方法的多樣性，單從某節課看，由于缺乏明確的宏觀目標導向，證明方法的選擇已經成為很多教師的一大困惑。但如果站在單元的視角認識教學內容，連貫地理解教學目標，使教學的方向性得到進一步明確，將公式證明活動的每一步、每一個環節都放到單元教學活動的大系統中考量，而不是片面地突出或者強調某一知識點，那么，公式證明的方法必然會清晰起來。

一、證明方法應植根于單元內容

現行的數學教材是以知識系統為主線來組織單元教學內容的，比如，函數單元、數列單元、解析幾何單元等，這樣做的好處就是在遵循學科自身邏輯特點的基礎上為學生提供相對完整的數學認知。數學公式是單元內容的重要組成部分，證明中所采用的方法不僅不能偏離單元的主題，而且應該植根于單元內容，為實現單元教學的目標服務。

例如，在推導“兩角差的余弦公式”中，人教A版2007年版的教材（以下簡稱教材）提供了兩種方法。一是幾何構造法，如圖1，在單位圓內構造直角三角形 ，用割補的方法得到OM=OB+BM=OB+CP=OAcosα+APsinα=cosβcosα+sinβsinα;二是向量法，聯想到α，β終邊與單位圓的交點分別為 A（cosα，sinα），B（cosβ，sinβ），發現等式cos（α-β）=cosαcosβ+sinαsinβ的右邊與向量數量積公式的坐標表示 a→·b→=x1x2+y1y2相近，從而聯想到OA·OB=cos（α-β）=cosαcosβ+sinαsinβ。幾何構造法比較直觀，但學生很難想到;向量法比較簡單，但似乎與三角函數沒什么聯系，因此，很多教師對選擇哪種方法感到很糾結。其實選擇哪種方法，關鍵在于對“兩角差的余弦公式”這節內容所屬的單元主題的認識。

圖1

教材是按照“三角函數—平面向量—三角恒等變換”順序來編寫的，因此，這節內容既是“三角函數”內容的延續，又是“平面向量”應用價值的體現。因此，公式的證明方法既要凸顯“三角函數”單元主題，又有體現向量的工具作用。基于這樣的分析，采用向量法是比較合理的，當然，最后還需要把證明結論推廣到任意角。如果教材按照“三角函數—三角恒等變換”的順序來編寫，那么，上述兩種方法就都不合適了。因為它們都沒有凸顯“三角函數是圓函數，兩角差的余弦公式是圓對稱性的體現”這一單元主題，而旋轉對稱法恰恰能夠滿足主題要求：如圖2，P1（cosα，sinβ），A1（cosβ，sinβ），P（cos（α-β），sin（α-β）），把扇形OAP繞點O旋轉β角，則點A，P分別與A1，P1重合，根據圓的旋轉對稱，可知AP=A1P1，則[cos（α-β）-1]2+sin2（α-β）=（cosα-cosβ）2+（sinα-sinβ）2，可得cos（α-β）=cosαcosβ+sinαsinβ。

圖2

由此可見，教師首先要深入了解教材的編寫意圖，從而對教學內容所屬的單元有明確的定位，然后再根據單元教學的主題對公式證明方法做出合理的選擇。

二、證明方法應凸顯認知的一致性

在單元教學視角下，數學公式的證明不僅需要在學生已有認知經驗與認知規律的基礎上進行綜合考量與整體性建構，而且還需要確保同一單元內容中具有內在關聯性的公式在證明思路的呈現與證明過程的設計上體現出一致性的特點，也就是說通過類比一個數學公式的證明思路能夠順利獲得證明另一個數學公式的方法，從而實現教學邏輯內部的協調統一與有序轉化。

例如，正弦定理與余弦定理是兩個具有較強關聯性的公式。它們分別從正弦與余弦的視角對三角形的邊角關系進行定量刻畫，因為正弦、余弦可以相互轉化，所以，從某種程度上講，正弦定理與余弦定理在本質上是等價的。因此，這兩個定理的證明方法應該是一致的。在教材中，正弦定理是通過三角形作高線而獲得的，而余弦定理的證明則是借助了向量的數量積，證明方法的不一致無法揭示兩個公式之間的聯系，這不利于學生整體性認知的發展。

其實，兩個公式的證明可以做一致化處理。余弦定理其實也可以通過三角形作高線來獲得。如圖3，CD垂直于AB，則CD=bsinA，AD=bcosA，BD=c-bcosA，所以a2=CD2+BD2=b2sin2A+（c-bcosA）2=b2+c2-2bccosA。同樣地，正弦定理也可以通過向量數量積來證明，在此筆者不再贅述。當然，最后到底選擇哪種方法，還是要取決于這兩個定理所屬的單元主題。

圖3

又比如，要說明“勾股定理是余弦定理的特殊形式”，雖然這能夠從兩個公式的結構特征上得到確認，但如果無法從證明方法上得到佐證，顯然是不具備說服力的。歷史上，歐幾里得是這樣證明勾股定理的。

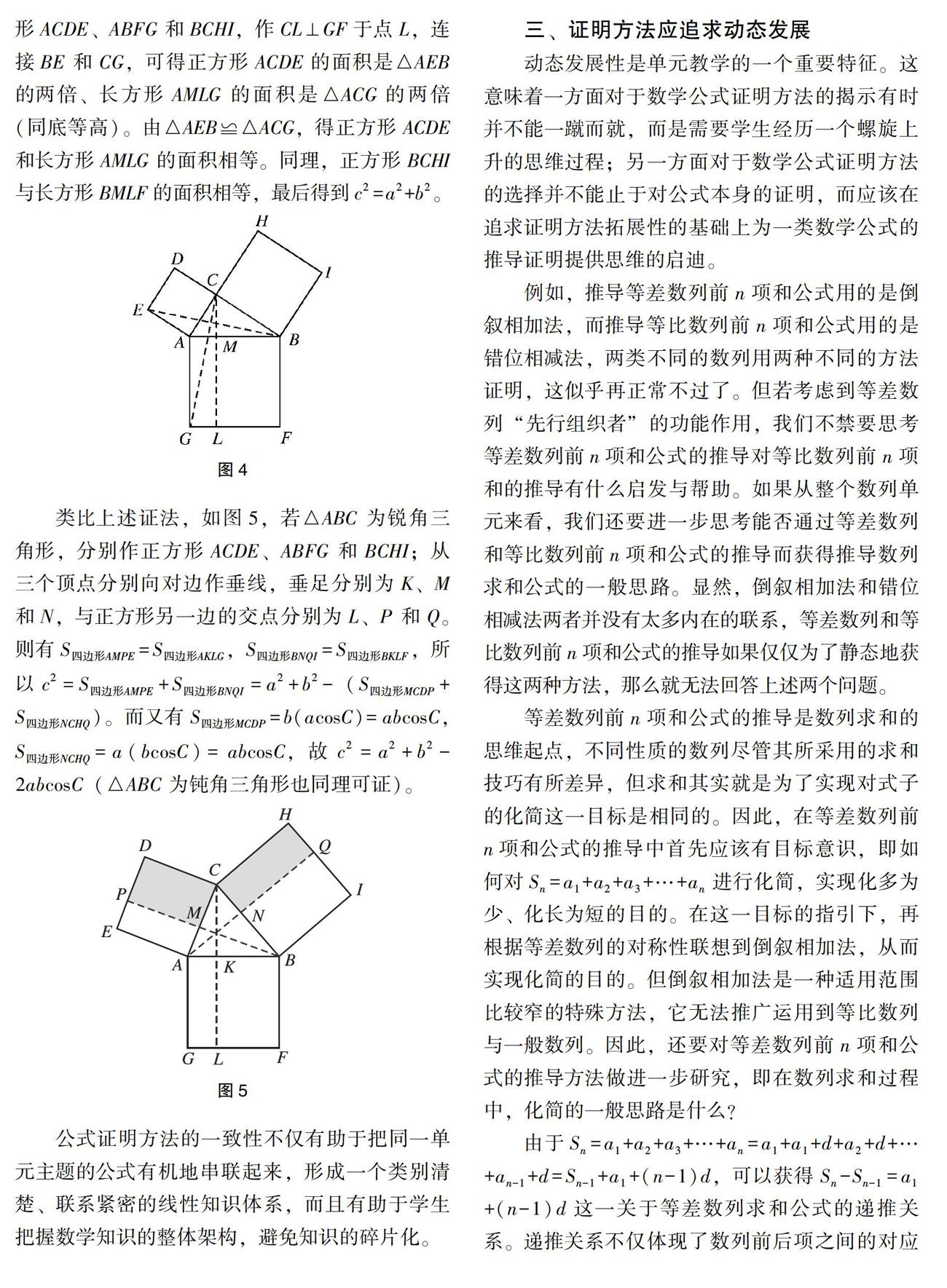
如圖4，分別在直角△ABC 的三邊上作正方形ACDE、ABFG 和BCHI，作CL⊥GF于點L，連接BE 和CG，可得正方形ACDE的面積是△AEB 的兩倍、長方形AMLG 的面積是△ACG的兩倍（同底等高）。由△AEB≌△ACG，得正方形ACDE 和長方形AMLG 的面積相等。同理，正方形BCHI與長方形BMLF的面積相等，最后得到c2=a2+b2。

圖4

類比上述證法，如圖5，若△ABC 為銳角三角形，分別作正方形ACDE、ABFG 和BCHI;從三個頂點分別向對邊作垂線，垂足分別為K、M 和N，與正方形另一邊的交點分別為L、P 和Q。則有S四邊形AMPE=S四邊形AKLG，S四邊形BNQI=S四邊形BKLF，所以 c2=S四邊形AMPE+S四邊形BNQI=a2+b2-（S四邊形MCDP+S四邊形NCHQ）。而又有S四邊形MCDP=b（acosC）=abcosC，S四邊形NCHQ=a（bcosC）=abcosC，故c2=a2+b2-2abcosC（△ABC 為鈍角三角形也同理可證）。

圖5

公式證明方法的一致性不僅有助于把同一單元主題的公式有機地串聯起來，形成一個類別清楚、聯系緊密的線性知識體系，而且有助于學生把握數學知識的整體架構，避免知識的碎片化。

三、證明方法應追求動態發展

動態發展性是單元教學的一個重要特征。這意味著一方面對于數學公式證明方法的揭示有時并不能一蹴而就，而是需要學生經歷一個螺旋上升的思維過程;另一方面對于數學公式證明方法的選擇并不能止于對公式本身的證明，而應該在追求證明方法拓展性的基礎上為一類數學公式的推導證明提供思維的啟迪。

例如，推導等差數列前n項和公式用的是倒敘相加法，而推導等比數列前n項和公式用的是錯位相減法，兩類不同的數列用兩種不同的方法證明，這似乎再正常不過了。但若考慮到等差數列“先行組織者”的功能作用，我們不禁要思考等差數列前n項和公式的推導對等比數列前n項和的推導有什么啟發與幫助。如果從整個數列單元來看，我們還要進一步思考能否通過等差數列和等比數列前n項和公式的推導而獲得推導數列求和公式的一般思路。顯然，倒敘相加法和錯位相減法兩者并沒有太多內在的聯系，等差數列和等比數列前n項和公式的推導如果僅僅為了靜態地獲得這兩種方法，那么就無法回答上述兩個問題。

等差數列前n項和公式的推導是數列求和的思維起點，不同性質的數列盡管其所采用的求和技巧有所差異，但求和其實就是為了實現對式子的化簡這一目標是相同的。因此，在等差數列前n項和公式的推導中首先應該有目標意識，即如何對Sn=a1+a2+a3+…+an進行化簡，實現化多為少、化長為短的目的。在這一目標的指引下，再根據等差數列的對稱性聯想到倒敘相加法，從而實現化簡的目的。但倒敘相加法是一種適用范圍比較窄的特殊方法，它無法推廣運用到等比數列與一般數列。因此，還要對等差數列前n項和公式的推導方法做進一步研究，即在數列求和過程中，化簡的一般思路是什么？

由于Sn=a1+a2+a3+…+an=a1+a1+d+a2+d+…+an-1+d=Sn-1+a1+（n-1）d，可以獲得Sn-Sn-1=a1+（n-1）d這一關于等差數列求和公式的遞推關系。遞推關系不僅體現了數列前后項之間的對應關系，即已知前一項可以求得后一項，而且還反映了數列自相似這一本質特征，即局部與整體在形態、功能、信息、時間、空間等方面具有統計意義上的相似性，而數列求和實際上就是借助自相似來達到結構化簡的目的。根據Sn-Sn-1=a1+（n-1）d的結構特征，可以用累和法進行化簡，得Sn=na1+（1+2+…+n-1）d，于是等差數列前n項和問題就轉化為對自然數列的前n 項求和，這就與教材中的情境引入聯系起來了。

對于等比數列前n項求和，也可以利用自相似原理進行化簡：Sn=a1+a2+a3+…+an=a1+q（a1+a2+…+an-1）=a1+qSn-1，即Sn-qSn-1=a1。一方面，從這個遞推關系中可以發現“Sn-1乘q與Sn的差是常數”，這就是錯位相減法的靈感之源;另一方面，把遞推關系與Sn-Sn-1=an聯立，可直接求得等比數列前n項和公式Sn=a1-anq1-q（q≠1）。由此可見，對于一般的數列求和關鍵是獲得蘊含自相似結構特征的遞推關系，然后再借助數列本身具有的特性實現結構上的化簡。

公式的推導證明本身就是經驗積累、思維遞進的動態認知過程，在深刻領悟證明方法共性與個性、通法與特法密切聯系的基礎上，教師要幫助學生不斷地拓展思維的深度、廣度與高度。

單元視角下的公式證明方法的選擇猶如在大森林的體系下審視每一棵樹木，可以讓教師擺脫大量眼花繚亂方法、技巧的干擾，直面單元教學目標與核心素養目標，使得公式證明教學過程前后呼應、環環相扣、邏輯分明。

（責任編輯：陸順演）