關(guān)于牛頓運(yùn)動(dòng)定律解決“臨界問題”的教學(xué)研究

楊春華

(吉林省松原市前郭爾羅斯蒙古族自治縣第五中學(xué) 138000)

人教版高中物理必修一《用牛頓運(yùn)動(dòng)定律解決問題》一節(jié)中，有一類問題一直困擾著學(xué)生，這就是 “臨界問題” ，又稱“極值問題”.常見題型如下：

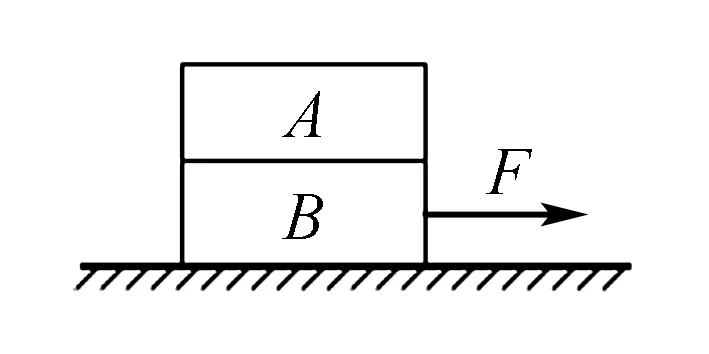
圖1

例題如圖1所示，水平地面上疊放著質(zhì)量分別為mA=2 kg，mB=3kg的A、B兩木塊，處于靜止?fàn)顟B(tài).A與B間的動(dòng)摩擦因數(shù)μ1=0.2，B與地面間的動(dòng)摩擦因數(shù)μ2=0.1.若用水平拉力F向右拉木塊B，使之從A與地面間抽出來，已知重力加速度為g，則拉力F的最小值為( ).

A．4N B．5N C．9N D．15N

若想解決這個(gè)問題，就要對(duì)物體間的摩擦力和各個(gè)物體運(yùn)動(dòng)狀態(tài)進(jìn)行細(xì)致分析，還要應(yīng)用牛頓第二定律把受力和運(yùn)動(dòng)狀態(tài)結(jié)合起來.學(xué)生對(duì)“最小值”的理解，很難找到突破點(diǎn)，種種因素加在一起，使得這類問題成為難題.

在實(shí)際教學(xué)中，通過對(duì)學(xué)生常見問題的匯總和課堂反饋，我認(rèn)為對(duì)學(xué)生進(jìn)行恰當(dāng)?shù)囊龑?dǎo)，找到臨界條件是解決問題的關(guān)鍵，以上面的例題為例，我的具體做法如下：

接下來就是如何應(yīng)用牛頓第二定律找到加速度a與所求外力F之間的關(guān)系了.我先采用“隔離法”對(duì)兩個(gè)木塊分別受力分析(如圖2所示)，假設(shè)兩木塊已經(jīng)出現(xiàn)“相對(duì)運(yùn)動(dòng)”，各自列出牛頓第二定律方程如下：

圖2

由以上兩式可知：當(dāng)A、B兩木塊相對(duì)運(yùn)動(dòng)時(shí)，aA是確定的，而aB大小隨拉力F的增大而增大，當(dāng)aB>aA時(shí)兩物體相對(duì)運(yùn)動(dòng)，所以拉力出現(xiàn)極值時(shí)，剛好aB=aA，解得F=15N.

圖3

以上“隔離法”分析每個(gè)物體，學(xué)生很容易理解當(dāng)加速度a不等時(shí)二者出現(xiàn)相對(duì)運(yùn)動(dòng)，加速度a剛好相等時(shí)是“臨界”狀態(tài)，學(xué)生便能總結(jié)出臨界條件，也就能獨(dú)立解決此問題，這是采用“隔離法”的最大優(yōu)勢(shì).

有了上述理論基礎(chǔ)，接下來我再?gòu)摹罢w”角度引導(dǎo)學(xué)生分析，對(duì)A、B兩木塊未發(fā)生相對(duì)運(yùn)動(dòng)前的整體受力分析(如圖3所示)，并列出牛頓第二定律方程如下：

綜上所述，我提倡在實(shí)際教學(xué)中先使用“隔離法”解決此類問題，雖然過程中涉及的力較多，但很容易讓學(xué)生明白決定兩物體是否發(fā)生相對(duì)運(yùn)動(dòng)的物理量是加速度a，而不是速度v，這樣才能和牛頓第二定律聯(lián)系起來.同時(shí)，通過對(duì)每個(gè)物體的受力分析，還能確定不受外力F作用的物體存在最大加速度，這也是使用“整體法”快速解決此類問題的前提和基礎(chǔ).可以說“隔離法”是拋磚引玉，起到了“解惑”和“鋪墊”的作用，是最終提煉出此類問題解法的重要環(huán)節(jié)，在教學(xué)中不可缺少.而且，以上講解過程循序漸進(jìn)、環(huán)環(huán)相扣，逐步突破難點(diǎn)，通過啟發(fā)引導(dǎo)學(xué)生把抽象的物理過程量化，易于學(xué)生接受，這對(duì)學(xué)生來說是很重要的.作為物理教師，首要的是教會(huì)學(xué)生“理”，其次是方法，這樣才能培養(yǎng)學(xué)習(xí)能力，萬萬不能直接告訴學(xué)生一個(gè)問題的解法，那樣只會(huì)扼殺學(xué)生的靈性，對(duì)物理的學(xué)習(xí)極為不利.我在教學(xué)中很重視對(duì)學(xué)生能力的培養(yǎng)，以上的教學(xué)研究就是一個(gè)典型實(shí)例，取得了良好的教學(xué)效果.