數學直觀想象核心素養在高考中的考查
楚利平


【摘要】縱觀近幾年的高考試題,在選擇題的壓軸題部分和解析幾何試題中,考查圖形對稱性的題目居多.這些題目能夠很好地考查學生直觀想象、數學抽象和邏輯推理的核心素養,培養學生求簡求美的意識.
【關鍵詞】直觀想象;對稱性;核心素養
1 以函數為載體考查直觀想象和數學抽象的核心素養
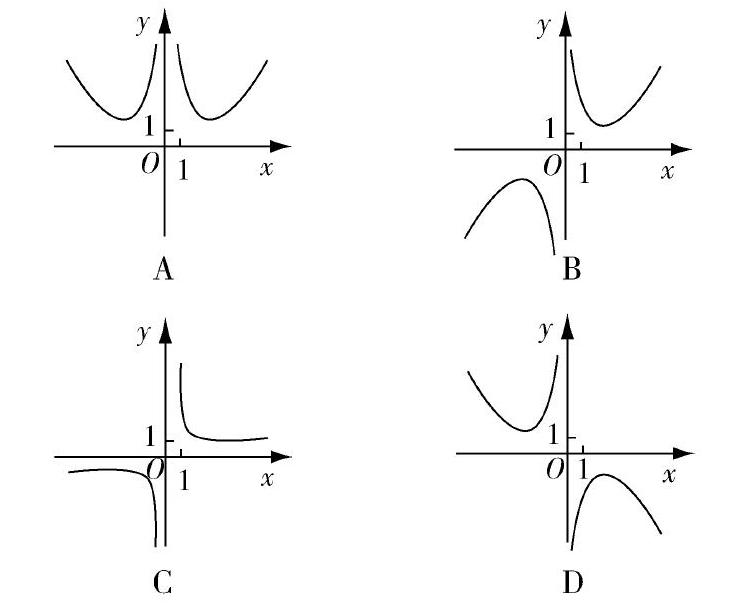
1.1 通過函數解析式,尋找對應的函數圖像
1.2 以函數為背景,綜合考查函數圖像的對稱性
反思總結 這類題目在高考中多為壓軸題,用以增加試題的難度和區分度.試題中蘊含著數形結合的思想,綜合考查了學生分析問題和解決問題的能力,對學生數學抽象和直觀想象的核心素養要求較高,利用函數圖像的對稱性可以使問題得以快速解決.因此我們在課堂教學中必須滲透直觀想象和數學抽象的核心素養,結合教學內容,把函數的解析式和函數的圖像有機統一起來,并在課堂教學中注意運用現代化的教育技術,借助函數圖像使抽象的數學問題直觀化,培養學生的數學抽象和直觀想象的核心素養.
2 在解析幾何中考查圖形的對稱性
2.1 試題在呈現時就突出了幾何圖形的對稱性,引導學生解題方向
反思總結 解決本題的核心就是要抓住橢圓關于x軸對稱這一隱藏信息,這是研究圓錐曲線的基本常識.題目以橢圓的左頂點為基點,告知|AM|=|AN|,引導學生思考△AMN關于x軸對稱,再利用∠MAN=90°,就可以得到直線AM的斜率為1,使問題獲解.
2.2 對稱性隱含在解題過程中的題目
反思總結 本題第一問實質是北師大版選修1-1習題2-1第7題的改編,在解決第二問時利用了橢圓和直線y=x關于原點成中心對稱圖形, 這時在解題中常設P(x0,y0),Q(-x0,-y0),極大地簡化了運算過程.由于字母較多,學生不容易找到對應關系,巧妙地利用了-x0和xG是方程①的兩個解,由根與系數關系得到xG=x0(3k2+2)[]2+k2,使問題簡化,這在解析幾何中是一種常用手法.鑒于圓錐曲線的對稱性在高考中的考查非常廣泛,所以在圓錐曲線性質研究的教學中,我們必須向學生強調對稱性的重要性,要求學生掌握利用方程研究對稱性的方法,掌握利用對稱性畫圓錐曲線的方法,引導學生把圓錐曲線的圖像和圓錐曲線的方程有機統一起來,在探討圓錐曲線的性質和圓錐曲線與直線的位置關系時注意利用圖像的直觀性簡化運算,樹立求簡意識.
通過以上分析,可知關于對稱性的考查,以高考壓軸題形式出現居多,這就要求我們必須重視知識的發生、發展過程, 引導學生自己探究、領悟和掌握研究問題的過程和數學思想方法,提升學生的數學核心素養,同時在課堂教學中重視數學基本思想和基本方法的滲透,強化“四基、四能”,注重提升學生的數學核心素養.例如,在必修1的教學中要加強函數與函數圖像的有機聯系,滲透數形結合的思想,在研究函數的性質時,注意利用函數圖像的直觀性引導學生理解函數的單調性、對稱性;在必修2的教學中,以旋轉體和圓為載體進一步加強學生對圖形對稱美的理解和感悟,提升學生直觀想象的核心素養;在必修4的教學中,首先利用單位圓研究正弦函數的性質,其次利用單位圓的對稱性研究三角函數的誘導公式和周期,感悟圖形的直觀性,最后利用函數y=Asin(ωx+φ)+k的圖像及其變化讓學生進一步體會和感悟圖形的對稱美,利用圖像引導學生認識函數的最值、單調性、周期性、對稱性,進一步培養學生直觀想象的核心素養;在選修教材圓錐曲線的教學過程中,利用橢圓和雙曲線的軸對稱和中心對稱的性質,以及拋物線的軸對稱素材讓學生充分體會對稱美在數學學習中的重要地位,同時讓學生掌握運用代數方法研究圓錐曲線性質的方法,了解對稱性在解決問題時的簡潔性,培養學生求簡求美意識,不斷地提高學生直觀想象的核心素養.
【參考文獻】
[1]中華人民共和國教育部.普通高中數學課程標準(2017年版)[M].北京:人民教育出版社,2018.

