關于類比思想在初中數學教學中的實踐與探索

劉志娟

[摘? 要] 文章介紹了類比思想的意義，并以多個例題呈現(xiàn)了類比思想的應用方式，以及滲透類比思想的教學建議，進而增強學生的類比意識，培養(yǎng)學生的創(chuàng)新能力.

[關鍵詞] 初中數學;類比思想;滲透

素質教育要求教師不僅需要傳授給學生知識技能，更需要培養(yǎng)他們的思維能力. 類比是合理推理的一種，它也是創(chuàng)新的一種重要手段. 類比的出現(xiàn)為學生研究問題建構了一定的思維框架，找尋到具有創(chuàng)新性的解題方法，架起了知識與方法之間的橋梁，激活了學生的思維. 因此，類比思想的滲透是數學教育的核心內容之一. 事實上，教材中也多處涉及類比思想的教學. 現(xiàn)實教學中，不少教師也有意識地進行了類比思想的滲透，卻無法有序系統(tǒng)地進行. 本文將簡述類比思想的意義，并結合案例闡述其應用方法，以及滲透類比思想的教學建議，與同仁分享.

類比思想的意義

1. 促進數學的發(fā)展

縱觀數學發(fā)展的過程，每一項重大發(fā)現(xiàn)都離不開數學思想的推動與創(chuàng)新，而類比思想在數學發(fā)展史中起到了十分重要的作用，如波利亞通過類比法的合理運用從而在學科研究中發(fā)揮了其能力;著名科學家牛頓正是類比天體運動和自由落體運動而發(fā)現(xiàn)了萬有引力;又如著名生物學家達爾文類比植物的自花受精和人類的近親結合進而得出自己子女病態(tài)的根源. 因此，正是在這個意義上，盡管在數學研究方法和手段繁多的今日，類比思想仍然是數學教學與解題中的一種有效手段.

2. 培養(yǎng)學生的創(chuàng)造力

隨著新課改的推進，教學已經不再局限于數學知識的傳授，學生創(chuàng)造能力的培養(yǎng)已成為教師追求的綜合教學目標. 這就要求教師在教學的過程中樹立全新的教學理念，有意識地啟發(fā)學生的求知欲望，充分挖掘數學本質，關注學生數學思想的滲透，致力于學生創(chuàng)造性的培養(yǎng). 類比思想是孕育學生數學創(chuàng)造的“孵化器”，學生的一個又一個“微創(chuàng)”都源于類比思想. 在類比過程中，學生會主動進行觀察、猜想、思維、推理，不斷促進新思路的形成，從這個意義上來說，類比思想是一種創(chuàng)新的思想. 在教學的過程中，類比的重要性體現(xiàn)在思維的啟迪，從類比中找尋到解決問題的突破口，完善解題路徑. 相較于歸納與演繹，類比更有助于創(chuàng)新，當歸納法和演繹法無法突破時，它往往能另辟蹊徑，達到“柳暗花明”的境界.

類比思想的應用方式

1. 低維與高維的類比

例1? ?（1）如圖1，已知C，D，E，F(xiàn)為線段AB上的點，試求出圖中線段的條數.

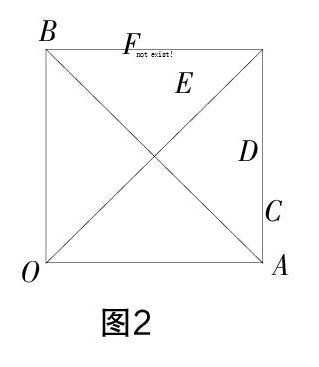
（2）如圖2，已知OA，OB，OC，OD，OE，OF為過同一點O的射線，試求出圖中角的個數.

分析? 一般情況下求線段的條數，我們是通過確定一個端點，再確定另一個端點的方法來完成的. 觀察圖1可以看出一共有6個點，可以確定的線段條數為5條，且每條線段都重復一次，列式為：5+4+3+2+1=15，故共有線段15條. 類比直線中的線段來求平面內的角，也就是每個角的兩邊對應線段兩個端點，從而建構了共同之處，則列式為：5+4+3+2+1=15，故共有角15個. 在給出平面內角的問題時，回憶直線上的線段問題，讓類比物呈現(xiàn)得更清晰，更大程度上讓類比發(fā)生.

因此，在教學過程中宜采用類似問題情境，激活學生的聯(lián)想，促進類比的發(fā)生，從而化難為簡，啟迪學生的思維，找尋到解決問題的有效途徑.

2. 數與形的類比

初等數學可以分為代數與幾何，常見的類比有數形結合、函數與圖像等. 眾所周知，數與形之間的關系是相互依存的，我們在教學中既要啟發(fā)學生通過“形”來探究“數”，又需引導學生利用“數”來研究“形”.

例2？搖 已知■=■=■=k，試求出k的值.

分析? 不少學生在解決本題時習慣性運用等比定理進行求解，而事實上，若從聯(lián)想兩條直線重合這一條件出發(fā)進行數與形的類比，則可以使問題得到更好的解決.

據題意，已知條件可以類比為直線ax+by=c①和直線（b+c）x+（c+a）y=a+b②，直線①與直線②重合，①+②可得（a+b+c）（x+y）=a+b+c. 當a+b+c≠0時，可得x+y=1. 它與①為同一條直線，則a=b=c，所以k=■=■，則k=-1或k=■.

3. 有限與無限的類比

數學中經常會涉及有關無限問題的解決，而大部分無限的性質都可由有限問題進行類比而得. 因此，在探究無限情況下的問題時，首先可以想方設法找尋到與之相關的有限問題，然后再將有限情形下的解決方法和結論類比解決無限問題.

例3？搖 證明：正多邊形的面積為周長與邊心距乘積的一半.

分析? 本題可以類比有限情形下，如“三角形的面積為底與高的乘積的一半”這一結論進行求證，從而證實這一結論的正確性. 當然，在解決有限與無限的類比中，由于二者之間存在著本質上的區(qū)別，常常會暗藏較多的“陷阱”，如若類比得不夠準確，常常會導致錯誤的發(fā)生. 因此，類比可以為數學探究指明方向，但并不是完全的可靠，在進行類比時還需進一步思考類比的合理性問題.

滲透類比思想的教學建議

1. 創(chuàng)設情境，熏陶類比思維

興趣是學習的內驅力，而有效教學情境的創(chuàng)設是充分激趣的最佳方式. 傳統(tǒng)的數學教學，教師往往直接設問，其結果是無法激發(fā)學生數學學習的主動性. 其實，教師在進行教學設計時，更多的應該站在問題的源泉處，通過介紹類比的重大作用，如伽利略的拋物實驗、計算機的誕生等等，從而激發(fā)和鼓勵學生大膽類比，使之創(chuàng)造性地發(fā)現(xiàn)問題. 只有這樣，數學課堂才是有效的.

例如，教學“反證法”，可以引入推理故事“路邊苦李”這個人人熟知的感性素材進行類比，為反證法步驟的及時性總結和合理性理解奠定了良好的基礎，同時也在一定程度上闡釋了反證法的實用價值，使學生對數學倍增親切感，從而讓學生形成創(chuàng)新思路.

2. 創(chuàng)新教學方式，強化類比意識

數學教學的過程也就是經驗改造的過程，在類比思想滲透的過程中，教師需通過教學方式的創(chuàng)新，給予學生充足的時間進行思考，讓學生積極尋找類比物，在類比的過程中充分發(fā)揮自身的引導作用，使學生受到強烈的感染，進一步增強他們的數學意識，體會數學活動的樂趣，從而強化類比意識. 學生在不斷地經歷大大小小的類比的過程中逐步積淀類比經驗，學會數學的思維.

綜上所述，類比思想在解決數學問題當中起到了十分重要的作用，較強的類比能力成就了偉大的科學發(fā)明，推動了數學的進步和發(fā)展. 在初中數學教學中應用類比思想去發(fā)現(xiàn)和解決問題的例子比比皆是，因此，我們數學教師需及時捕捉各種類比念頭，牢牢把握二者之間的相似之處，在不斷地過渡信息和不斷地證明中，使其科學化，從而使學生的創(chuàng)造能力在一個又一個的類比實踐中得以升華.