猜想—驗證，有助于培養學生的高階思維

胡艷英

【摘 ? 要】數學“證明”的技能并非要到中學才開始培養，小學中高段教學即可逐步嘗試和滲透。通過運用“猜想—驗證”的方式來進行教學，既可以在學生心中埋下“證明”的種子，也有利于培養學生的高階思維能力。

【關鍵詞】小學數學;教學;培養高階思維

在小學階段，教師應設法讓學生提出自己的觀點并進行佐證，有理有據地說出自己的想法、做法，得出相對應的結論。這樣的訓練可以促使學生的思維更加嚴謹，有深度。

一、臆測教學的啟示

臺灣清華大學林碧珍教授倡導的小學數學臆測教學，其基本理念就是“有多少證據說多少話”。學生在學習新知識時，會在教師的引導下經歷“造例—提猜想—效化—一般化—證明”這一系列學習過程，積累豐富的學習經驗。

（一）案例再現：“圓的面積計算”

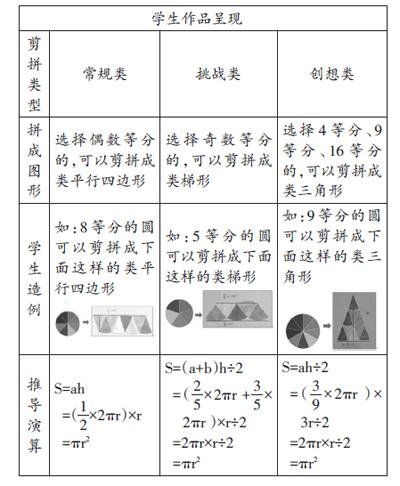
關于圓面積公式的推導，林碧珍團隊的教師花了四節課的時間進行實踐。執教教師為學生提供了等分成不同份數的圓形紙片，供學生選擇進行探索造例，用已學過的平行四邊形、梯形、三角形的舊知來計算出圓的面積。

圓形紙片等分的情況有如下幾種：3等分，4等分，5等分，6等分，7等分，8等分，9等分，10等分，13等分，16等分。

學生選擇上述一種進行剪拼研究，拼成已學過的圖形，嘗試計算出圓的面積，然后在小組內進行交流。

小組派代表將猜測的結論在全班同學面前闡述。最后，教師對每一種猜想進行引導剖析。學生發現每一種情況最終都會用“半徑×半徑×3.14”來計算，從而得出圓面積的計算公式。研究到此并未結束，教師接著拋出問題：什么時候可以拼成大三角形來計算，有個數限制嗎？個數有什么特征？引導學生發現，只有當一個圓平均分成完全平方數的個數時，大三角形才可拼成。

（二）觀課啟示

從“學習效果”的角度看，學生完全投入新課的學習之中，每個人都有自己的想法和收獲，在分享自己觀點的同時也吸納別人的不同方法，學習這件事情在每個學生身上真實地發生。雖然學習過程看起來緩慢，但學生親歷其中，人人思考，參與猜想，見證了知識的形成。在這節課中深深體會到學生是探索的主體，教師是“顧問”和“引路人”。

從“學習方法”的角度看，每個學生都有自己的選擇權，選擇自己喜歡的學習材料，剪拼成自己喜歡的熟悉的圖形來探究，沒有強制性規定，沒有單一式灌輸。在學習過程中，學生有豐富的想象空間，他們按自己的想法剪拼成類平行四邊形、類梯形和類三角形，都近似地計算出圓的面積。最后歸納導出圓的面積計算公式是“S=πr2”。

由此可見，對于小學中高段學生，教師可以進行猜想—驗證教學。

二、教學嘗試：讓學生在猜想—驗證中獲取數學思想

認知心理學派強調，學習中要學會質疑。教師要引導學生在探索中提出問題，從而加深對知識的理解，提高學習能力。為此，在教學中，教師應鼓勵學生大膽質疑。

（一）操作證偽：“難成平行四邊形”

浙教版六年級下冊數學《作業本》“圓柱的側面積“練習三第1題是這樣的：

有學生在解答時提出：圖②這條虛線這么直是不科學的。

教師追問：為什么這么說？

學生上臺邊演示邊說明：我們用軟三角尺貼住側面，假設這是那條線，您看，這條線畫在平面上不可能是直的，軟尺在曲面上，這條線必定有弧度。

（說明：三角尺太硬了，用長方形紙條來圍，它薄一點更能貼牢，這條邊的弧度更加明顯。）

生：如果非要做這道題，沿圖上的直直的虛線來剪，那我只能填近似的平行四邊形了。

這是一次課后練習中發生的小插曲，學生證偽成功，數學學習的自信瞬間提升。

（二）計算驗證：“格點法可用于多邊形面積計算”

學生一旦有了證明（驗證）的意識，思考問題的方式就會跟著發生改變。學生有了強烈的質疑和求證的意識，其日常的學習會變得很不一樣，思維就會慢慢走向高階。

如教學人教版五年級上冊第六單元“多邊形的面積”時，在完成基本教學任務的前提下，教師讓學生思考驗證“格點法是否可以解決多邊形面積計算”（格點多邊形面積=內格點數+邊格點數÷2-1）。學生帶著疑問開始學習。

學生小組合作，驗證過程如下：

經過驗證，小組討論得到結論：格點法可以解決多邊形面積計算的問題。（注：多邊形應為格點多邊形）

（三）圖解揭秘：“首同尾合十”的兩位數乘法巧算原理

乘法125×8可以巧算，還有一些也可以巧算。比如23×27，可以用“頭×（頭+1）”也就是20×30+“尾×尾”也就是3×7來計算等于621，這就是“首同尾合十”的兩位數乘兩位數的巧算。為什么呢？教師可以提供相應的學習材料讓學生操作思考。

[過程 舉例 形成觀點 模型

呈現立論 23×27=20×30+3×7=621 可以用“頭×（頭+1）”也就是2×3作積的前兩位，“尾×尾”作積的末兩位

驗證

嘗試應用 ①39×31=30×40+9×1=1209 √

②54×56=50×60+4×6=3024 √

③43×57=40×60+3×7=2421 ×

④27×26=20×30+6×7=642 ?× 計算發現①②的結果是正確的，③④的結果是錯誤的。說明并不是所有的兩位數乘兩位數都可以這樣來計算

探究

數形結合 ①39×31=30×40+9×1=1209

學生利用圖形，證明理解了巧算的原理，體驗了成功的喜悅，同時使觀察、質疑、推理、歸納、應用等高階思維能力得到了鍛煉。

三、數學教學要指向高階思維的培養：在猜想驗證中從“是什么”走向“為什么”

所謂高階思維，是指發生在較高認知水平層次上的心智活動或認知能力，主要指創新能力、問題求解能力、決策力和批判性思維能力。

對小學生來說，經歷歸納、猜想、證明（驗證）等過程是培養高階思維能力的有效舉措。教師授課不但要讓學生明白“是什么”，而且要讓他們明白“為什么”。

如人教版三年級下冊P65，P75分別有兩道練習題，一道是周長相等畫不同的長方形，另一道是面積相等畫不同的長方形。兩題均有讓學生思考的要求“你能發現什么”。這類練習課，教師都會直指規律，那就是“周長相等時，長與寬越接近，面積越大;面積相等時，長與寬越接近，周長越小”，讓學生初步感知這個規律。如果教學止步于此，學生腦海中留下的僅僅是問題的結論。教師不妨放手讓學生進一步探索證明“為什么會這樣”，引導學生的思維趨向高階。

教師出示改編后的學習材料供學生探索。

1.下面每個小正方形的邊長為1厘米。在方格紙上，畫出周長為24厘米的長方形，你能畫幾個？（1）獨立在方格紙上畫一畫。（2）小組合作，在記錄表中有序理一理。（3）思考：周長不變時，面積怎么變？為什么？

2.三（1）班要設計一面長方形笑臉墻，現有1平方分米的正方形照片20張，有多少種不同的擺法？如果給照片墻配上邊框，怎樣最節省材料，為什么？

教師引導學生在圖形對比、數據對比中層層深入，不斷挖掘知識的內涵，讓學生不斷經歷變與不變的歸納推理證明（驗證）過程，促進學生高階思維能力的提升。

參考文獻：

[1]吳衛東，林碧珍，章勤瓊.變學科邏輯為教學邏輯：臺灣“素養導向臆測教學模式”的教育學審視[J].教育發展研究，2018，38（20）：62-67.

[2]林琳，沈書生，李藝.談設計思維發展高階思維何以可能——基于皮亞杰發生認識論的視角[J].電化教育研究，2019（8）：1-8.

[3]李紅霞，崔靜靜.數學證明教學的思考[J].內江師范學院學報，2018，33（4）：38-41.

[4]張奠宙.從“三大能力”到“六大能力”[J].數學教學，2018（4）：50.

（浙江省杭州市青藍小學 ? 310003）