高中數學建模能力培養研究

摘 要：數學建模是數學核心素養的重要組成部分，通過模型的建立能夠讓學生充分理解所學的數學知識，通過規律的推導和總結，將數學知識通過數學語言表述以解決同類問題。但是建模過程耗時費力，很多教師都弱化這個能力培養，實際建模是能夠有效促進學生學習數學，應用數學的最佳途徑。本文通過高中數學建模教學案例分析，論述高中數學建模能力培養方法。

關鍵詞：高中數學，建模，教學，能力，核心素養

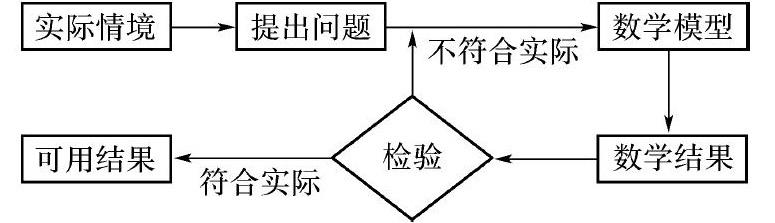
數學建模是數學六大核心素養之一，平時教學中數學建模能力的培養有助于高考中迅速解決數學問題。“數學建模”起源于數學邏輯推理能力和數學抽象概括能力基礎上進行想象、運算，最后用數學語言總結而成的一種數學模型。數學建模的流程如下：

一、 數學教學中培養數學建模能力的意義

著名數學家R·柯朗對于數學學習中只注重反反復復的習題訓練方法提出質疑，因為大量數學習題訓練只能提升解題能力，但是卻弱化了學生獨立思維能力，也忽視了數學的實際應用價值以及和其他學科的關聯。題海訓練讓學生只是被動地從作業中學習一些解題技巧，容易引起厭倦和反感。有過一個實驗，一所重點大學，學生入學成績數學平均120分，開學后，學校再次用高考難度的數學卷子考試，學生平均分卻下降到95分，再過一段時間，學校再次測驗，平均分都90分以下了，都沒有達到及格線。這是因為高考結束后，沒有高考壓力，很多知識和解題技巧都忘記了，說明都是為了高考有些知識是被動記憶而已，并沒有形成一種解決題能力。數學建模（mathematica modeling）是一種能力培養，一旦養成，就會長期運用并解決數學問題，讓學生體會到學習數學的意義和用處。

（一）有利于拓展學生知識面

數學建模并非易事，建模不僅僅只需要數學基礎知識，還需要了解其他學科的原理，一些數學模型建立需要調查研究實際情況，并查閱相關的資料，會涉及化學知識、經濟學原理、社會學問題等等學科范圍。所以建模過程學生也會拓展知識面，了解和學習其他專業知識。

（二）有利于增強學生的自學能力和創新能力

高考模式下很多只為分數的教學模式，老師做范例，學生模仿解題的教學模式不利于學生創新思維。隨著社會不斷進步，尤其我國的各行業快速發展，我們需要更多創新型人才，沒有自學能力和創新能力將來很難立足，我們既然培養人才，就要培養適應社會需求的人才。建模過程就是一種獨立思考和創新的過程，因為不是現成的模型去模仿，而是要求學生建立新的數學模型，學生必須經過思考、研究、計算、總結出別人沒有總結過的新模型。

（三）有利于培養學生集體合作能力

復雜的數學建模一般個人難以完成，需要多人合作，組成團隊，小組內一般會有明確的分工合作，研究過程中需要交流，還需要一個領導負責總體的研究事宜。這個過程中也能鍛煉學生的合作能力，集思廣益、取長補短，這對將來個人的發展有更重要的意義。

（四）有助于提高學生的綜合素養

高中的數學建模范圍很廣，各個模塊都可以建模，比如函數、不等式、立體幾何、概率、向量等等都可以進行建模。數學建模是基于數學抽象能力和想象力以及計算和推理能力，建模過程也是反復推理運算的過程，因此，開展數學建模教學對于學生的綜合素養和能力都有巨大的幫助作用。

二、 例談如何培養學生數學建模能力

數學建模的目標就是用于解決實際生活中的問題，高中生已經能夠觀察生活，發現問題，進行思考，如果能夠建模去解決，那么就達到了學以致用。所以很多建模的出發點都是聯系生活實際，并且有推廣價值的。

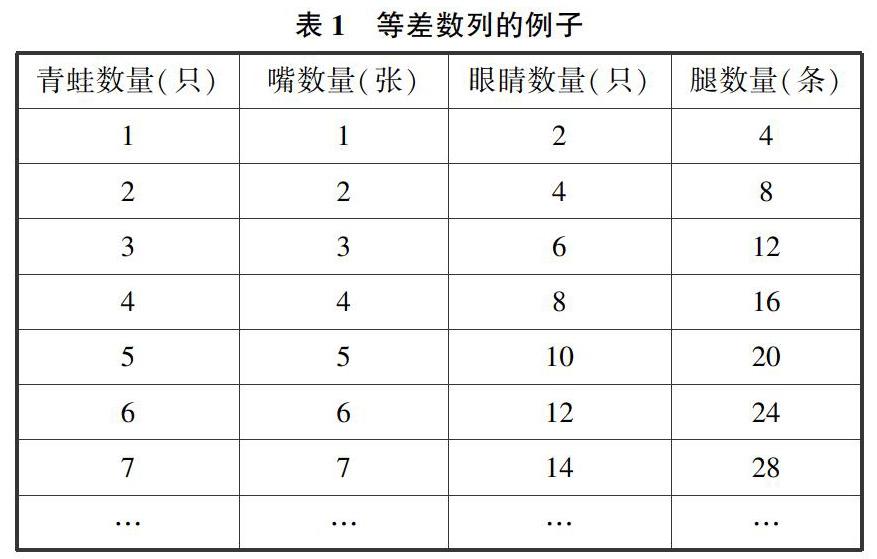
比如課上學習等差數列課程的時候，可以先播放一段童謠：“一只青蛙，一張嘴，兩只眼睛，四條腿，兩只青蛙，兩張嘴，四只眼睛，八條腿，三只青蛙，三張嘴，六只眼睛，十二條腿。”然后讓同學們先列表找規律，列表如表1所示。

在童謠聲中，同學們能夠很快對數列產生濃厚的興趣并且進行分析思考，列表之后學生很快能夠按照各列數據發現等差的規律，從而對等差數列的概念產生深刻的印象，通過簡單的例子能夠讓學生為模型的建立打下一定的基礎。

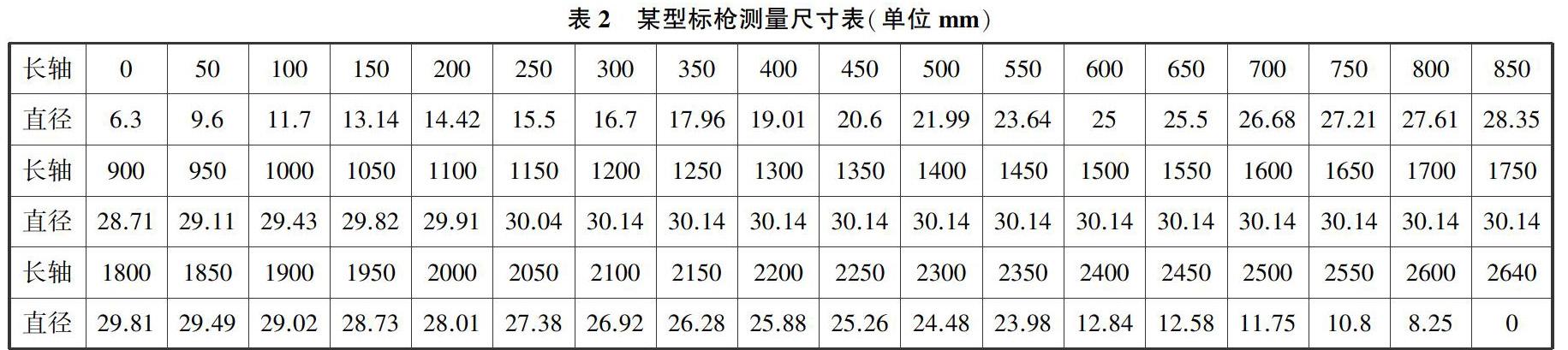
再如運動賽場的標槍投擲項目，這是常見的田徑賽事，國家有標準的標槍分類和各項指標參數，表2是某型比賽標槍的測量尺寸數據，那么可以讓同學們根據表格參數去估算標槍標槍沿標槍中軸線剖面面積、標槍表面積和標槍形心的位置，其中形心是指標槍沿中軸線剖面圖形的幾何中心。

診斷分析：根據該國家標準中的標槍示意圖，我們相信學生對中軸線剖面和表面的理解是明確的。這兩個面的面積可以用下面兩種方法求得。我們可以依據尺寸表將標槍分成若干小段，每一小段的剖面和表面就可以分別近似成一個梯形和一個圓臺的側面，因此可以用初等數學的方法通過累加得到剖面面積和表面積的近似值。更準確一點的，我們可以將標槍放至坐標系中，借助于Matlab擬合工具箱對尺寸數據進行擬合處理，將標槍剖面輪廓用多項式函數曲線去近似，然后利用函數積分計算得到剖面面積和表面積。課標中雖然有幾何對象、位置關系等內容，但對于形心并無明確說明，在尋找標槍形心位置之前，我們需要準確理解形心的概念，最好能夠理解物體的形心、質心和重心之間的聯系和區別。由于尺寸表給出的是長軸上某位置的直徑，我們可以假設標槍的截面是圓面，這樣標槍的形心一定位于中軸線上。對于形心位置的確定，我們也可以借鑒上述兩種處理方法，借助于梯形、離散點的形心公式和Matlab求形心方法類似得到。

三、 總結

總而言之，數學建模有助于數學核心素養的培養，有利于學生拓寬視野，有助于綜合能力的培養，還能夠培養合作精神和探索創新能力。數學建模能力的培養需要數學教學工作者將實際生活中的問題與學習相關知識相互聯系，設置題境，引導學生去思考，計算、推理，最后總結出公式，最后能夠解決問題。

參考文獻：

[1]李永聲.注重培養數學建模能力 提升數學核心素養[J].中學教學參考，2019（26）.

[2]林品玲.核心素養下數學建模能力的培養[J].當代家庭教育，2019（23）.

[3]陳炳泉.高中數學核心素養之數學建模能力培養的研究[J].當代教研論叢，2018（11）.

[4]張武梅.核心素養下初中數學建模能力的培養[J].數學學習與研究，2019（14）.

[5]徐斌艷，沈丹.我國學生的數學建模能力水平分析：以6～9年級學生的“縫制足球”實驗為例[J].中學數學月刊，2014（7）.

[6]錢景.淺談中專學生數學建模能力的培養與探索[J].課程教育研究，2014（36）.

[7]楊靜.國外高中生數學建模能力評價研究綜述[J].數學教學，2017（9）.

[8]陳維強.初中數學建模能力缺失分析及培養對策[J].課程教育研究，2017（31）.

[9]韓建.小議初中生數學建模能力缺失的因素與培養對策[J].中學數學，2017（18）.

[10]劉大本.淺談學生數學建模能力的培養[J].江西教育，2006（22）.

[11]李大潛.數學建模的教育是數學與工業間最重要的教育界面[J].數學建模及其應用，2012，1（1）：38-41.

[12]中華人民共和國教育部.普通高中數學課程標準（2017年版）[S].北京：人民教育出版社，2018.

[13]李明振，喻平.高中數學建模課程實施的背景、問題與對策[J].數學通報，2008，47（11）：8-10.

[14]張思明.中學數學建模與探究[M].北京：高等教育出版社，2018.

[15]劉鳳秋，畢卉，陳東彥，李冬梅，孫偉.融合數學建模思想的理工科研究生創新能力培養模式[J].高師理科學刊，2014（5）.

作者簡介：

羅志華，福建省三明市，福建省建寧縣第一中學。