指向思維可視化的數學概念教學

【摘? ?要】指向思維可視化的數學教學是指借助圖示、動作、文字、符號等多種數學語言相互轉化的視覺學習，將看不見的思維路徑顯性化，有利于學生的學和教師的教。概念教學中的可視化圖示工具可從前結構、單點結構、多點結構和關聯結構這四個層級來建構。指向思維可視化的概念教學，可從“原型重現”“初建表象”“表征內化”“結構完善”四方面展開。

【關鍵詞】思維可視化;小學數學;概念教學

思維可視化是指將看不見的思維路徑顯性化，通常借助圖示、動作、文字、符號等來實現。它不僅是一種教學理念，更是一種教學行動，通過引導學生經歷“直觀地看”“形象地畫”“出聲地想”等過程，達到思維可視化的目的。

一、思維可視化在概念教學中的作用

數學概念是數學的重要基石，教學中教師要基于學科本質，借助“情境→直觀→操作”，引導學生理解數學概念，經歷概念形成與同化的過程，把握概念的本質意義。在這一過程中，思維可視化的作用主要體現在以下幾方面。

（一）使概念具象化

數學概念教學需要還原生成概念的全過程，即意義建構的過程，但學生在理解概念的過程中往往會出現思維斷層的現象。指向思維可視化的概念教學，能幫助學生跨越思維斷層，促進概念意義的理解。例如，分數是一個抽象的概念，三年級學生要去理解它并不容易，教學時需要為學生提供直觀模型，為學生提供看得見、摸得著的思維支架，把抽象的分數和具體的圖像聯系起來，促使分數概念具象化，幫助學生理解分數概念。

（二）促知識結構化

借助思維可視化，可以使“點狀”的單個概念走向“網狀”的概念結構。例如，周長與面積學生容易混淆。教師可以借助對“邊長是4分米的正方形，面積與周長相等”的辨析展開教學，引導學生通過在格子圖中畫一畫、列表比一比等可視化操作活動，發(fā)現周長與面積的聯系和區(qū)別，形成較為完善的知識結構。

（三）讓經驗模型化

“四基”是新一輪教學改革的要求，數學基本活動經驗是“四基”的一個維度。思維可視化不僅在數學知識結構化上會產生一定的作用，在數學活動經驗模型化上也有著積極的意義。例如在面積的教學中，教師通常會引導學生經歷從定性到定量的認識過程，讓學生對“度量”的三要素有整體把握，建構起“度量”經驗的模型。

二、概念教學中思維可視化的可用工具

曹培英認為，根據可觀察的學習結果（SOLO分類評價法），可以將數學理解層次進行梯狀刻畫，分別是前結構水平、單點結構水平、多點結構水平、關聯結構水平和拓展抽象水平。基于數學理解的這五個水平層次，筆者認為概念教學中的可視化圖示工具可以從前結構、單點結構、多點結構和關聯結構這四個層級來建構，分別表現為實物圖、直觀模型、表格、韋恩圖、思維導圖、概念地圖、思維樹等。

（一）前結構的圖示工具，喚醒經驗

前結構的圖示，基于學生的生活經驗，與現實情境緊密結合，通常表現為生活場景或實物圖。例如學生在學習周長概念時已經有一些模糊的前概念，已經接觸到大量的周長情境，如體育課沿著操場跑一圈、美術課的剪紙、生活中鐘面上指針的走動，等等。教學時，教師可采用這些現實情境的動態(tài)演示，喚醒學生的生活經驗，初步建立“一周表象”。

（二）單點結構的圖示工具，聚焦本質

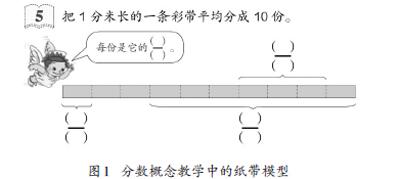
單點結構的圖示，指向概念的本質屬性。比如，直觀模型是分數教學中重要的可視化思維工具，可以是面積模型，也可以采用線段模型、集合模型等。一般來說，這些圖示的結構簡單，主要聚焦核心要素“平均分”。在認識十分之幾的分數時，就可以以這條1分米長的紙帶作為學習工具（見圖1），從“部分—整體”關系的角度來認識十分之幾。

（三）多點結構的圖示工具，厘清關系

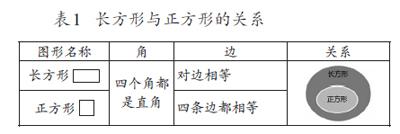
多點結構的圖示，重在溝通知識間的聯系，并在知識的生長點上作重點刻畫，幫助學生厘清知識之間的內在聯系，通常以列表、韋恩圖等形式表現。例如在四邊形的認識中，教師引導學生對一組圖形進行分類，讓學生通過比較和分類，歸納并概括出四邊形的類型，并聚焦到長方形和正方形的再認識上來，通過列表的可視方法凸現“角”“邊”的特征，再用韋恩圖表征兩者的關系（見表1）。

（四）關聯結構的圖示工具，建構體系

關聯結構的圖示，重在表現知識鏈與思維鏈縱橫交錯的結構。思維導圖、概念地圖、思維樹等就屬于這一層級的可視化工具。例如在概念教學中，教師可用節(jié)點表示概念，連線表示概念之間的關系，通過提綱式、輻射式、發(fā)散式等不同思維路徑反映概念之間的層級關系，建構知識體系。

三、指向思維可視化的概念教學結構

指向思維可視化的概念教學，可經歷“原型重現→初建表象→表征內化→結構完善”的過程，達到概念建構的目的。

（一）“原型”搭橋，對接生活經驗

概念教學的起始階段，思維可視作用主要體現在與生活經驗對接上，以“直觀地看”為主要活動形式。一般在課堂上，教師會采用前結構的圖示，即用生活中的原型來引入。現實生活中的原型（前概念）是理解概念不可或缺的學習素材。例如，分數的原型之一是“平均分物”，教學中用“分蛋糕”作原型，經歷以下學習過程。

1.出示情境圖，喚醒生活經驗：4個蛋糕平均分給2個人，每個人分到幾個？2個蛋糕呢？1個蛋糕呢？你能用合適的數分別表示平均分的結果嗎？

2.動態(tài)直觀演示，初步感悟分數：結合對1個蛋糕平均分的動畫演示，理解“半個→[12]個”“[13]個”“[14]個”是多大。

在這里，教師像引入自然數一樣引入分數，借助平均分的生活原型，喚醒學生的生活經驗。為讓學生初步認識分數，積累等分經驗，教師引導學生參與創(chuàng)造[12]，利用[12]個、[13]個、[14]個的實物模型，讓學生知道分數的意義，在具體“平均分”的可視化情境中初步建立分數概念。

（二）“表象”支撐，對接心理圖示

在初識概念后，概念會以一定的表象在學生的頭腦中編碼儲存，從而產生心理圖示。這時候，教師就要提供呈單點結構或多點結構的可視化圖示，引導學生經歷“直觀地想”“形象地畫”等可視化學習過程，促成概念表象的具象化。例如“1厘米”表象的建立，教師就可借助尺子這一可視化學習工具，采用以下幾個步驟組織教學。

1.尺子上的1厘米：這把尺子中隱藏著許多1厘米，請你在尺子上找一個你心中的1厘米。

2.生活中的1厘米：哪些物體的長度或厚度大約是1厘米？

3.頭腦中的1厘米：閉眼想象、用手比畫1厘米有多長，再徒手畫一畫。

通過找、想、比、畫等可視化的方式，物化學生頭腦中的1厘米，轉化成學生可觸摸的指甲長度、書本厚度等生活參照物，化抽象為具體，幫助學生建立起1厘米的表象。

（三）“表征”操作，對接概念內涵

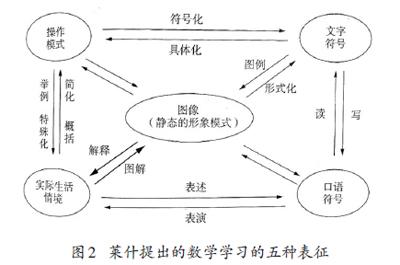
萊什提出數學學習的五種表征（見圖2），分別為實際生活情境、圖像、操作模式、口語符號和文字符號。當學生對概念表象具象化時，教學應借助這五種表征活動讓概念表象操作化與活動化，實現多種表征之間的溝通互譯，促進概念的深化理解，這是概念教學精致化的過程。

例如認識幾分之幾的教學，學生雖然有幾分之一的概念，但認知經驗和活動經驗還顯得比較單薄，教學中依然需要通過折一折、畫一畫、說一說、辯一辯等多元表征活動，讓學生借助四等分的正方形創(chuàng)造四分之幾，在動手操作中感受四分之幾的含義。活動后，組織學生匯報，并針對學生可能出現的情況，教師追問梳理，分4個層次。

追問1：這些分數里面各有幾個[14]？

學生對于[44的]理解可能會有困難，教師可以結合圖示以及其與[14]的聯系來讓學生理解[44]。

追問2：為什么涂色部分的形狀不一樣，卻都可以用[34]來表示？

追問3：你知道下面圖形中涂色部分是整個圖形的[□□]嗎？（長方形、圓、三角形、線段）

追問4：在下面的巧克力圖中，你能找到哪些分數（平均分成2份;平均分成4份;平均分成8份）？與同桌一起找一找，并說一說每個分數表示什么。

在這一過程中，教學所采用的圖示思維工具一般是多點結構的，教學經歷動手操作、畫圖說明、語言表達、生活拓展等思維活動，與分數建立互譯溝通，幫助學生理解分數概念。

（四）“結構”完善，對接概念體系

在概念深化理解的過程中，需要對學生的認知結構進行改組與擴充，形成概念網。例如學完“比”后，需要對“除法”“分數”“比”這三者之間的關系進行梳理，可通過列表（見表2）厘清概念之間的內在聯系與區(qū)別，完善認知結構。

綜上所述，利用可視化工具，讓學生在概念的產生、形成、理解、深化的過程中，實現概念的意義建構、概念體系的建構。

指向思維可視化的概念教學意味著教學研究的視角亦要革新。在課前，教師需要深度解讀概念的本質，明了思維可視化在本課教學的落腳點;需要深度理解學生，把握學生的前概念水平;需要深度解讀教材，明晰可視化思維的支架有哪些及如何用好這些支架;需要深度設計教學，把握指向思維可視化的教學路徑。

參考文獻：

[1]蔣碧云.基于“數學理解層次”的教學路徑探索——思維可視化的另一種打開方式[J].上海教育科研，2019（22）：68-71.

[2]葛素兒.思維可視，情理相融——第一學段數學教學中圖式思維活動的設計與運用[J].教學月刊·小學版（數學），2015（10）：40-42.

[3]尹晗，張際平.思維可視化視角下的未來課堂架構研究[J].遠程教育雜志，2016（2）：106-112.

[4]席愛勇.數學多元表征：讓概念形成過程“看得見”[J].教育研究與評論（小學教育教學版），2017（9）：65-67.

（浙江省杭州市富陽區(qū)富春第二小學? ?311400）