數(shù)學(xué)課堂問題情境引入設(shè)計的五個著力點

摘? ?要 數(shù)學(xué)課堂引入應(yīng)關(guān)注從學(xué)科角度創(chuàng)設(shè)問題情境，著力于知識之間聯(lián)系的“聯(lián)結(jié)點”，知識形成發(fā)展過程的“關(guān)鍵點”，問題解決策略產(chǎn)生過程的“關(guān)節(jié)點”，知識背景、抽象歸納過程的“本原點”和知識變形、運算、推理過程的“發(fā)散點”，從而最大限度地促進(jìn)有效教學(xué)的發(fā)生。

關(guān)鍵詞 數(shù)學(xué)課堂? 學(xué)科情境 著力點

課堂引入是教學(xué)的正式啟動，是教學(xué)的重要一環(huán)。新課改以來，通過創(chuàng)設(shè)現(xiàn)實問題情境引入新課是一種較為常見的方法，而少有從學(xué)科知識角度思考課堂引入的方法和意義。馬克思說：“形式應(yīng)是內(nèi)容的形式，否則，它就失去了價值。”課堂引入設(shè)計時，教師首先要明確，形式始終要服務(wù)于內(nèi)容。如果過于強(qiáng)調(diào)引入的表面形式和非認(rèn)知因素作用，常常會削弱或脫離學(xué)科知識的本質(zhì)，看似引起了注意，調(diào)動了興趣，激發(fā)了動機(jī)，實則弱化了課堂引入的認(rèn)知因素作用，并不利于知識的意義建構(gòu)。項武義教授曾指出：目前的數(shù)學(xué)教育存在著“去數(shù)學(xué)化”的傾向，看重教育心理學(xué)規(guī)律，忽視了對數(shù)學(xué)本質(zhì)的揭露，尤其是在課堂引入環(huán)節(jié)。單墫教授也認(rèn)為：數(shù)學(xué)課就是講數(shù)學(xué)的，是解決數(shù)學(xué)問題而非實際問題，有些數(shù)學(xué)課，片面聯(lián)系實際，是舍本求末。

在數(shù)學(xué)課堂的引入設(shè)計中，如何從學(xué)科角度發(fā)現(xiàn)和提出值得研究的問題，值得引起每一位數(shù)學(xué)同行的高度關(guān)注。筆者以為，用心捕捉并著力于知識內(nèi)容在發(fā)生、發(fā)展過程中起關(guān)鍵作用的“核心點”，可最大限度地促進(jìn)有效教學(xué)的發(fā)生。

一、著力于知識間聯(lián)系的“聯(lián)結(jié)點”

數(shù)學(xué)的主要特點是其邏輯的嚴(yán)謹(jǐn)性，而思想方法的一致連貫性和不同知識的聯(lián)系性則是嚴(yán)謹(jǐn)性的關(guān)鍵。課堂引入時，著力于知識間的內(nèi)在聯(lián)系，使其相互溝通，不僅是建立數(shù)學(xué)良好認(rèn)知結(jié)構(gòu)的需要，也是提高學(xué)生數(shù)學(xué)整體認(rèn)識水平的需要。

如教學(xué)“三角形中位線定理”時，若僅從這個單一知識點的學(xué)習(xí)來看，通過設(shè)計測量等方面的現(xiàn)實問題情境，激發(fā)學(xué)習(xí)動機(jī)，也是無可厚非的。但若從前后知識間的關(guān)聯(lián)、從系統(tǒng)和整體的角度分析，這種做法就不夠全面。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)》把本節(jié)內(nèi)容放在了四邊形的框架下，表明了編者“運用平行四邊形知識探究本節(jié)內(nèi)容”的意圖，而且這一意圖也在不同版本的教材上得到了很好的體現(xiàn)。因此，從這個角度出發(fā)，本課的引入設(shè)計思路應(yīng)順著平行四邊形性質(zhì)的探究，讓學(xué)生自然而然地發(fā)現(xiàn)并提出定理，而非創(chuàng)設(shè)新的現(xiàn)實問題情境。

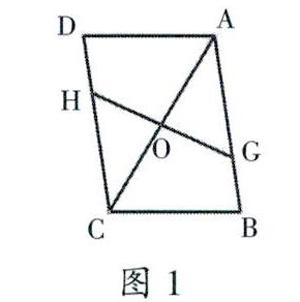
例1.利用平行四邊形的性質(zhì)，你能探索下面的問題嗎？

（1）如圖1，GH是過？荀ABCD對角線AC中點O的一條直線，分別交AB、CD于點G、H，請判斷AC與GH的關(guān)系，并給出你的證明。

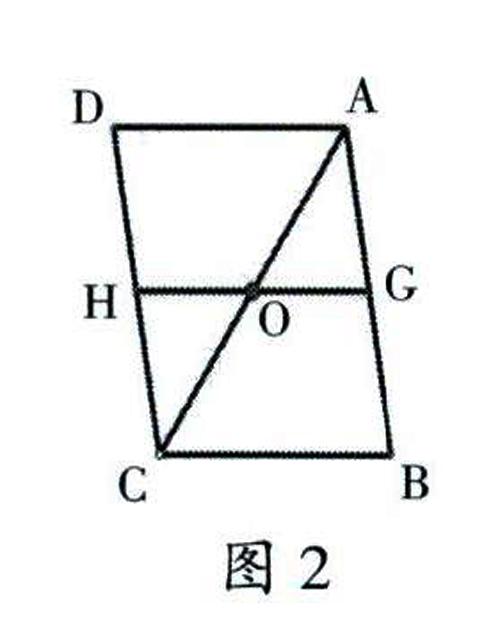
（2）如圖2，若點G為邊AB的中點，請判斷GH與BC的關(guān)系，并給出你的證明。

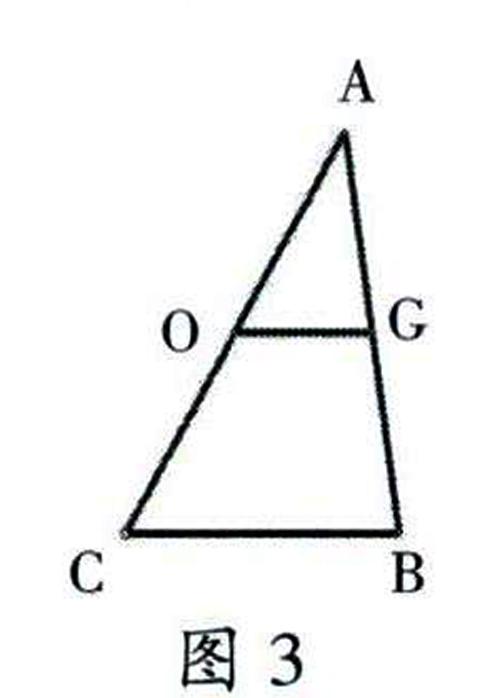
（3）在圖3的△ABC中，O、G分別是兩邊AC、AB的中點。我們把連接一個三角形兩邊中點的線段叫三角形的中位線。你能探究三角形的中位線有什么性質(zhì)嗎？

顯然，這種設(shè)計不僅使定理的提出與發(fā)現(xiàn)自然合理，也為學(xué)生證明定理提供了思路：通過截取或延長把線段倍分且平行問題轉(zhuǎn)化為線段之間的相等且平行問題。這對研究幾何圖形一般套路的靈活運用、發(fā)展學(xué)生的數(shù)學(xué)探究能力和思考活動的經(jīng)驗都極為有利。

二、著力于知識形成發(fā)展過程的“關(guān)鍵點”

隨著學(xué)習(xí)的逐步深入、內(nèi)容抽象程度的逐漸提高，中學(xué)數(shù)學(xué)的許多知識，在課堂引入時，更應(yīng)強(qiáng)調(diào)從知識形成發(fā)展過程的邏輯必然中提出問題。

如在“圓與圓位置關(guān)系”教學(xué)中，由于學(xué)生對圓的接觸較早，對圓的感性認(rèn)識已較為豐富，加之學(xué)生通過對圓的相關(guān)性質(zhì)和與圓有關(guān)的兩種位置關(guān)系的研究學(xué)習(xí)，對圓的理性認(rèn)識也已具備較高水平。特別是圓與圓和點與圓、直線與圓的位置關(guān)系不僅“同質(zhì)”，而且對其研究的方法也“一脈相通”，只是復(fù)雜程度相對較高而已。因此，本課引入的起點，不應(yīng)再是奧運五環(huán)、汽車車輪等“生活的”現(xiàn)實，而應(yīng)是“數(shù)學(xué)的”現(xiàn)實。

例2.設(shè)計如下問題：

（1）在與圓有關(guān)的位置關(guān)系中，你認(rèn)為還可以研究什么？

（2）你能回憶一下我們是如何研究前兩種位置關(guān)系的嗎？

（3）類比前兩種位置關(guān)系的研究方法和過程，你認(rèn)為可以怎樣研究圓與圓的位置關(guān)系呢？

顯然，這種設(shè)計邏輯連貫、至精至簡，它專注于知識的形成發(fā)展過程，強(qiáng)調(diào)思考、解決問題的返璞歸真，強(qiáng)調(diào)數(shù)學(xué)思考方法真諦的領(lǐng)悟。

三、著力于問題解決策略產(chǎn)生過程的“關(guān)節(jié)點”

策略性知識與數(shù)學(xué)具體知識是相互融合的，只要教師能有意識地滲透，學(xué)生就可獲得相關(guān)問題的解決策略。課堂引入時，結(jié)合具體的內(nèi)容，通過創(chuàng)設(shè)恰當(dāng)、適度的問題情境，加強(qiáng)類比、歸納、抽象等思維方法的引導(dǎo)，使策略性知識和具體數(shù)學(xué)知識的學(xué)習(xí)和運用有機(jī)結(jié)合起來。

如在教學(xué)“梯形面積公式”時，若在設(shè)計時能多考慮些問題解決策略和思想方法的啟發(fā)與引導(dǎo)，則會收到更好的效果。

例3.（1）你能回憶一下我們是怎樣利用矩形面積得出平行四邊形面積的嗎？三角形的面積呢？

（2）類似地，你能利用已有的面積公式得出梯形的面積公式嗎？

顯然，這種設(shè)計引導(dǎo)學(xué)生自己得出解決問題的策略——轉(zhuǎn)化為平行四邊形面積問題。突出了知識間的結(jié)構(gòu)與聯(lián)系，為學(xué)生的獨立思考提供了較為充分的空間，又是學(xué)生“跳一跳、夠得著”的。

四、著力于知識背景、抽象歸納過程的“本原點”

華羅庚說過：遇到一個復(fù)雜問題，足夠地“退”，退到能想透、想通的最本原、最簡單的問題，然后再歸納、抽象而實現(xiàn)突破，是學(xué)好數(shù)學(xué)的一個“竅門”。在日常的教學(xué)中，常可發(fā)現(xiàn)由于教師對所學(xué)知識的背景、抽象歸納的過程缺乏深入的“本原”性分析，致使課堂上沒有貫穿始終的教學(xué)主線，缺乏能開啟學(xué)生思維的問題引領(lǐng)，教學(xué)的過程隨意，給了學(xué)生一筆“糊涂賬”。

如“二項式定理”作為數(shù)學(xué)內(nèi)部推理的結(jié)論，對這個公式的推導(dǎo)，追本溯源就是多項式乘法問題，因此，多項式的乘法法則是公式推導(dǎo)的“本原點”。又因其因式都相同的特殊性，決定了其展開式的規(guī)律性，在探索這個規(guī)律的過程中所用到的組合數(shù)知識則是公式推導(dǎo)的輔助“本原”。本課的引入設(shè)計就是要從“還原”這個既有歸納、抽象又有演繹的過程入手，在“本原點”處提出適切的問題，引導(dǎo)學(xué)生的探究活動。

例4.（1）你能從（a+b）2=a2+2ab+b2出發(fā)，得到（a+b）3、（a+b）4的展開式嗎？

（2）你認(rèn)為應(yīng)從哪幾個方面觀察上式的共同結(jié)構(gòu)特征呢？由此你能得出（a+b）n展開式的哪些猜想？

（3）既然用上述遞推方法難以得出展開式各項系數(shù)，你能換個角度思考這個問題嗎？

這種設(shè)計引導(dǎo)學(xué)生回歸本原，觀察、思考多項式“要素”的規(guī)律，特別是各項的次數(shù)及a、b次數(shù)的變化規(guī)律;再通過歸納、抽象，利用組合數(shù)公式表示系數(shù)，進(jìn)而得出一般結(jié)論，這也正是“玩概念”的含義。

顯然，這種基于學(xué)生已有知識經(jīng)驗的“本原”性引入設(shè)計，構(gòu)建了清晰、連貫的教學(xué)主線，結(jié)合課堂中的動態(tài)生成予以展開，讓學(xué)生經(jīng)歷定理的探究過程，真正實現(xiàn)二項式定理的數(shù)學(xué)育人價值。

五、著力于知識變形、運算、推理過程的“發(fā)散點”

當(dāng)新知識是對已有公式、概念的精確化、具體化，這時的新知學(xué)習(xí)稱為下位學(xué)習(xí)。引入新課時，常可在原有知識基礎(chǔ)上，通過適當(dāng)?shù)淖冃巍⑦\算和推理提出學(xué)生利用已有知識難以正確回答的問題，讓學(xué)生在錯誤中感觸矛盾的沖突，生成問題情境，激起學(xué)生內(nèi)在的學(xué)習(xí)動機(jī)。

如在教學(xué)“=|a|”時，一位教師在回顧（）2=a后，便開門見山，直奔主題：若把此式中的“平方記號”“移到”根號內(nèi)，那么①=？②=？由于學(xué)生剛剛學(xué)過（）2，其中a的范圍與原有的算術(shù)平方根概念一致，這個問題的提出擴(kuò)大了a的范圍，而學(xué)生的認(rèn)識又不能與之同步，大多會在符號上出現(xiàn)錯誤，這也正是教師情境設(shè)計的出發(fā)點。有不少學(xué)生認(rèn)為：=a，=-a，于是教師便抓住“時機(jī)”，“將錯就錯”：因為a2=（-a）2，應(yīng)有=，于是a=-a！即任何實數(shù)都與它的相反數(shù)相等，這是一個令學(xué)生驚訝的結(jié)論，激起了學(xué)生想“弄個明白”的學(xué)習(xí)沖動。在此基礎(chǔ)上，教師只需引導(dǎo)學(xué)生“由特殊到一般”，從具體數(shù)值的運算中進(jìn)行歸納、總結(jié)，再聯(lián)系絕對值的概念，通過對比即可獲得公式：=|a|=a（a>0）0（a=0）-a（a<0）? .

可見，這種從“數(shù)學(xué)”到“數(shù)學(xué)”地引入，同樣能使學(xué)生因“心動”而“行動”，讓學(xué)生從切身體驗中學(xué)習(xí)新知識，讓學(xué)習(xí)富有情趣。

巴班斯基說：無論是現(xiàn)在還是將來都不可能有最萬能、最有效的方法，本質(zhì)上來說每一種教學(xué)方法都是辯證的，能很好完成某些任務(wù)、達(dá)到某些特定目的，但不能完成所有任務(wù)、達(dá)到所有目的。課堂引入也是如此，“引入有法”但“引無定法”，引入方法的不同其所發(fā)揮的作用就存有差異，它們相輔相成，又相得益彰。因此，強(qiáng)調(diào)學(xué)科問題情境引入設(shè)計，并非完全否定實際問題情境，只有根據(jù)知識內(nèi)容靈活選取或有效融合，才能收到好的效果。

參考文獻(xiàn)

[1] 章建躍.章建躍數(shù)學(xué)教育隨想錄下卷[M].杭州：浙江教育出版社，2017.

[2] 田蕓.問題情境創(chuàng)設(shè)應(yīng)規(guī)避的幾個問題[J].教學(xué)與管理，2016（17）.

[3] 李祎.另眼看導(dǎo)入[J].數(shù)學(xué)通報，2018（08）.

[4] 戴文革.品讀“情境引入”問題設(shè)計的“數(shù)學(xué)味”[J].中學(xué)數(shù)學(xué)教學(xué)參考，2017（05）.

[5] 章建躍.構(gòu)造邏輯連貫的學(xué)習(xí)過程使學(xué)生學(xué)會思考[J].數(shù)學(xué)通報，2013（06）.

[6] 程新展.還課堂一個自然的過程[J].中學(xué)數(shù)學(xué)月刊，2008（08）.

【責(zé)任編輯? ?郭振玲】

該文為江蘇省教育科學(xué)十二五規(guī)劃課題“初中‘選學(xué)走組制教學(xué)的實踐研究”（B-b/2015/02/240）的階段性成果