整體關聯，促進學生建構知識

翟瑩

[摘 要]數學教學中，教師可從知識的整體關聯入手，引導學生不斷深入探究，使學生所學的數學知識形成一個有機的整體，實現從整體上提升學生數學核心素養的目的。

[關鍵詞]整體;關聯;建構;數學教學

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2020）21-0035-02

布魯納指出：“學習就是認知結構的組織與重新組織。”數學知識不是孤立存在的，而是相互關聯的。但是，在平時的數學教學中，教師常常注重各個知識點的教學，忽視了數學知識之間的整體關聯，不利于學生建構完整的知識體系。因此，教師應從學生已有的知識經驗出發，將教學內容置于整個數學知識體系中去設計教學，引導學生經歷知識發生、發展和形成的過程，使學生真正理解和掌握所學的數學知識，提升學生的數學學習效率。

一、注重數與數的關聯，整體內化

數是數學的重要內容。在數的認識教學中，教師要善于從知識的本質入手，找準數的概念之間的聯系，溝通數與數之間聯系的紐帶，然后連點成線，促進學生整體建構數的認知，真正內化所學的數學知識。

例如，以小數與整數教學為例，它們的本質都是十進制數，它們的計數單位之間存在著密切的聯系，即可以把它們看作由計數單位1向兩邊無限延伸演變而成。因此，教師可從小數的意義入手，幫助學生建立起小數與整數之間的關聯，使學生對數形成整體認識。課堂上，教師從認識1元、10元、100元的人民幣入手，引導學生按照1、10、100之間的進率進行換算，并以100格的正方形紙為例，讓學生說說分別是多少元。然后教師提出問題：“不滿1格怎么辦？”經過分析思考，學生得出結論：可以借助元、角、分的十進制關系，把整數之間相鄰兩個單位之間的進率定為十，這樣把1平均分成10份，每份就是0.1元;不足0.1元時，再把0.1元平均分成10份，那么每份就是0.01元。這樣將小數與整數結合起來進行教學，使學生體驗到整數是學習小數的基礎，實現數學知識的“再創造”。

數學教學中，教師要從整體上審視各個知識點，把握各個知識點的來龍去脈，幫助學生形成對所學知識的整體認知。數的范圍很廣，不僅包括整數和分數，還包括百分數等。因此，在數的認識教學中，教師要注重數與數之間的關聯性，使學生明白各種數之間的聯系，從而結點成網，形成關于數的認識的結構網絡。

二、注重數與例的關聯，整體貫通

“數學源于生活，用于生活，高于生活。”因此，教師要善于把教學內容置于學生熟悉的實際生活中，使其成為學生學習數學的內驅力。數學課堂中，教師可引導學生從整體上溝通知識之間的內在聯系，實現學生數學認知的整體建構。

例如，教學《速度、時間和路程》時，學生通過字面意思對時間與路程有一定的了解，而對于速度，多數學生的認知停留在快慢的層面上。那么，怎樣才能促進學生對問題的整體認知呢？首先，教師為學生創設具體的教學情境，引導學生比快慢：“假如小芳家到學校是240米，她用了5分鐘走到學校;小明家到學校是250米，他用了5分鐘走到學校。你知道他倆誰走得快嗎？”這里，由于路程不同，“誰走得快”就是衡量速度的一個標準，教師這樣教學水到渠成。其次，教師設計習題，讓學生進行求速度的訓練。在此基礎上，教師引導學生總結出路程、速度、時間之間的數量關系。這樣教學，使學生對路程、速度、時間之間數量關系的認識更加系統化，豐富了學生的數學認知。

數學教學中，教師通過創設問題情境，引導學生經歷“引出模型——抽象模型——豐富模型”的思維過程，幫助學生獲得對數學知識的本質認識，使學生形成對所學知識的整體建構。同時，這樣教學有助于學生觸類旁通、舉一反三，積累更多的數學活動經驗。

三、注重數與形的關聯，整體重構

著名數學家華羅庚曾說過：“數缺形時少直觀，形少數時難入微;數形結合百般好，隔離分家萬事休。”因此，數學教學中，教師要注重數與形之間的關聯，從數學知識整體的角度，深化學生對所學數學知識的理解，實現優化數學教學的目的。

例如，計算破碎鐘面的周長，有的學生說“這道題沒法計算，要把鐘面還原后才能求出它的周長”;有的學生說“要知道這個鐘面的半徑，才能計算出它的周長”。學生的思維陷于困境，于是教師提問：“怎樣才能求出這個鐘面的周長呢？能不能用類推的方法來解決呢？”在教師的啟發下，學生想到可以先量出鐘面的一大格，再把它乘以12（鐘面有12個大格，每個大格的長度都相等）就可以得出鐘面的周長了。這樣看形思數、以數助形，幫助學生溝通了鐘面大格、份數之間的關聯，使學生形成鐘面知識的整體建構。

數學教學中，教師應幫助學生形成對所學知識的整體認知，啟發學生變換角度思考問題，這樣有助于學生突破思維定式，將習得的數學知識融會貫通、重新建構，提高數學課堂教學效率。

四、注重數與法的關聯，整體建構

數學思想方法是對數學知識、方法、規律的本質認識，是數學思維的結晶和概括，是解決數學問題的靈魂和根本策略。因此，數學教學中，教師要注重數學思想方法的滲透，使學生真正理解和掌握所學的數學知識，提升數學學習能力。

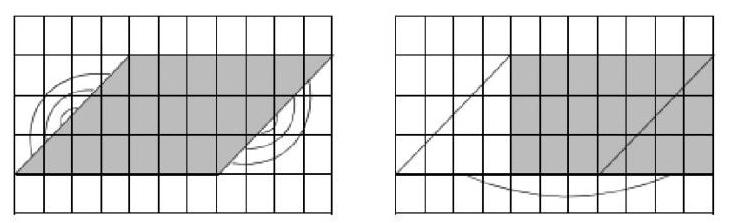
例如，教學《平行四邊形的面積》一課時，這部分內容不僅是小學平面圖形的重要內容，而且是“圖形與幾何”領域承上啟下的內容，對學生今后學習平面圖形有著重要的作用。那么，教師在教學中如何幫助學生積累數學活動經驗，滲透數學思想方法呢？課始，教師通過數一數、剪一剪等活動，幫助學生積累轉化的經驗，使學生明白僅用數方格的方法來探究平行四邊形的面積是不夠的。然后教師通過多媒體呈現圖示（如下），讓學生思考為什么要沿著高展開探究平行四邊形的面積計算。通過動手操作，學生明白可以將新知轉化為已學過的知識進行探究。于是教師提出問題讓學生運用轉化策略來解答，使學生從中感受到轉化策略的價值，促進學生對所學數學知識的理解。最后，教師引導學生回顧與梳理所學知識，鞏固學生的記憶。在教師的啟發下，除了平面圖形中運用到轉化策略外，學生還想到了是不是可以將小數除法和乘法轉化為整數進行計算。這樣教學，學生經歷了猜想、驗證的過程，積累了豐富的數學活動經驗，促進了數學知識的整體建構。

上述教學，教師從面積的概念入手，組織學生進行拼一拼、剪一剪等活動，于無形中向學生滲透轉化的思想方法，使學生真正感受到轉化策略的實用性，實現了數學知識的整體建構。

綜上所述，數學教學中，教師可從知識的整體關聯入手，引導學生不斷深入探究，促進學生的數學學習，使學生所學的數學知識形成一個有機的整體，實現從整體上提升學生數學核心素養的目的。

（責編 杜 華）