小學數學教學中數形結合思想的融入策略

陳福艷

摘 要 小學數學作為一門基礎且重要的學科，其具有一定的邏輯性和抽象性。將數形結合思想滲透到課堂教學中，不僅能夠降低學生學習難度，幫助其快速理解知識，還能夠將抽象的重難點生動形象化，大大提升課堂教學效率。本文就小學數學教學中數形結合思想的融入策略展開探討。

關鍵詞 小學數學 數形結合思想 教學

中圖分類號：G623.5文獻標識碼：A

數形結合涉及“形”與“數”，數形結合思想主要是指將小學生的具體形象思維過渡為抽象邏輯思維的重要方式，通過直觀清晰的圖形，幫助小學生分析問題、解決問題，從思想上降低學習難度。將數形結合思想滲透到小學數學課堂教學中，能夠將數和形進行結合，培養小學生核心素養，從不同的角度思考和理解知識，夯實學生知識基礎，實現課堂教學目標。

1借助數形結合，掌握數學概念

小學數學教材中涵蓋了大量的概念知識，并且各個概念之間還具有一定的關聯性。要想學好數學，學生首先就要深入理解概念，把握各個概念之間的相似性和差異性，為后續的學習奠定扎實的基礎。但是，由于小學生理解能力較弱，對于數學概念的學習存在一定難度。所以，教師就可以針對抽象的公式和概念，構建相應的表格或者圖形，遵循直觀性和簡潔性原則，通過直觀形象的方式，對各個概念進行歸納和總結，幫助小學生進一步理解和運用。

例如，在學習“分數的意義和性質”這一概念時，單純憑借教師口頭的講述學生無法理解其概念本質。因此教師就可以借助多媒體為學生創設一個主題情境，引導學生進行操作實踐。用圓形紙片替代蛋糕，將其沿直徑對折平分成2份，學生能夠在真實的操作中感知半個蛋糕就是蛋糕的二分之一，教師引導學生將該過程敘述出來，并說一說“另一半”的意思。然后，再次引導學生分析兩個半圓，感悟一個圓中有兩個二分之一，使學生完整建構二分之一的概念。通過這種方式，學生說出自己的操作過程能夠清楚的了解二分之一的由來，不僅使得學生有序思考，還循序漸進的幫助學生感知概念知識，達到事半功倍的教學成效。

2借助數形結合，解決應用計算

小學數學中計算題是常見的類型，隨著學習難度的增加，個別計算題也具有很強的邏輯性和思維性，如果學生馬虎大意，或是對題干理解不到位，都會造成計算結果錯誤。如果教師單一的將解題方法傳授給學生，學生只關注問題本身和數字，那么這種固化的計算教學方式，對于個別理解能力弱的學生來說，也具有一定難度。因此，利用數形結合思想，就能夠促使計算題目更加直觀形象，學生也能夠在腦海中，通過圖形分析快速形成解題思路，算出正確的答案。

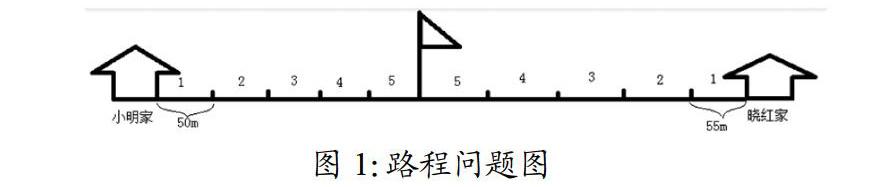
例如，路程問題是小學數學中一類重要問題類型，教師出示題目：“小明和曉紅分別同時從自己的家出發，相向而行，已知小明每分鐘行走50m，曉紅每分鐘行走55m，5分鐘后，曉紅和小明相遇，請問他們家之間的距離是多少？”然后，教師引導學生將每分鐘的步行距離作為一個線段單位，對應分鐘數繪制出相應的線段個數（如圖1），從而直觀的求出兩人的行走距離：50？=250m，55？=275m，250+275=525m。

3借助數形結合，明確數量關系

數學知識來源于生活，解決的問題也是生活中常見的。教師在設計教學內容的時候，需要緊貼學生生活實際，喚醒學生的已有經驗和認知，從而找準重難點突破口，幫助學生發散數學思維。尤其是針對數量關系較為隱蔽的數學問題來說，其更加容易混淆小學生的思維，通過數形結合的滲透，引導學生正確地分析數學題目，將復雜的數量關系直觀清晰的呈現出來，這一過程稱為“數形互譯”。

例如，一名農夫經營一片果園，其中已知桃樹380棵，桃樹是梨樹的2倍，蘋果樹是梨樹的3倍，請問蘋果樹有多少棵？在解決該類問題的時候，學生容易被數量關系所迷惑，而利用圖形將題干的主要內容繪制出來，就能夠直觀的幫助學生快速明確數量關系，從而得出答案。通過簡單的對應畫圖，學生能夠從中發現每句話對應一個等式，從而就能夠通過380？得到梨樹數量，再用梨樹數量？得出蘋果樹數量。每個解題步驟都清楚的展示出來，幫助學生形成適合自己的數學思維，為今后的解題奠定基礎。

4結語

在小學數學課堂上滲透數形結合思想，不僅符合新課改的要求，還強化了學生數學思維能力的鍛煉，提升課堂教學效率。教師要積極創新教學模式，采取多樣化的手段對數學課堂上存在的問題加以分析，結合“數字”和“圖形”之間的聯系，將抽象的數學語言與生動的圖形進行整合，全方位發掘小學生學習數學的思維能力、轉化能力以及創新能力。

參考文獻

[1] 林錦成.談小學生數形結合思維與運用能力培養[J].福建茶葉，2020，42（04）：256.

[2] 吳幼山.數形結合思想在小學數學教學中的應用[J].學周刊，2020（13）：141-142.