拉動(dòng)初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力” 增長(zhǎng)的“三駕馬車(chē)”

岳紹杰 于彬

[摘? 要] 文章以魯教版“3.3 勾股定理的應(yīng)用舉例（1）”為例，提出拉動(dòng)初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力”增長(zhǎng)的“三駕馬車(chē)”（問(wèn)題情境、追問(wèn)理答、變式教學(xué)）的初步設(shè)想，并給出簡(jiǎn)單的思考：?jiǎn)栴}情境——引導(dǎo)提出問(wèn)題，增強(qiáng)學(xué)習(xí)動(dòng)力;追問(wèn)理答——指向深度學(xué)習(xí)，鍛煉學(xué)習(xí)毅力;變式教學(xué)——培養(yǎng)高階思維，提升數(shù)學(xué)能力.

[關(guān)鍵詞] 勾股定理;問(wèn)題情境;追問(wèn)理答;變式教學(xué);學(xué)習(xí)力

“學(xué)習(xí)力”特指學(xué)習(xí)的動(dòng)力、毅力和能力，其中學(xué)習(xí)的能力是一種可培養(yǎng)、可預(yù)見(jiàn)的能力，我們認(rèn)為初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力”，特別是學(xué)習(xí)能力方面主要表現(xiàn)在能夠在深度學(xué)習(xí)中，提出具有高階思維含量的數(shù)學(xué)問(wèn)題.

“三駕馬車(chē)”原指拉動(dòng)經(jīng)濟(jì)增長(zhǎng)的投資、消費(fèi)和出口，那么在初中數(shù)學(xué)課堂中有沒(méi)有拉動(dòng)初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力”增長(zhǎng)的“三駕馬車(chē)”呢？在長(zhǎng)期的初中數(shù)學(xué)教學(xué)實(shí)踐中我們認(rèn)為“問(wèn)題情境、追問(wèn)理答、變式教學(xué)”對(duì)提高初中數(shù)學(xué)課堂的教學(xué)效益起著至關(guān)重要的作用，應(yīng)該是拉動(dòng)初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力”增長(zhǎng)的“三駕馬車(chē)”.

魯教版“3.3 勾股定理的應(yīng)用舉例（1）”主要涉及勾股定理逆定理和最短路徑問(wèn)題，課堂教學(xué)容量大、知識(shí)點(diǎn)難度大，理解起來(lái)比較抽象. 在一次市級(jí)教研員優(yōu)質(zhì)課評(píng)比中筆者有幸執(zhí)教該課，在團(tuán)隊(duì)成員的幫助和個(gè)人的努力下，主要從“問(wèn)題情境、追問(wèn)理答、變式教學(xué)”三個(gè)方面（“三駕馬車(chē)”）仔細(xì)打磨，認(rèn)真設(shè)計(jì)了這節(jié)課，最終取得了優(yōu)異的成績(jī). 下面進(jìn)行簡(jiǎn)單的介紹，不當(dāng)之處，敬請(qǐng)指正.

教材簡(jiǎn)析

“3.3 勾股定理的應(yīng)用舉例（1）”是魯教版初中數(shù)學(xué)七年級(jí)上冊(cè)第三章“勾股定理”第三節(jié)的第一課時(shí)，這節(jié)課是在學(xué)生掌握了勾股定理以及如何判斷一個(gè)三角形是否是直角三角形（勾股定理逆定理）之后進(jìn)行的教學(xué)內(nèi)容，主要涉及利用勾股定理解決圓柱或長(zhǎng)方體（正方體）中的最短路徑問(wèn)題，以及利用勾股定理逆定理判斷一個(gè)三角形是否是直角三角形兩類(lèi)問(wèn)題.

教材中首先呈現(xiàn)最短路徑問(wèn)題，通過(guò)四個(gè)問(wèn)題，從“側(cè)面爬”到沿“表面爬”，引導(dǎo)學(xué)生在動(dòng)手實(shí)踐和操作中獲得此類(lèi)問(wèn)題的解決方法;然后以實(shí)際問(wèn)題的形式，引導(dǎo)學(xué)生在自己首先提出解決問(wèn)題方法基礎(chǔ)上，再利用勾股定理逆定理判斷李叔叔方法的合理性，符合新教材的設(shè)計(jì)理念. 在實(shí)際教學(xué)中根據(jù)學(xué)生的實(shí)際認(rèn)知水平，我們對(duì)教材進(jìn)行了整合，將上述兩個(gè)問(wèn)題的呈現(xiàn)順序進(jìn)行了互換，即先呈現(xiàn)與勾股定理逆定理有關(guān)的問(wèn)題，然后再集中力量解決最短路徑問(wèn)題，這種對(duì)教材的整合處理方式，旨在引導(dǎo)學(xué)生先從平面內(nèi)分析和解決問(wèn)題，再?gòu)目臻g內(nèi)分析和解決問(wèn)題，遵循“平面——立體——平面”的認(rèn)知邏輯關(guān)系，使學(xué)生能夠形成在平面內(nèi)解決問(wèn)題的基本方法，同時(shí)為學(xué)生能將立體圖形轉(zhuǎn)化為平面圖形提供了可能，順利實(shí)現(xiàn)“化曲為直”，體會(huì)轉(zhuǎn)化的數(shù)學(xué)思想，收到了良好的課堂教學(xué)效果.

教學(xué)設(shè)計(jì)簡(jiǎn)述

1. 創(chuàng)設(shè)情境

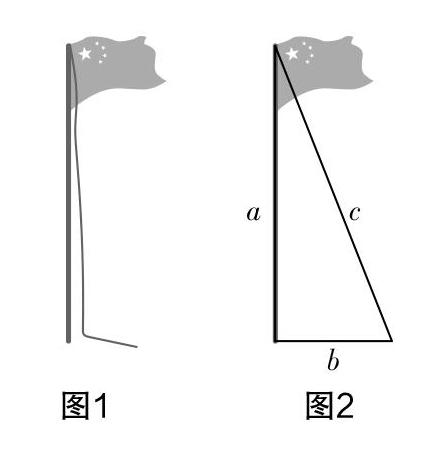
下圖是學(xué)校的旗桿示意圖，旗桿上的繩子垂到了地面，并余出了一段（如圖1）;某同學(xué)把繩子拉直后，繩子末端恰好落在地面上（如圖2），根據(jù)圖形，你能提出什么數(shù)學(xué)問(wèn)題？

設(shè)計(jì)意圖? 用國(guó)慶70周年微視頻直觀震撼，拉近數(shù)學(xué)和現(xiàn)實(shí)生活的距離，激發(fā)學(xué)生的好奇心和求知欲，讓學(xué)生充分感受到實(shí)際生活問(wèn)題與數(shù)學(xué)知識(shí)的聯(lián)系，讓學(xué)生自己提出數(shù)學(xué)問(wèn)題，引起學(xué)生的探索欲望，培養(yǎng)學(xué)生的愛(ài)國(guó)主義情懷.

2. 定理再現(xiàn)

定理再現(xiàn) （1）：（兩點(diǎn)之間線(xiàn)段最短）有一個(gè)長(zhǎng)方形的公園如圖3所示，由景點(diǎn)A 到景點(diǎn)C 哪條路徑最短呢？最短路徑是多少千米？

定理再現(xiàn)（2）：（勾股定理逆定理）如圖4，李叔叔想要檢測(cè)雕塑底座正面的AD邊和BC邊是否分別垂直于底邊AB，但他隨身只帶了卷尺.

①你能替他想辦法完成任務(wù)嗎？

②李叔叔量得AD長(zhǎng)是30厘米，AB長(zhǎng)是40厘米，BD長(zhǎng)是50厘米，AD邊垂直于AB邊嗎？為什么？

③小明隨身只有一個(gè)長(zhǎng)度為20厘米的刻度尺，他能有辦法檢驗(yàn)邊AD是否垂直于邊AB嗎？邊BC與邊AB呢？

設(shè)計(jì)意圖? 通過(guò)提出數(shù)學(xué)問(wèn)題引出本節(jié)課所需要的基礎(chǔ)知識(shí)勾股定理以及勾股定理逆定理，通過(guò)“定理再現(xiàn)（1）”將“兩點(diǎn)之間，線(xiàn)段最短”和勾股定理聯(lián)系在一起;通過(guò)“定理再現(xiàn)（2）”的雕塑情境，使學(xué)生感悟體會(huì)數(shù)形結(jié)合的思想. 在問(wèn)題解決過(guò)程中，使學(xué)生體會(huì)數(shù)學(xué)是解決實(shí)際問(wèn)題和進(jìn)行交流的重要工具，在現(xiàn)實(shí)生活中有廣泛的應(yīng)用，培養(yǎng)學(xué)生學(xué)數(shù)學(xué)、用數(shù)學(xué)的意識(shí).

3. 自主探究

活動(dòng)要求：請(qǐng)同學(xué)們拿出已做好的圓柱，在圖上（如圖5）標(biāo)出點(diǎn)A、點(diǎn)B的位置，嘗試著從點(diǎn)A到點(diǎn)B沿圓柱表面畫(huà)出幾條路線(xiàn)，你覺(jué)得哪條路線(xiàn)最短呢？請(qǐng)說(shuō)出你的理由.

（1）自主嘗試：學(xué)生自己獨(dú)立思考，能想出幾種路線(xiàn).

（2）交流互助（小組）：在小組內(nèi)的圓柱模型上畫(huà)一畫(huà)，小組內(nèi)交流.

（3）展示講解（班內(nèi)）：小組展示各自的圓柱模型上所畫(huà)路線(xiàn)，體會(huì)展開(kāi)圖中直角三角形的兩條直角邊與圓柱的底面周長(zhǎng)、高之間的聯(lián)系.

（4）定理應(yīng)用：在情境上給出相應(yīng)的數(shù)據(jù)，應(yīng)用定理進(jìn)行計(jì)算. 已知圓柱的高是12厘米，底面圓的周長(zhǎng)是18厘米，求小蟲(chóng)在圓柱外面爬行的最短路程是多少厘米.

方法提煉（如圖6）：（1）展成平面圖形（化曲為直）;（2）確定最短路線(xiàn)（兩點(diǎn)之間，線(xiàn)段最短）;（3）利用勾股定理求解（建立模型）.

設(shè)計(jì)意圖? 借助信息技術(shù)平臺(tái)，將情境利用Flash播放，增加趣味性，調(diào)動(dòng)學(xué)生的積極性;在學(xué)生經(jīng)歷了自主思考的基礎(chǔ)上，進(jìn)行有效的小組活動(dòng)，突破本節(jié)難點(diǎn). 在此環(huán)節(jié)讓學(xué)生充分體會(huì)“化曲為直”的轉(zhuǎn)化思想.

4. 鞏固提升

變式訓(xùn)練：有一圓柱形油罐如圖7所示，已知油罐的底面圓半徑是2米，高是5米，要從A點(diǎn)起環(huán)繞油罐建梯子，梯子的頂端正好到達(dá)A點(diǎn)的正上方B點(diǎn)，則梯子最少需要多少米？（π≈3）

終極挑戰(zhàn)：如圖8，一個(gè)長(zhǎng)方體盒子，它的長(zhǎng)、寬、高分別為8厘米、8厘米、12厘米，一只螞蟻想（沿側(cè)面）從盒底的點(diǎn)A爬到盒頂?shù)狞c(diǎn)B，最短路徑是多少？

設(shè)計(jì)意圖? 通過(guò)變式訓(xùn)練，讓學(xué)生進(jìn)一步體會(huì)“化曲為直”的轉(zhuǎn)化思想，培養(yǎng)學(xué)生分析問(wèn)題和解決問(wèn)題的能力，掌握問(wèn)題解決的方法途徑，在變化中尋求不變，抽取一般規(guī)律，體會(huì)學(xué)科的應(yīng)用價(jià)值.

5.感悟體會(huì)

設(shè)計(jì)意圖? 留給學(xué)生充分的時(shí)間和空間，培養(yǎng)學(xué)生歸納概括的能力. 教師用思維導(dǎo)圖的形式（比如圖9）進(jìn)行總結(jié)歸納，幫助學(xué)生把零散的知識(shí)串起來(lái)，幫助學(xué)生理解.

6. 布置作業(yè)

（1）鞏固性作業(yè)：略.

（2）拓展性作業(yè)：略.

（3）實(shí)踐性作業(yè)：借助勾股定理，利用升旗的繩子，卷尺，請(qǐng)你設(shè)計(jì)一個(gè)方案，測(cè)算出旗桿的高度.

課下寄語(yǔ)：把勾股定理送到外星球，與外星人進(jìn)行數(shù)學(xué)交流 ！——華羅庚; 學(xué)好數(shù)學(xué)，用數(shù)學(xué)的眼光觀察世界，用數(shù)學(xué)與世界進(jìn)行對(duì)話(huà)！——岳紹杰.？搖？搖

設(shè)計(jì)意圖? 鞏固所學(xué)，使課堂向課外延伸. 通過(guò)課下寄語(yǔ)，引導(dǎo)學(xué)生喜歡數(shù)學(xué)，體會(huì)數(shù)學(xué)在解決現(xiàn)實(shí)生活實(shí)際問(wèn)題中所發(fā)揮的重要作用.

幾點(diǎn)思考

1. 問(wèn)題情境：引導(dǎo)提出問(wèn)題，增強(qiáng)學(xué)習(xí)動(dòng)力

好的問(wèn)題情境，可以引發(fā)學(xué)生思考，起到事半功倍的效果，因此本節(jié)課以建國(guó)70周年慶典中升旗儀式的視頻引入新課，意在調(diào)動(dòng)學(xué)生學(xué)習(xí)的積極性和主動(dòng)性，同時(shí)厚植學(xué)生的愛(ài)國(guó)情懷. 此外，這個(gè)情境貫穿教學(xué)的始終，與作業(yè)布置環(huán)節(jié)的實(shí)踐性作業(yè)前后照應(yīng)，形成了課堂教學(xué)的“閉環(huán)”，學(xué)生很希望可以獨(dú)立解決這個(gè)問(wèn)題，進(jìn)而可以很好地增強(qiáng)學(xué)生的學(xué)習(xí)動(dòng)力.

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》在重視分析問(wèn)題和解決問(wèn)題的基礎(chǔ)上，更加重視學(xué)生發(fā)現(xiàn)問(wèn)題和提出問(wèn)題的能力，意在實(shí)現(xiàn)“兩能”到“四能”的突破. 因此本課在開(kāi)課之初的“創(chuàng)設(shè)情境”中就以“你能提出什么數(shù)學(xué)問(wèn)題？”讓學(xué)生嘗試著結(jié)合情境自己提出問(wèn)題，然后解決自己提出的問(wèn)題. 這樣開(kāi)放性的設(shè)問(wèn)可以增強(qiáng)學(xué)生對(duì)數(shù)學(xué)的學(xué)習(xí)興趣，特別是解決自己提出的問(wèn)題后的喜悅，能夠進(jìn)一步增強(qiáng)學(xué)生的學(xué)習(xí)動(dòng)力.

2. 追問(wèn)理答：指向深度學(xué)習(xí)，鍛煉學(xué)習(xí)毅力

追問(wèn)理答是一線(xiàn)教師教學(xué)的基本功，再好的課堂預(yù)設(shè)在實(shí)際教學(xué)中都有可能會(huì)出現(xiàn)“意外”，面對(duì)這樣的“意外”，更能看出一個(gè)教師的教學(xué)機(jī)智.

本節(jié)課的“自主探究”環(huán)節(jié)是本節(jié)課的重中之重，是本節(jié)課教學(xué)難點(diǎn)突破的關(guān)鍵環(huán)節(jié)，此環(huán)節(jié)的成敗決定著本節(jié)課的成敗，而這個(gè)探究環(huán)節(jié)是一個(gè)開(kāi)放性的探究問(wèn)題，課堂教學(xué)中很可能會(huì)出現(xiàn)教師意想不到的情況，因此在教學(xué)前我們做了充分的預(yù)設(shè)（追問(wèn)與理答），保證了課堂教學(xué)中的精彩生成.

比如，在“自主探究”環(huán)節(jié)的“交流互助”中，引導(dǎo)學(xué)生將圓柱沿著母線(xiàn)展開(kāi)是關(guān)鍵性的一環(huán)，此時(shí)執(zhí)教教師并沒(méi)有直接告訴學(xué)生，而是讓學(xué)生動(dòng)手實(shí)踐、自主探究，經(jīng)歷問(wèn)題發(fā)現(xiàn)的全過(guò)程，體會(huì)到在側(cè)面上畫(huà)兩點(diǎn)之間的路線(xiàn)非常困難. 甚至在學(xué)生發(fā)現(xiàn)“沿著側(cè)面不好畫(huà)”的情況下也沒(méi)有急切地告訴學(xué)生解決問(wèn)題的方法，而是以一句“按照你認(rèn)為好畫(huà)的方法來(lái)畫(huà)！”理答學(xué)生提出的疑問(wèn)，進(jìn)而順利“逼”出了問(wèn)題的答案——“展開(kāi)畫(huà)”！強(qiáng)化了學(xué)生自主學(xué)習(xí)的意識(shí)，實(shí)現(xiàn)了深度學(xué)習(xí)，達(dá)到了很好的課堂教學(xué)效果.

再比如，在“自主探究”環(huán)節(jié)的“展示講解”中，執(zhí)教教師耐心引領(lǐng)，在學(xué)生“卡殼”后，一句近似口語(yǔ)的“再‘圍起來(lái)看看”，激發(fā)了學(xué)生進(jìn)一步的探究熱情，讓學(xué)生在動(dòng)手操作中實(shí)現(xiàn)思考的進(jìn)一步深入，促進(jìn)學(xué)生的深度思考，鍛煉學(xué)生的學(xué)習(xí)毅力.

3. 變式教學(xué)：培養(yǎng)高階思維，提升數(shù)學(xué)能力

變式教學(xué)是中國(guó)數(shù)學(xué)教學(xué)的特色，變式教學(xué)可以培養(yǎng)高階思維，提升學(xué)生的數(shù)學(xué)能力，在本課例中有很好的體現(xiàn).

“定理再現(xiàn)（2）”中的問(wèn)題③的提出就是問(wèn)題②的變式，在鞏固問(wèn)題②的解決方法的基礎(chǔ)上，引導(dǎo)學(xué)生提出更多的解決辦法，促進(jìn)學(xué)生的進(jìn)一步思考，體現(xiàn)數(shù)學(xué)問(wèn)題解決方式的多樣性.

“自主探究”環(huán)節(jié)我們將教材中設(shè)計(jì)的四個(gè)問(wèn)題（從“側(cè)面爬”到沿“表面爬”的“腳手架”問(wèn)題）改為了“沿圓柱表面畫(huà)出幾條路線(xiàn)，你覺(jué)得哪條路線(xiàn)最短呢？”以此開(kāi)闊學(xué)生的視野，體現(xiàn)分類(lèi)討論的數(shù)學(xué)思想，使學(xué)生的思維更加嚴(yán)密. “鞏固提升”中的變式訓(xùn)練是對(duì)此題的進(jìn)一步強(qiáng)化，將解決問(wèn)題的數(shù)學(xué)模型進(jìn)一步完善和豐富，為類(lèi)似問(wèn)題的解決奠定堅(jiān)實(shí)的基礎(chǔ). “終極挑戰(zhàn)”中的問(wèn)題由“沿側(cè)面”到“沿表面”進(jìn)行變式設(shè)置，呈現(xiàn)載體由“圓柱”到“立方體”，對(duì)學(xué)生的思維能力提出了更高的要求，起到了變式教學(xué)應(yīng)有的效果，值得其他一線(xiàn)教師積極踐行.

我們通過(guò)一節(jié)課對(duì)拉動(dòng)初中學(xué)生數(shù)學(xué)“學(xué)習(xí)力”增長(zhǎng)的“問(wèn)題情境、追問(wèn)理答、變式教學(xué)”（“三駕馬車(chē)”）進(jìn)行了簡(jiǎn)單的介紹，未必準(zhǔn)確，更不一定正確，歡迎更多的一線(xiàn)教師參與進(jìn)來(lái)，開(kāi)發(fā)出更多的優(yōu)秀案例.