轉(zhuǎn)化思想在小學(xué)數(shù)學(xué)“空間與圖形”中的應(yīng)用
何靜


摘要:教育部[1]義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2011)提出把數(shù)學(xué)教學(xué)中的基礎(chǔ)知識、基本技能、基本思想和基本經(jīng)驗(yàn)作為小學(xué)數(shù)學(xué)課程的總體目標(biāo)。其中轉(zhuǎn)化思想是其他數(shù)學(xué)思想的基礎(chǔ)。而“空間與圖形”作為小學(xué)數(shù)學(xué)教材中的四大板塊之一,在小學(xué)數(shù)學(xué)內(nèi)容中占據(jù)重要地位,是小學(xué)數(shù)學(xué)教學(xué)中的重難點(diǎn),也是大部分學(xué)生最易出錯(cuò)的板塊,通過研究如何在“空間與圖形”中應(yīng)用轉(zhuǎn)化思想,讓學(xué)生把握轉(zhuǎn)化的本質(zhì)屬性,排除非本質(zhì)屬性的干擾在解題中會(huì)正確應(yīng)用轉(zhuǎn)化的思想去解決數(shù)學(xué)問題。
關(guān)鍵詞:小學(xué)數(shù)學(xué);空間與圖形;轉(zhuǎn)化思想
1引言
1.1研究背景
新課程標(biāo)準(zhǔn)指出,新知轉(zhuǎn)化成舊知,復(fù)雜難學(xué)的問題轉(zhuǎn)化成簡單易學(xué)問題的都是基于學(xué)生認(rèn)知發(fā)展水平對數(shù)學(xué)教學(xué)活動(dòng)的要求,數(shù)學(xué)教學(xué)目標(biāo)強(qiáng)調(diào)學(xué)生在學(xué)習(xí)中能夠理解和運(yùn)用學(xué)習(xí)的思想和方法。小學(xué)數(shù)學(xué)教材內(nèi)容的編寫滲透了許多轉(zhuǎn)化為老師在教學(xué)中滲透轉(zhuǎn)化思想提供了機(jī)會(huì),如果教師認(rèn)真進(jìn)行歸納梳理教材內(nèi)容,會(huì)發(fā)現(xiàn)小學(xué)教材空間和圖形模塊數(shù)學(xué)知識總是與前后知識有所聯(lián)系,存在共性,教學(xué)中滲透轉(zhuǎn)化思想幫助學(xué)生理解掌握。
2轉(zhuǎn)化思想在空間與圖形中的應(yīng)用
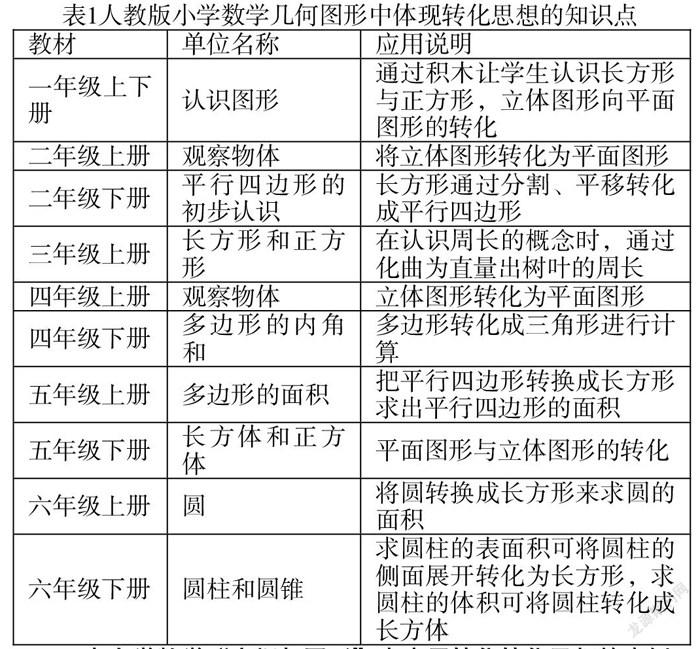
表1人教版小學(xué)數(shù)學(xué)幾何圖形中體現(xiàn)轉(zhuǎn)化思想的知識點(diǎn)
3.在小學(xué)數(shù)學(xué)“空間與圖形”中應(yīng)用轉(zhuǎn)化轉(zhuǎn)化思想的案例分析
3.1“化繁為簡”的案例應(yīng)用分析。數(shù)學(xué)家波利亞提出“當(dāng)原來的問題不可解決時(shí),不要忘記人類的高明之處就在于迂回繞過不能直接克服的障礙,在于能想出某些適當(dāng)?shù)妮o助問題。”復(fù)雜的問題通常是由幾個(gè)簡單的問題組合而成,在小學(xué)數(shù)學(xué)圖形解題過程中,用作幾何圖形輔助線的方法,可以清楚直觀的將復(fù)雜問題轉(zhuǎn)化成簡單問題,提高學(xué)生的解題速度。
在講解五年級多邊形面積習(xí)題時(shí),有一道這樣的題:如下圖所示,一個(gè)平行四邊被分成甲、乙兩部分,甲的面積比乙大24m2。甲的上底是多少米?
圖1例題圖示
老師帶著學(xué)生分析:由圖可知,甲圖是一個(gè)梯形,乙圖是一個(gè)三角形,要求梯形的上底,我們不僅可以算出梯形的面積根據(jù)公式計(jì)算上底還可以間接的先求出三角形面積,得到三角形的底,最后求出梯形的上底。提問學(xué)生你是怎樣計(jì)算?你有幾種方法進(jìn)行計(jì)算?請列式說說你的計(jì)算過程
學(xué)生一:20×8-24=136(平方米),136÷8=17(米),20-17=3(米)。
學(xué)生的算式似乎并不復(fù)雜可經(jīng)歷了較復(fù)雜的思考過程:先計(jì)算出平行四邊形的面積減去甲比乙多的面積24m2,得到由兩個(gè)相同大小的三角形組成的平行四邊形的面積,用它的面積除以高得到三角形的底,最后用平行四邊形的底減去三角形的底得到梯形的底。
學(xué)生二:20×8-24=136(平方米)136÷2+24=92平方米),92×2÷8-20=3(米)。
這樣的解題過程同樣復(fù)雜,學(xué)生通過梯形的面積公式逆向運(yùn)算求上底。第一步和第一位同學(xué)一樣得到兩個(gè)相同三角形的組成的面積,再求出一個(gè)三角形的面積加上多出的面積得到梯形的面積,最后根據(jù)面積逆運(yùn)算公式推出梯形的上底。
學(xué)生三:(20×8-24)÷2=68(平方米),68×2÷8=17(米),20-17=3(米)。
學(xué)生的思維過程同樣先計(jì)算出一個(gè)三角形的面積,然后計(jì)算三角形的底,最后求出梯形的上底。這種方法與第一個(gè)學(xué)生的方法類似,還是首先計(jì)算出三角形的底,有所不同之處在于第一種解法是利用組成平行四邊形面積求出三角形的底,這里是直接求出三角形面積,然后求底。老師的引導(dǎo)方向也卻是如此,想要學(xué)生們能熟練的掌握不同的推導(dǎo)過程,并將不同的計(jì)算方式進(jìn)行板書和詳細(xì)分析,教會(huì)學(xué)生運(yùn)用不同的思維進(jìn)行解題,強(qiáng)調(diào)的是讓學(xué)生掌握多種計(jì)算方法和對面積公式的熟練忽略了在多邊形面積計(jì)算過程中滲透化繁為簡的轉(zhuǎn)化思想,大大降低了學(xué)生的做題速度和學(xué)習(xí)效率。下面我將針對本題如何進(jìn)行化繁為簡的轉(zhuǎn)化思想應(yīng)用進(jìn)行分析如下:
從上述學(xué)生們的的解題思路過程分析可知在該教師的指導(dǎo)下他們對多邊形的面積計(jì)算及推導(dǎo)過程以及相當(dāng)熟練了。但是,存在的問題是解題的思維過程十分復(fù)雜,這在于做題時(shí)會(huì)浪費(fèi)大量的時(shí)間降低學(xué)生的學(xué)習(xí)興趣和學(xué)習(xí)效率,不利于學(xué)生數(shù)學(xué)思想方法的吸收。然后如果該教師在教學(xué)時(shí)應(yīng)用化繁為簡的轉(zhuǎn)化思想在圖上添加一條輔助線,在甲圖中畫一個(gè)與乙完全相同的三角形畫(如下圖),問題就迎刃而解。
圖2解題思路圖
從圖中知,甲比乙多的24m2正好是一個(gè)平行四邊形,這個(gè)平行四邊形的底正好是原梯形的上底,所以梯形的上底是:24÷8=3(米)這樣便能快速解決問題,并且能有效提高學(xué)生的數(shù)學(xué)思維。
3.2“化曲為直”的案例應(yīng)用分析。邁克爾等人將學(xué)習(xí)分為認(rèn)知策略、元認(rèn)知策略和資源管理策略,認(rèn)知策略則是將新知識通過加工處理找到與已有知識的聯(lián)系。在小學(xué)數(shù)學(xué)曲線圖形學(xué)習(xí)中就要求學(xué)生能夠掌握將圖形信息進(jìn)行加工,并且在知識學(xué)習(xí)的過程中通過模型直觀過程中培養(yǎng)學(xué)生的觀察能力進(jìn)行有效信息提取加工將新學(xué)材料與頭腦中已有知識聯(lián)系起來達(dá)到學(xué)習(xí)效果。人教版六年級上冊教材編排“圓的面積”通過回憶以前用的轉(zhuǎn)化方法把圓的面積轉(zhuǎn)化成熟悉的直線圖形的面積來計(jì)算。
結(jié)語:綜合以上轉(zhuǎn)化即保持事物本質(zhì)不變的情況下改變它的形式,在小學(xué)階段空間與圖形板塊內(nèi)容較多,而且并不是所有內(nèi)容都蘊(yùn)含著轉(zhuǎn)化思想或者都適合應(yīng)用轉(zhuǎn)化思想,通過分析研究轉(zhuǎn)化思想在空間與圖形中不同表現(xiàn)形式的應(yīng)用,幫助教師在教學(xué)中把握其本質(zhì)和內(nèi)在聯(lián)系,實(shí)現(xiàn)教學(xué)目的;幫助學(xué)生完成在學(xué)習(xí)過程中的再發(fā)現(xiàn)再創(chuàng)造,培養(yǎng)學(xué)生的創(chuàng)新意識;幫助學(xué)生建立和完善知識體系提高教學(xué)效率,從而實(shí)現(xiàn)數(shù)學(xué)化的過程。
參考文獻(xiàn):
[1]中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)[M](2011年版).北京:北京師范大學(xué)出版社,2011,8~9.

