從直觀想象到邏輯推理的數(shù)學(xué)概念課教學(xué)設(shè)計

余鐵青

【摘要】利用直觀想象與邏輯推理得到奇偶函數(shù)所具有的一般化特點。以此過程培養(yǎng)學(xué)生大膽猜想，仔細論證的思維品質(zhì)，樹立學(xué)生對數(shù)學(xué)“始于猜想，終于推理論證”的數(shù)學(xué)發(fā)展的科學(xué)認識。

【關(guān)鍵詞】直觀想象;邏輯推理;概念教學(xué);奇偶性;生成性

一、引言

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版）》就是在大力倡導(dǎo)建構(gòu)學(xué)生核心素養(yǎng)的背景下進行的修訂，明確提出了六大數(shù)學(xué)核心素養(yǎng)：數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、直觀想象、數(shù)學(xué)運算、數(shù)據(jù)分析。筆者基于實際發(fā)現(xiàn)直觀想想素養(yǎng)和邏輯推理素養(yǎng)的培養(yǎng)目標(biāo)就是讓學(xué)生學(xué)會用數(shù)學(xué)的眼光觀察世界，用數(shù)學(xué)的思維分析世界，并且能夠用數(shù)學(xué)的語言表達世界。

邏輯推理是由已經(jīng)總結(jié)出來的規(guī)律推出新的規(guī)律，是得到數(shù)學(xué)結(jié)論、構(gòu)建數(shù)學(xué)體系的重要方式，是數(shù)學(xué)嚴謹性的基本保證，是人們在數(shù)學(xué)活動中進行交流的基本思維品質(zhì)。

二、教學(xué)內(nèi)容背景分析與教學(xué)目標(biāo)

函數(shù)的奇偶性是繼函數(shù)單調(diào)性之后函數(shù)又一基本性質(zhì)，學(xué)生通過復(fù)習(xí)函數(shù)單調(diào)性的相關(guān)性質(zhì)，引導(dǎo)學(xué)生思考函數(shù)圖像的對稱性質(zhì)，并能根據(jù)所學(xué)知識掌握判定函數(shù)的奇偶性一般方法。與此同時發(fā)展學(xué)生類比，遷移，歸納總結(jié)和演繹推理的基本數(shù)學(xué)思維品質(zhì)。

三、教學(xué)重難點

重點：1.通過具體函數(shù)圖像的對稱性得到一般化的函數(shù)對稱性質(zhì)，并形成奇偶性概念;2.能夠不畫圖的基礎(chǔ)上判定函數(shù)的奇偶性。

難點：將圖像語言向符號語言過渡，即從形到數(shù)的抽象邏輯推理。

四、具體教學(xué)設(shè)計過程

1.晴境問題引入，形成直觀感知

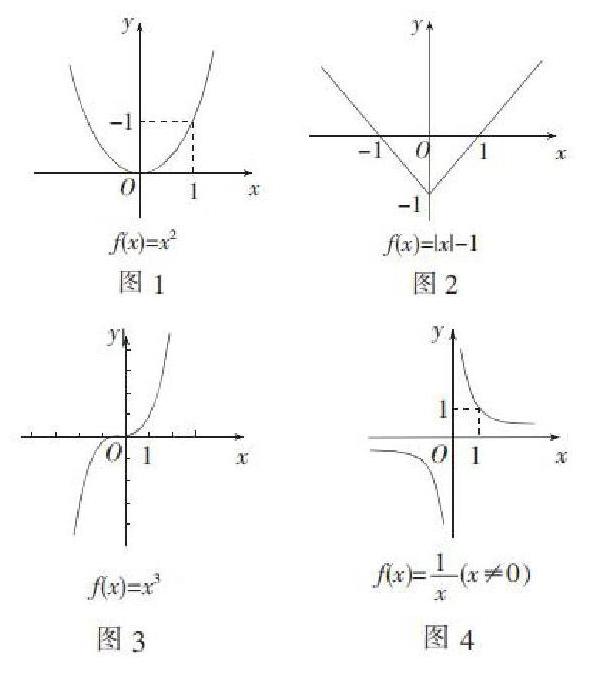
師：函數(shù)是刻畫變量間關(guān)系的數(shù)學(xué)模型，而圖像則能夠直觀的反映函數(shù)的變化趨勢等特征，請大家觀察以下四個圖形，我們分別把圖1和圖2分成一組，再把圖3和圖4分成一組，從單調(diào)性的角度你發(fā)現(xiàn)了什么？

設(shè)計意圖：第一，依據(jù)奇偶性把四個圖形分成兩組，更加有利于圖像的直觀對比與發(fā)散猜想。從函數(shù)的形人手，而這四個圖像中圖4的定義域不是R，為后面總結(jié)提煉判定函數(shù)奇偶性要注意的問題創(chuàng)設(shè)伏筆;第二，利用學(xué)生剛學(xué)過的函數(shù)單調(diào)性進行知識回顧，讓學(xué)生產(chǎn)生成功分析之后的強烈的成就感，并會主動形成對新知識的求知欲望，為進入學(xué)習(xí)新知識做準(zhǔn)備。

生1：根據(jù)前面我們所學(xué)的函數(shù)單調(diào)性看，圖1和圖2都是在（-∞，0）單調(diào)遞減，在（0，+∞）上單調(diào)遞增;而圖3在整個R上是增函數(shù)，圖4在（-∞，0）和（0，+∞）都是單調(diào)遞減的。

師：大家能根據(jù)前面所學(xué)，具體說說為什么圖1在（-∞，0）上是單調(diào)遞減的嗎？

生2：從圖像直觀上看，隨著x的增大，y在減小。

師：說的很好！但數(shù)學(xué)光有直觀觀察是不夠的，大家能用嚴謹?shù)臄?shù)學(xué)語言進行敘述嗎？

設(shè)計意圖：訓(xùn)練學(xué)生從直觀想象到理論推導(dǎo)的數(shù)學(xué)思考問題的方式，能夠?qū)⒅庇^語言轉(zhuǎn)化成嚴謹?shù)臄?shù)學(xué)語言進行翻譯，培養(yǎng)學(xué)生將自己所思所想通過筆頭上的數(shù)學(xué)化的表示出來。

生3：我們可以考慮在區(qū)間（-∞，0）上任取兩個不等實數(shù)x₁和x₂，不妨假設(shè)x₁2