重視基本圖形學會轉化劃歸
吳潔慧
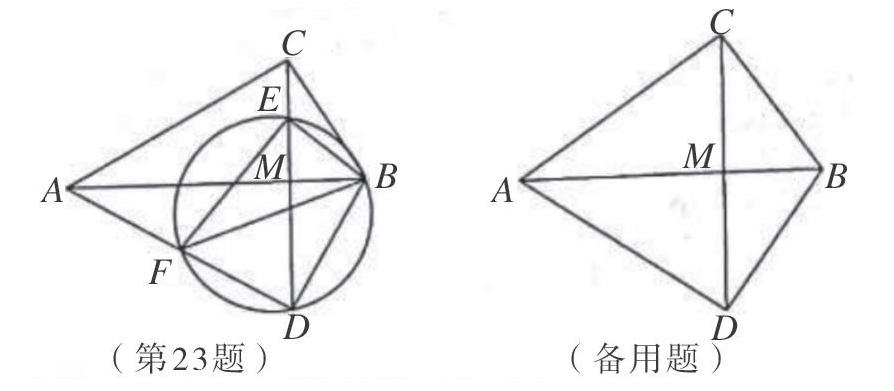

摘要:圓在初中平面幾何中是非常重要的一塊內容,近年來中考中往往和三角形、四邊形結合命題,2020年浙江臺州數學中考的第23題就是這樣一道在圓背景下的幾何綜合題。本題的解決需要學生具備一定的直觀想象、數學建模、邏輯推理、數學運算等核心素養。整理了此題的多種解法,并對試題導向進行了一定的分析。
關鍵詞:基本圖形;轉化;劃歸;方程;數學建模
一、試題呈現
(2020臺州中考第23題)如圖,在△ABC中,∠ABC=90°,將△ABC沿直線AB翻折得到△ABD,連接CD交AB于點M,E是線段CM上的點,連接BE,F是△BDE的外接圓與AD的另一個交點,連接EF,BF.
(1)求證:△BEF是直角三角形;
(2)求證:△BEF∽△BCA;
(3)當AB=6,BC=m時,在線段CM上存在點E,使得EF和AB互相平分,求m的值.
二、基于核心素養的試題評價
(一)關注核心內容,全面考查基礎
本題以圓為背景,全面考查了初中階段“圖形與幾何”的核心內容,特別是三角形的相關內容,這些內容都是初中階段課標要求的基礎知識和基本技能。第(1)題考查了“翻折”—軸對稱的性質、直角三角形的判定。第(2)題考查了相似三角形的判定。第(3)題考查了相似三角形的性質與判定、平行四邊形(矩形)的性質與判定、勾股定理、垂徑定理的應用。特別是“EF和AB互相平分”也就是線段的特殊的數量關系,由此得到直線AF和BE“平行”的特殊的位置關系,再確定動點E的位置,從而確定BC的長度,符合幾何從一般到特殊的研究規律。這小題中考查了初中求線段的幾種基本方法,特別是利用相似三角形找線段的比例關系、建立方程并求解這種一般路徑。這是初中生必須掌握的基本方法和基本技能。
本題的第(2)小題的圖形中,有很多學生在平時練習中遇到并總結過的基本圖形。題干中的“箏形”來自人教版教材八年級上的全等三角形,圓內接四邊形的圖來自于九年級上的內容,第(3)小題的線段計算則可以用到“母子相似”“A子字形相似”“X字形相似”“共邊共角型相似”等相似三角形的基本圖形。這些基本圖形,能幫助學生順利地進行轉化劃歸,將圓背景的綜合問題轉化到三角形問題去解決,因此此題對學生分析解決問題的能力提出了較高要求。
(二)凸顯思想方法,直擊核心素養
這是一題圓背景的幾何綜合題,本題的解決需要學生具備一定的邏輯推理、幾何直觀、數學運算、數學建模等核心素養,對學生幾何的四基和四能有很好的檢驗和評價作用。特別第(3)小問的求值問題,需要學生在復雜幾何圖形中發現基本圖形,并利用相似三角形的性質或者勾股定理等基本方法建立方程模型求解,綜合考查了直觀想象和數學建模的素養,也考查了轉化劃歸的數學基本思想方法。同時,由于點 E 是動點,由它的特殊性需要在備用圖中畫出準確圖形,也考查了學生基本課堂活動經驗的積累,只有能相對準確畫出圖形的學生才會發現由EF和AB互相平分可以得到EB∥AD,加上第(1)小題得到的∠BEF是直角,可知四邊形EFDB是特殊四邊形矩形這個結論,才能根據“射影定理”“勾股定理”等建立方程模型,因此平時的教學我們一定要重視學生的動手畫圖能力,積累必需的作圖經驗,要讓學生經歷知識的發生過程,明確定理使用的條件。
三、部分多解、優解賞析
(一)第(1)題的解法分析
RT△的判定,通常有三種方法:①直接證明一個內角是直角;②證明兩銳角互余;③證明三邊滿足a2+b2=c2,也就是應用勾股定理逆定理。本題題干中沒有線段長度的條件,故無法考慮第三種方法。
解法1:因為△ABD是由△ABC翻折而來,故△ABD ≌△ABC,可得∠ABD =∠ABC=90°。又B、E、F、D內接于圓,利用“圓內接四邊形對角互補”可得∠BEF=90°。
解法2:得到∠ABD =∠ABC=90°后,利用圓周角推論可得BF是直徑,再利用“直徑所對圓周角是直角”得到∠BEF=90°。
解法3:得到∠ABD =90°后,將它分成兩個角∠FDE和∠BDE,再利用“同弧所對圓周角相等”,將這兩個角分別等量代換到∠FBE和∠EFB,得到∠FBE+∠EFB=90°,利用兩銳角互余的三角形是直角三角形得證。
簡析:顯然,運用解法3的同學對教材中圓內接四邊形的基本圖形不夠熟悉,但是能進行正確的等量代換,說明其還是具備了一定的幾何素養。
(二)第(2)題的解法分析
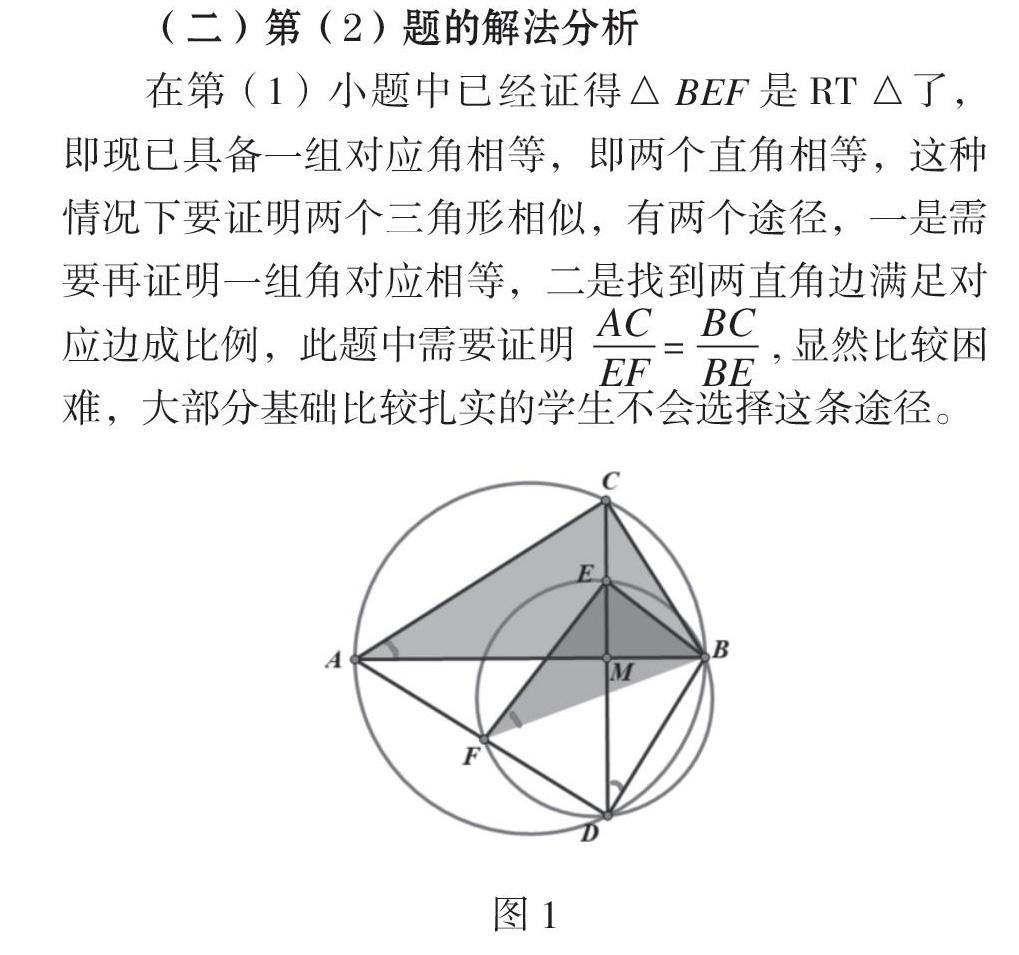
在第(1)小題中已經證得△BEF是RT△了,即現已具備一組對應角相等,即兩個直角相等,這種情況下要證明兩個三角形相似,有兩個途徑,一是需要再證明一組角對應相等,二是找到兩直角邊滿足對應邊成比例,此題中需要證明? ? ? ? =? ? ? ? ,顯然比較困難,大部分基礎比較扎實的學生不會選擇這條途徑。
解法1:如圖1,由(1)得知∠ABD =∠ABC =90°,可得A、C、B、D四點共圓,故∠CAB =∠CDB(或∠CBA =∠CDA),又B、E、F、D內接于圓,可得∠EFB =∠CDB(或∠EBF = ∠EDF),∴∠CAB=∠EFB(或∠CBA =∠EBF).
解法2:如圖2,∠ACB=90°,CD關于AB軸對稱,故CD⊥AB,可以發現母子相似的基本圖形,利用同角的余角相等,可得∠CAB=∠1,再由軸對稱性可得∠1=∠2,又B、E、F、D內接于圓,可得∠EFB =∠2,∴∠CAB=∠EFB。
或者要證∠CBA =∠EBF也是同樣的。
簡析:解法1用了兩次等量代換,顯然較為快捷,且學生能使用四點共圓,必定平時的學習是有拓展思維的。解法2用了三次等量代換,次數要多一次,但是用解法2的同學觀察到了“母子相似”這一基本圖形,這一基本圖形可以幫助我們通過“射影定理”得到很多的線段的數量關系,很多的角的數量關系,對第(3)小題的解決會起到一定的作用。
(三)第(3)題的解法分析
這一小題的解法是最多的,但是繞不開建模的思想,也就是根據線段的數量關系建立方程,一般幾何中可以找到的等量關系就是相似三角形對應邊成比例,以及直角三角形的勾股定理。
1.思路1:相似與勾股結合,利用射影定理或者勾股定理將線段表示成關于m的代數式,最后根據相似三角形對應邊成比例或勾股定理建立方程。
幾何題中求線段長度最常用的基本方法是根據三種關系列等式:勾股,相似,等積。在本題中顯然等積法的計算量過大,不具有優勢,但是并非不可以。這個方法雖然繁復,但是可以將幾何中計算線段的基本方法在此題的解法中補充完整。其實,此題中有非常多的直角三角形,所以線段之間的數量關系也可以用三角函數去表示;另外,本題的相似和勾股非常多,多種組合均可列出更多方程或方程組,筆者這里就不再一一列舉了。
所謂一題多解,多解歸一,最終劃歸為根據數量關系建立方程模型,因此通過此類幾何題能夠檢驗出學生的劃歸能力和建模能力的水平,能夠衡量出學生的數學素養。
四、從特殊到一般的試題拓展
此題是EF和AB互相平分,從而得到線段之間特殊的數量關系。如果我們將它一般化:
教師也可將原題中AB的長度改成其他數值,此時,解題思路和方法依舊不變。一則是希望學生能理解研究幾何的一般規律:一般到特殊,特殊到一般,以及理解動態問題中的不變的關系和量。另一則也是希望學生能領悟代數問題中的數式通性。
五、教學導向分析與教學建議
楊樂院士在《現代數學發展及其對基礎教育的影響》中指出:“平面幾何這一人類歷史上非常重要的理論,我們還是應該很好地掌握,因為我覺得現在還沒有別的東西能代替平面幾何對中學生進行幾何直觀能力和邏輯推導能力的訓練。”
而多年來,浙江省內多地雖然采用不同版本教材,但是各地中考均堅持關注核心內容及其教學,關注考查核心素養,類似這樣的命題對幾何解題教學起到正面積極的導向作用。
本題雖然是圓背景下的幾何綜合題,但是轉化劃歸后,實際上是需要解決三角形問題,因此在解題教學中,我們一定要引導學生在平時的解題過程中及時歸納總結基本圖形,并熟悉基本圖形,包括熟悉圖形的特征及基本元素之間的位置關系和數量關系。學會在復雜的圖形中分離出一些基本圖形,將復雜的問題轉化為我們熟悉的問題。
要能發揮好“基本圖形”的作用,實質上是要幫助學生在研究平面幾何的過程中學會思考,提高發現和提出問題、分析和解決問題的能力,這是能力和素養的標志。
而要發揮“基本圖形”的力量,解題教學的設計可以先“基本圖形”,再“變式圖形”,最后“綜合圖形”,讓學生在連續有關聯的幾何問題解決中得到邏輯推理論證的技能訓練,學會靈活運用概念、性質解決平面幾何問題。
教師要引導學生明確基本圖形的條件和適用情形,在推理過程中必須每一步都論據充分,用歸納、演繹進行推理,避免出現胡亂套用,或者邏輯不清的情況。此外,切忌拿“基本圖形”的結論作為定理使用,我們要用嚴密性、準確性和明確性作為邏輯推理能力的衡量標準。
參考文獻:
[1]易良斌.中學數學教與學研究與引領[M].北京:光明日報出版社,2015.
[2]章建躍.數學教育隨想錄[M].杭州:浙江教育出版社,2017.
[3]章建躍.立體幾何教學中的幾個問題[J].中學數學月刊,2015(10).
(責任編輯:奚春皓)

