基于核心素養培育需要的初中數學課堂興趣激發

王朝暉

[摘? 要] 基于核心素養培育的需要，去實現初中數學課堂上學生學習興趣的激發，是一個新的研究話題. 全國著名數學教育專家呂傳漢教授曾經提出了教體驗、教思考、教表達的“三教”理念，在初中數學課堂上要真正實現“三教”，就必須真正以學生為研究對象，要讓學生在自身興趣的驅動之下，高效地進行數學知識的建構，從而為核心素養的培育奠定基礎.

[關鍵詞] 初中數學;核心素養;核心素養培育;興趣激發

在初中數學教學中，培養學生的學習興趣是一個傳統的話題，對于課堂學習興趣的激發，可以從兩個角度來理解：從非智力因素的角度來看，興趣的培養實際上就是讓學生對數學學習有內在的驅動力，要讓學生對數學學習具有明顯的心理傾向，從這個角度來看，學生課堂興趣的激發，在于挖掘數學自身的魅力，以讓學生對數學及數學學習產生興趣;從學習目標達成的角度來看，興趣是達成學習目標的基礎. 當前對教學目標的達成，最新的描述是核心素養，而學生核心素養的培養，最終要落在學科核心素養的培育上，要將學生核心素養的培育有效融入數學教與學的過程中，落實到每一位學生身上，就需要結合具體的教學實踐過程去進行. 很顯然，這樣一個實踐過程需要以興趣作為基礎. 如果說前一個角度是初中數學教學的傳統研究視角，那基于核心素養培育的需要，去實現初中數學課堂上學生學習興趣的激發，就是一個新的研究話題，本文試對此展開闡述.

初中數學教學中的興趣激發應有核心素養指向

強調在初中數學教學中，興趣的激發應該有核心素養指向，這實際上是將初中數學教學的傳統與當下核心素養及其培育需要結合起來的產物. 又或者說，對于學生而言，這是一個學習起點與學習目標之間的關系，只有學生從數學學習的興趣出發，才有可能最終到達核心素養落地的彼岸. 對此筆者有這樣幾點理解：

一是當學生對數學學習有了內在的興趣之后，學生可以更好地實現對生活事物的數學抽象.

數學抽象是數學學習的第一步，尤其是對于初中數學而言，能否有效地進行數學抽象，很大程度上決定了數學知識尤其是數學概念學習的質量. 數學抽象本身是一個較為繁雜的過程，具有一定的挑戰性，如果沒有明顯的興趣驅動，那數學抽象是很難完整地完成的.

二是當學生有了內在的興趣驅動之后，學生可以對數學關系進行更好的邏輯推理.

數學是一門邏輯的科學，離開了邏輯，數學知識的大廈就無法真正建構起來，當日常的初中數學教學強調通過“因為”“所以”來完成問題解決時，實際上就是在運用邏輯關系，而對于相當一部分初中學生來說，邏輯推理是一個枯燥的過程，只有有了內在的興趣驅動，邏輯推理的過程才有可能持續高效地完成.

三是當學生對數學學習有了持久的興趣之后，學生可以更好地進行數學建模.

數學建模在數學學科核心素養體系當中，可以說具有承上啟下的作用. 在初中數學知識體系當中，有著相當多的或隱或現、大小程度不同的數學建模過程，相對于邏輯推理而言，數學建模更加抽象，更加繁雜，因此更加需要興趣驅動，而且這種興趣必須是持久的興趣.

由此可見，核心素養背景下的初中數學課堂上，興趣的激發絕對是一門學問，甚至可以認為是一種課堂文化.

核心素養下初中生數學興趣激發的文化內涵

之所以認為數學課堂上興趣的激發是一種文化，是因為數學課堂文化是凝聚著數學傳統和師生主體間性色彩的課堂，而數學文化是構建數學課堂文化的一個重要理論來源. 其實這也是相對于教師而言的，教師的教學研究需要一種文化氛圍，需要文化驅動，只有將教學研究視作一種文化時，教學研究才能彰顯出其推動教學進一步發展的價值. 在初中數學教學研究的視野里，教師是影響初中生數學學習興趣最為重要的因素. 因此作為興趣激發的主體，教師立于學生的數學學習興趣與核心素養之間，起著無可替代的作用.

以“線段的軸對稱性”教學為例，從知識的角度來看，這是一個非常抽象的知識，因此如果直接教學這部分知識，學生是不大感興趣的. 但是這個知識又蘊含著豐富的核心素養元素，如果學生沒有高效地參與，那這些營養元素就會流失. 基于這樣的考慮，筆者進行了如下的教學設計：

首先，為學生設計一個體驗活動. 讓學生在一張紙上畫出一條線段，然后通過折疊的方法，讓線段的兩個端點A和B重合，完成這個體驗活動之后讓學生去尋找發現. 還可以進一步設計這樣一個體驗活動：在上一步的基礎上，到折痕中任意取一點記作P，然后連接PA和PB，再沿著折痕重新折疊，看看有什么樣的發現.

通過這樣一個體驗活動，首先可以激發學生參與的興趣，學生經過折疊的體驗，去鞏固已有的對稱性認識;再通過熟悉體驗基礎上的陌生體驗，進而有了新的發現，這個發現可以為后面知識的學習奠定基礎.

其次，為學生設計一個邏輯推理活動. 其實好多同學通過上述體驗過程，就能夠提出問題，提得最多的問題就是：為什么到折痕中任意取一點記作P，然后連接PA和PB，沿著折痕重新折疊后，PA會和PB重疊呢？這是偶然的還是必然的？

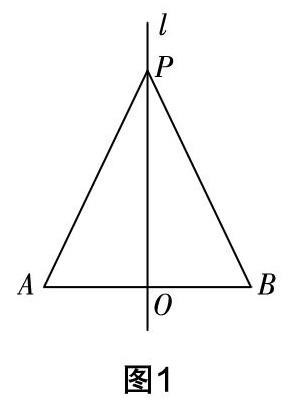
有了這樣一個問題的驅動，學生也就有了探究的興趣，相對于體驗活動中的興趣而言，此時的興趣層次更高，指向數學探究的興趣. 而數學探究是離不開邏輯推理的，所以在這個教學環節，不妨再讓學生在體驗過程中形成的認識的基礎上，去進行自證. 實際上就有學生發現了“任何一個線段都是軸對稱圖形，而線段的垂直平分線就是它的對稱軸”“線段垂直平分線上的點到線段兩端的距離相等”，但是這些發現是通過折疊得到的，它們是否能夠得到證明呢？這是許多學生關心的話題——學生關心也就意味著興趣的存在，所以這個時候好多學生都會將自己的認識改編為一道證明題：如圖1，已知l是線段AB的垂直平分線，求證PA=PB. 具體的證明過程限于篇幅，這里不再贅述. 但是這樣一個證明過程肯定是與邏輯密切相關的，興趣驅動了學生進行邏輯推理，又通過邏輯推理進一步驗證了自己的猜想，于是邏輯推理這一核心素養要素就得到了充分的培養.

特別值得一提的是，由于此處學生已經進行了充分的邏輯推理，因此學生在后面研究“角的軸對稱性”的時候，顯得更加輕車熟路.

再次，用數學建模的過程為學生建構線段的軸對稱性認識.

傳統的教學過程中，教師只是讓學生記住現成的結論，而在核心素養的視角之下，筆者建議將這一過程設計為一個數學建模的過程. 可以說每一個數學結論都是模型認知，因此記住結論就是幫學生建立模型，只有這些模型生動形象，學生在利用它們解決問題的時候才能得心應手.

基于數學學科核心素養的本質

理解興趣的激發

在核心素養的視角之下，思考初中數學教學中的課堂興趣激發這樣一個最基本的問題，筆者以為是十分有意義的，無論是對教師的教來說，還是對學生的學來說，其意義不僅在于能夠讓學生在課堂上帶著更濃厚的興趣去學習，也為數學教師教學水平的提升帶來契機. 全國著名數學教育專家呂傳漢教授曾經提出了教體驗、教思考、教表達的“三教”理念，其進一步指出，教體驗從本質上說就是讓學生會用數學的眼光觀察現實世界，而這就是提醒數學教師要注重數學抽象和直觀想象核心素養的培養;教思考從本質上說就是讓學生會用數學的思維分析現實世界，而這其實就是強調要注重邏輯推理和數學運算核心素養的培養;教表達從本質上說就是讓學生會用數學的語言表達現實世界，很顯然這就是注重數學建模和數據分析核心素養的培養.

在筆者看來，這樣一段論述是對數學學科核心素養最好的闡釋，而在初中數學課堂上要真正實現“三教”，就必須真正以學生為研究對象，要讓學生在自身興趣的驅動之下，高效地進行數學知識的建構，從而為核心素養的培育奠定基礎.

總之，數學課堂上興趣的激發這樣一個傳統的問題，需要置于核心素養的視角下來解析，這樣才可以更好地用興趣驅動學生數學學科核心素養的落地.