把課堂交給學生 把學生推到臺前

孫群安

摘要：文章從兩個等差數(shù)列的問題教學入手，全過程體現(xiàn)了學生的主體性，解題思路的講解、思維方法的歸納、小結和點評最終都由學生完成，教師只在課堂推進過程中出現(xiàn)問題時，以及在每一轉(zhuǎn)換環(huán)節(jié)才適當加以引導。課例通過科學、細致的學情分析，合理的課堂組織，努力培養(yǎng)學生的數(shù)學思維能力。

關鍵詞：學情分析；主體性；數(shù)學思想；自主探究

一、教學過程點評

在本節(jié)課前，教師進行了一個檢測，主要考查等差數(shù)列的教師教學與學生學習效果，共兩道解答題。本節(jié)課教師準備就檢測題的解題思路進行分析，采用學生自主探究的形式。

在大多數(shù)情況下，課堂導入是課堂開始吸引學生注意力、引導學生思考的重要環(huán)節(jié)。本節(jié)課是一節(jié)習題講評課，因此課堂導入非常簡單，直奔主題，課堂

導入根據(jù)課堂需要進行了靈活處理。

師：同學們聽懂了嗎？

生：沒有。

師：為什么？

生：條理和邏輯不清晰。

【點評】數(shù)學表達能力是學生學習數(shù)學的目標之一，也是學生數(shù)學思維形成的有效方式之一。生1的數(shù)學表達所反映的問題給教師提供了很好的素材，使生1對照自己總結經(jīng)驗，學會反省，達到自我優(yōu)化的目的，其他學生從中吸取教訓，避免類似問題的出現(xiàn)。

2.對比示范，理解正確表達

師：那么怎樣才能做到條理和邏輯清晰呢？下面我們再讓一名學生介紹下自己的思路。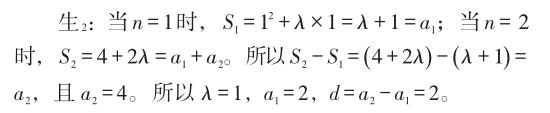

此時大部分學生表示已經(jīng)理解了。

【點評】數(shù)學思想方法的教學需要較長時間的堅持才能有效，是潛移默化、潤物細無聲的“慢工”，體現(xiàn)在不斷變化的課堂進行中。本節(jié)課通過兩名學生不同解題思路的分析、對比，學生掌握了此題的解題思路，知道了如何用正確的數(shù)學方式去表達，也體會到了清晰的數(shù)學表達的好處。

3.引導學生小結，促進思維形成

師：請同學們想一想，解決這道題的關鍵是什么？

學生思考，沉默。

師：這道題的已知條件涉及了哪些知識？

生3：有等差數(shù)列、等差數(shù)列的項、等差數(shù)列的前n項和，等等。

師：所以這道題的解題關鍵是要建立什么關系？

生3：關鍵在于建立等差數(shù)列的項與前n項和之間的關系。

師：哪名學生說一下等差數(shù)列的項與前n項和之間有哪些關系呢？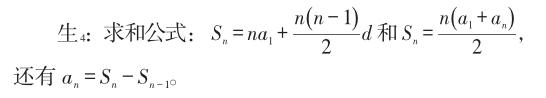

【點評】教師在課堂中是觀察者和引導者，在學生自主學習的過程中，觀察學生對數(shù)學知識和數(shù)學問題的理解情況，并設計恰當?shù)膯栴}，引導學生深入思考。

這道題學生通過等差數(shù)列的項與前n項和之間的關系，分析找到了解題的突破口，在教師的引導下，總結出一類問題的解題思路，實現(xiàn)了數(shù)學思維的形成。

4.練習提高，檢驗探究成果

師：非常好！下面我們來看下一道題。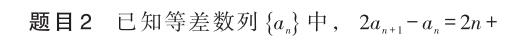

【點評】在教師細心、及時的引導下，學生開始注意數(shù)學表達的清晰、準確，從而提高了學生自主學習的效率。

5.及時階段小結，形成數(shù)學思維

師：這個解法的數(shù)學思維方法的特點是什么？生：代數(shù)運算。

師：除了代數(shù)運算，生5通過取n=1和n=2兩種特殊情況求通項公式an，體現(xiàn)了什么數(shù)學思想？

生：從特殊到一般。

【點評】學生自主學習探究過程中的提煉、總結，可以逐步幫助學生提高數(shù)學學科核心素養(yǎng)，最終達到鞏固和升華。在這個環(huán)節(jié)中，教師的引導作用得到凸顯。

6.開拓解題思路，激發(fā)學習興趣

師：同學們還有沒有其他解法？

【點評】一題多解可以開拓學生思路，激發(fā)學生興趣，是很好的培養(yǎng)學生創(chuàng)新思維的方法。本節(jié)課特別注重對學生思維的開發(fā)，鼓勵學生不同思維的碰撞。

7.反思思維過程，鞏固數(shù)學思想

師：這個解法的思維方法的特點是什么？

生7：運用了等差數(shù)列an+1與an這種前后項之間的關系，即an+1-an=d。

師：這就是遞推關系的本質(zhì)，還有呢？

學生沉默思考。

生8：函數(shù)思想。

師：對，函數(shù)思想是一種重要的數(shù)學思想。

【點評】課堂小結不僅是課堂結束后做的事情，每一個教學環(huán)節(jié)結束后的思維過程的反思也更有針對性。

8.拓展學生思維，培養(yǎng)創(chuàng)新意識

師：大家想想，還有什么方法可以解決這個問題？

學生討論，但是沒有結果。

【點評】本節(jié)課兩道題的解答思路都不唯一，體現(xiàn)了教師設計問題的深思熟慮，以及科學性和嚴謹性，讓學生對每道問題從不同方面進行解讀和思考，不僅可以收到同樣的效果，還幫助學生避免陷入題海戰(zhàn)術的陷阱，使學生的思維得到拓展，創(chuàng)新意識逐步形成。

二、教學亮點分析

1.科學、細致地學情分析

本節(jié)課從兩道等差數(shù)列的問題入手，全過程體現(xiàn)了學生的主體性，解題思路的講解、思維方法的歸納、小結和點評都由學生完成，教師只在課堂推進過程中出現(xiàn)問題時，以及在每一次轉(zhuǎn)換環(huán)節(jié)才加以引導。

著名作家、演說家肯·羅賓遜說過，人的潛能猶如礦產(chǎn)資源，埋得很深。由此可見，教師對學生有充分的信任，開展學生自主探究學習，最大的困難在于課堂節(jié)奏的控制，課堂效率的掌握，這都要求教師對學生非常了解。對學生自主學習過程中可能出現(xiàn)的問題有一個基本的判斷，整節(jié)課教師看似參與很少，實際上教師對課堂的進程和節(jié)奏胸有成竹。教師的自信來自對學生學情的充分分析與準確把握。

2.合理利用課堂教學中出現(xiàn)的狀況

數(shù)學教學需要教學理論的支撐和經(jīng)驗的積累，需要逐步提升教學應變能力，合理利用教學過程中出現(xiàn)的任何狀況，把它變成我們的教學資源和教學契機。

本節(jié)課在第一道題生1的回答中出現(xiàn)了一些情況，這并不是事先設計出來的，如果教師能有效利用，對教學來說并不一定是壞事，與經(jīng)過事先設計的正確的解題示范相比，效果會更好。本節(jié)課教師把握住了教學機會，加以利用這一情況，很好地促進了教學目標的達成。在教學過程中，常常會有許多意想不到的事情發(fā)生，有經(jīng)驗的教師反而會借力打力。

3.充分發(fā)揮學生的主體性

本節(jié)課充分發(fā)揮了學生的主體性，所有問題的解決要么是學生獨立思考，要么是合作討論得出，在必要的環(huán)節(jié)和內(nèi)容轉(zhuǎn)換時教師才適時出現(xiàn)。在整個過程中，教師以觀察為主，引導時機把握得恰到好處，有效培養(yǎng)了學生的數(shù)學學科核心素養(yǎng)，為學生的可持續(xù)發(fā)展和終身學習創(chuàng)造了條件。

教師更多的時候是觀察者和引導者。在學生自主學習的過程中，觀察學生對數(shù)學知識和數(shù)學問題的理解情況，并設計恰當?shù)膯栴}，引導學生深入思考，實時小結，開展合作學習等，根據(jù)學生的發(fā)展情況，構建基于核心素養(yǎng)的各種活動。例如，在學生出現(xiàn)數(shù)學表達問題時，教師并沒有直接給出，而是引導學生說出；在學生不能直接總結出題目1解題的思維關鍵時，教師立刻設置一個臺階，引導學生發(fā)現(xiàn)問題的答案。在學生沒有發(fā)現(xiàn)2an+1=an+an+2對題目2的解題思路的幫助時，教師設計問題，引導學生去發(fā)現(xiàn)。

4.注重學生數(shù)學思想方法的形成

學生數(shù)學思想方法的形成是一個漸進的過程，考驗著教師的耐心和毅力，它蘊藏在數(shù)學的每一個細節(jié)中，都需要較長時間的堅持才能奏效。數(shù)學學習不僅是解數(shù)學題，而是通過解決數(shù)學問題，幫助學生領會數(shù)學思想方法，每一個思維過程的小結都是一個非常好的幫助學生提升數(shù)學學習能力、培養(yǎng)數(shù)學思維的手段。本節(jié)課通過學生解決兩道數(shù)學問題的步步推進，特別注意在課堂上滲透、提煉與概括。例如，通過解答題目2的第一種解法的解題思路分析，了解了從特殊到一般的數(shù)學思想方法，通過解答題目2的第二種解法的解題思路分析，了解了函數(shù)思想在數(shù)列的應用，在不斷變化的課堂進程中，幫助學生逐步掌握數(shù)學思想方法。數(shù)學思想是靈活運用數(shù)學知識解決問題的支撐。

本節(jié)課教師努力創(chuàng)造學生自主學習的氛圍，真正做到了把課堂交給學生，把學生推到前臺，通過師生之間問題的探討、思想的碰撞、情感的交融，達到學生的共同成長和個性發(fā)展，避免出現(xiàn)一切完全都是在教師控制之下虛假的“自主”學習。

參考文獻：

[1]萬軍.高中數(shù)學教學引導自主探究學習“三策略”[J].數(shù)學教學通訊，2019（18）.

[2]李亞珍.分析高中數(shù)學課堂中探究性學習的困惑與思考[J].課程教育研究，2018（50）.

[3]李桂紅.試論高中數(shù)學教學中的自主探究學習[J].數(shù)學學習與研究，2017（16）.