初中數學開放題的教學策略分析
徐樂華
摘要:隨著教學改革的不斷深化,追求解題方法的多樣性,積極培養學生的創新思維,越來越受到師生的重視。當前,開放題普遍成為各地升學考試中的必考題目。因此,探究開放題的教學價值顯得十分重要,本文就初中數學開放題的教學策略進行了分析。
關鍵詞:初中數學;開放題;教學價值;教學策略
中圖分類號:G633.6文獻標識碼:A文章編號:1992- 7711(2020) 06-0017
初中數學作為一門基礎性較強的必修類科目,其教學目標不僅在于讓學生掌握對應的文化知識,還應通過數學學習,在一定程度上提升學生的核心素養。開放題目的設置,對于培養學生的創新性思維是非常有幫助的。
一、選題難度要適當,提升學生做題興趣
初中數學設置開放題的意義在于可以讓學生按照自己喜歡的方式去做題,大多數開放題是沒有固定答案的,解題方法也有很多種,甚至有的題目里給出的條件都是可以根據學生的知識掌握水平進行取舍的。
開放題的選擇要考慮到很多因素,比如學生的接受程度、教師的講課進度、課程的內容等。比如,當教師講到八年級上冊《全等三角形》這一課時,可以針對全等三角形的定義、性質、特點和全等三角形必須滿足的條件等基礎知識,給學生留一個這樣的開放題型:“兩個三角形兩個邊和一個角對應相等的三角形不一定全等,為什么呢?”教師可以引導學生一起去探究,準備A4紙若干、三角板若干、鉛筆若干、橡皮擦幾塊,讓學生畫出滿足以上條件——兩個邊和一個角相等的三角形,在畫的過程中他們就會發現只有當相等的那個角是夾角時這兩個三角形才會全等,否則各種情況都有可能。假設兩個相等的邊是a、b,另一條不確定邊長的邊是c,以邊a和邊b的交點為圓心,邊a和邊b的長度為半徑畫弧線,改變邊a和邊b的長度就會發現弧線和邊c的交點有可能有一個,有可能有兩個,也有可能沒有交點。當只有一個的時候,這個三角形就是斜邊的直角三角形,直角對應的邊是邊b。知道以這種方法畫圖的學生并不多,教師在看到學生遇到問題的時候可以適當提醒,引導學生往圓這個方向去思考,然后讓學生自己動手去畫,在畫的過程中他們自己就會找到答案。像這樣的題目完全是概念型的問題,只要認真聽課每個學生都可以回答上來,平時學習不好的學生教師稍微提點一下也能找到答案,如此學生的自我認同感才會提高,隨之而來的學習積極性也會大大提升。
二、解題過程中注重學生之間的交流,培養學生合作學習習慣
設置數學開放題就是為了打破傳統的學生課后刷題、復習的單一僵化的學習模式,初中數學知識說難不難說易不易,按照傳統的教學模式讓學生掌握知識點是完全沒問題的,但是卻不利于學生長遠的發展規劃。
教師在課堂上讓學生以小組形式完成開放習題時,一定要維護好課堂秩序,監督學生學習,以防學生之間產生矛盾,萬一學生在某些觀點上出現分期,也要做好調解。有這樣一道開放題,題目內容是:“有一個小區搞綠化,想要在一塊長方形的空地上建一個花壇,要求設計的圖案由圓和正方形組成(圓和正方形的個數不限)并且使整個矩形場地成軸對稱圖形。”這個設計方案同樣有非常多種,教師可以給每一個小組準備一塊較大的硬紙板、鉛筆若干支、圓規一副、三角尺一副,讓學生畫出自己小組的方案。在開始畫設計圖之前教師可以為學生提煉出問題的主旨,如空地是長方形、用到的元素是正方形和圓,要求成軸對稱圖形。給學生提出這個,是為了避免學生設計的時候跑題。該題常見的兩種設計就是以下兩種方案。方案一:在長方形的正中間放一個圓形花壇,在長方形的四角分別放一個正方形的花壇;方案二:在長方形的正中間放一個正方形的花壇,正方形的兩邊放圓形花壇,然后在長方形的四角分別放一個正方形的花壇,這兩種方法的效果圖如下。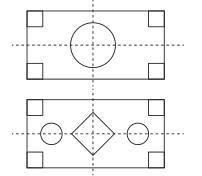
像這種有很多答案的題目,一個人的想法是有限的,無法顧及全局,有時想到一套方案,畫出來可能就不行,自己很難想出完善的辦法,而通過小組討論集思廣益就可以很快想出解決方案。在討論的過程中,學生可以毫無顧忌的發表自己的看法,可以讓學生的思維變得更加活躍,教師也可以在學生自主意識和探索精神方面加以引導。
三、解題結束后,教師引導學生針對解題思路進行復盤
從初中開始所有的數學題型都可以進行分類,而一個類別下的題目解題思路都是一樣的,所謂“萬變不離其宗”就是這個道理。每做完一道數學題,特別是像一些數學開放題一樣比較復雜的題目,對解題思路進行復盤是非常重要的一個流程。
例如,江堤邊一注地發生了管涌,江水不斷地涌出,假定每分鐘涌出的水量相等,若用2臺抽水機抽水,則40分鐘可抽完;若用4臺抽水機抽水,則16分鐘可抽完。如果要在10分鐘內抽完水,那么至少需要抽水機幾臺?江水的流動量是不可測的,為了讓學生更好的理解這一道題,建議教師將不可測量的江水變成可視化的實驗。教師可以準備3個大箱子,一個大箱子里放滿小塑料球,一個箱子里是空的,讓學生每分鐘拿出一定數量的小球放進另一個箱子里,模擬江水涌出的過程,再讓2個學生模擬抽水機在一定時間內拿出小球到第三個箱子里,按照此類方法進行接下來的實驗,題中給出的時間太長不好模擬,建議同比壓縮時間,得出了結論在同比擴大就是問題的答案,改變拿出小球的時間和數量總結出規律。在實驗結束后,教師可以和學生一起對題目進行復盤,總結出常規做題的方法——設而不求法,相信經過教師組織的實驗和師生對解題思路共同復盤的過程,學生下次遇到像這種變化型的題目定能迎刃而解。
綜上所述,教師可在解題結束后,引導學生針對解題思路進行復盤,解題過程中注重學生之間的交流,培養學生合作學習習慣等措施。
(作者單位:浙江省樂清市大荊鎮第一中學325600)

