用沖突引領學生自主建構數學概念
【摘要】本文以人教版教材《用數對確定位置》教學實踐為例,論述在小學數學教學過程中以沖突引領學生自主建構概念的策略,提出激活生活經驗引發認知沖突、創設探究情境制造認知沖突、誘發應用爭議直面認知沖突等教學建議。
【關鍵詞】認知沖突 自主探究 概念建構
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2020)37-0101-02
學生并不是一張白紙,他們在生活實踐中形成了一定的認知結構,但這種認知結構和面臨的學習情境之間存在著一定的差距,這種差距會導致已有知識、已有經驗與新知之間的失衡。這種暫時的失衡和矛盾被稱為認知沖突。如何利用認知沖突,幫助學生從模糊走向清晰,從混沌走向通透呢?筆者以《用數對確定位置》一課為例,談四點體會和思考。
《用數對確定位置》是人教版教材六年級下冊的內容。學生在一年級已經學會用直線上的點描述數的順序和大小關系,也積累了用類似第幾排第幾個描述物體位置的方法。根據教材內容以及學情,筆者將教學重點放在讓學生掌握運用數對確定位置的適用范圍,并理解和掌握其中蘊含的數學規則上。也就是說,要讓學生在新舊經驗的沖突中自主探究、自主思考,使認知結構完成一次重組和優化,從而逐步將日常經驗上升到抽象的經驗,深入理解和內化“用數對來確定位置”這一數學概念。
一、激活生活經驗,引發認知沖突
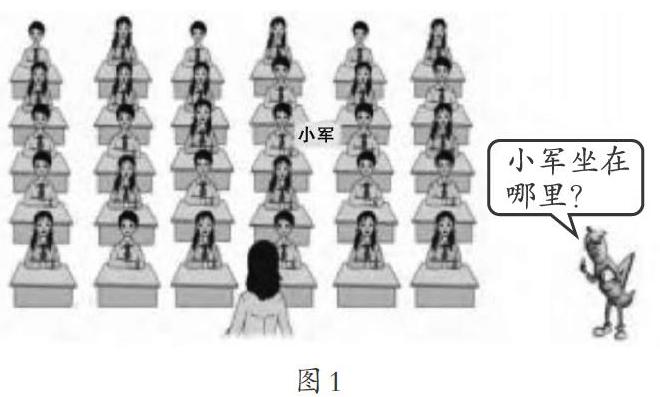
筆者出示主題圖(如圖1),引導學生進行思考:
①遮蔽其他豎排,只剩下小軍這一豎排。找出小軍坐在哪里?學生認為小軍在從前數第3個,從后數第3個。
②遮蔽其他橫排,只顯示小軍這一橫排。找出小軍坐在哪里?學生認為小軍在從左數第4個,從右數第3個。
③出示完整座位圖。請找出小軍坐在哪里?針對這一問題,學生的說法不一,有的認為在第3排第4個,有的認為在第4組第3排,有的認為在第3組第3排,有的認為在第3組第3個。
④筆者追問:“假如沒有座位圖,只根據大家說出的位置,能確定這是同一個位置嗎?”學生認為不能。由此引發認知沖突。筆者繼續追問:“由于標準不統一,每個人的說法不一樣,描述的位置就沒有確定性,如何解決這個問題呢?”學生認為要把觀察的方向用同一個標準規定。此時,筆者出示規則:豎排叫做列,橫排叫做行。確定第幾列要從左往右數,確定第幾行要從前往后數。
⑤請用行和列說出小軍的位置。學生找出在第4列第3行。
【教學思考】學生在一年級已經有了用直線上的點描述數的順序和大小關系的經驗,在生活中也能夠運用第幾排第幾個的方式描述物體的位置。筆者給學生呈現了教室里有序排列的座位場景,激活學生的已有經驗,讓學生在多種描述位置的方法中選擇一種精準的描述方法。這與學生已有的認知結構產生了暫時性的矛盾沖突。在這一矛盾的指引下,學生展開了自主思考,提出要建立統一的標準和規則,由此,學生原有的認知結構中對位置的模糊表達,在認知沖突的推動下,漸漸向著統一標準下的精準數學表達這個方向邁進。
二、創設探究情境,制造認知沖突
筆者創設了一個“你說我寫”的游戲情境:讓一部分學生依次說出屏幕上指定的位置,另一部分學生把答案記錄在紙上。引導學生展開探究:
①想一想,這樣的記錄方法簡便嗎?(學生認為比較麻煩)由此提出想用一種簡單的寫法代替第幾行第幾列。
②筆者讓學生分組以小軍的座位第4列第3行為例,用自己的方法寫出這個位置。學生的寫法不一,有的用“4列3行”表示,有的用“4 3”表示,有的用“L4R3”表示……筆者引導學生分析,找出每個小組不同寫法中的共性。學生發現,不管用哪一種寫法,這里的4都表示第4列,3都表示第3行。
③筆者引出數對概念,板書(4,3),讓學生說出數對中4和3分別表示什么意思?
④筆者讓學生繼續游戲。一組同學說出位置,另一組同學用數據記錄。
【教學思考】學生初步建立了用行和列來確定位置的數對認知,還需要自主探索如何進行快速科學的數對讀寫。筆者并沒有簡單告知學生這一教學關鍵點,而是創設“你說我寫”的游戲情境,讓學生直觀感知記錄數對的麻煩,再次引發認知沖突,帶領學生展開探究,去尋找一種簡潔明了的記錄方法。為此,筆者讓學生充分參與知識的建構,主動嘗試創造自己的寫法,并在不同的方法中尋找共同的屬性,數對的概念和特征呼之欲出。通過這樣自主體驗的過程,學生會將實際問題抽象成數學模型,在深入理解數對的同時也體會到數學的簡潔之美。
三、誘發應用爭議,直面認知沖突
筆者讓學生使用數對表示班級中劉[××同學]的位置,學生產生了爭議。有的從右往左數,認為是(4,1),有的從左往右數,認為是(5,1)。為什么會出現兩種不同的表示方法呢?到底哪一種才是正確的呢?筆者引導學生展開討論,發現問題爭論的焦點是如何確定班級中的第1列。筆者在大屏幕出示班級座位全景圖,讓學生統一從左邊數起,確定第1列。學生認識到,為了把空間里的位置和平面圖上的位置進行統一觀察,就要從觀察者的左邊數起,確定第1列,也就是說,班級中座位的第1列要從站在講臺前觀察者的左邊數起。由此學生找到了劉[××]的位置是(5,1)。最后,筆者讓學生用數對確定自己的位置,在紙上寫下來,并歸納總結:在觀察空間里的位置時,都要從觀察者的左邊數起,確定第1列。
【教學思考】學生學會了用數對確定平面圖上的位置后,就需要應用數對確定教室里的位置。根據現實經驗,大部分學生在確定現實空間中的第1列時,會和平面圖形中的第1列產生混淆,導致出錯。為此,筆者直接將這一爭議性的問題拋出來,誘發學生辯論。學生在思維的碰撞下展開質疑和辯論,經過探究思考,他們認識到每個人的座位都是唯一的,表示位置的數對也是獨有的,數對與位置一一對應,由此自主建構了現實生活中用數對確定位置的科學方法。
四、拓展延伸,挖掘認知沖突
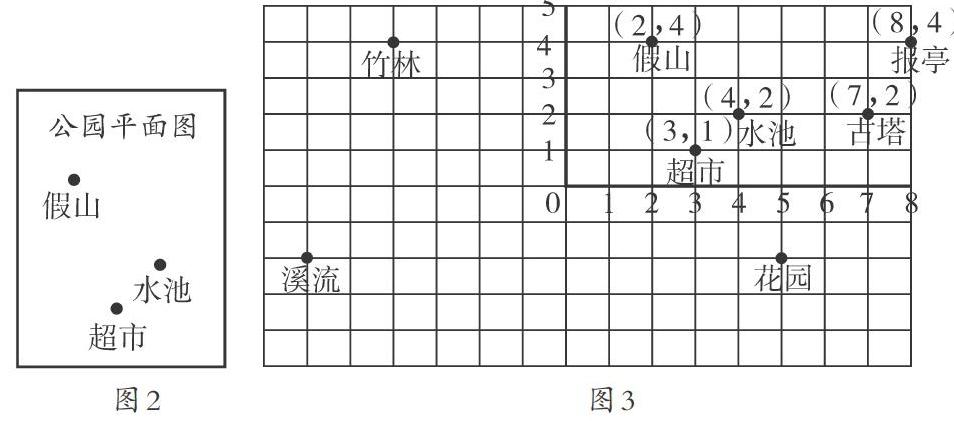
筆者給學生出示公園平面圖上的三個景點,要求學生確定景點的位置。(如圖2)學生認為,這三個景點在平面圖上沒有相關的數對數據,因此不能確定位置。此時,筆者給學生講述數學家笛卡爾受到蜘蛛織網的啟示,把蜘蛛看作一個點,蜘蛛的每個位置就能用行和列這一組數確定下來。學生受到啟發,認為可以在平面圖上列出網格,這樣就可以得出行和列的數據。接著,筆者給學生出示一張網格圖,并重新標注假山、水池、超市、古塔、報亭等景點的位置(如圖3),讓學生說出這些景點的位置。學生根據數對知識,分別列出假山(2,4),超市(3,1),水池(4,2),古塔(7,2),報亭(8,4)的位置。
最后筆者向學生揭示這就是笛卡爾坐標系,也是平面直角坐標系的雛形。筆者繼續追問:“想一想,花園、溪流、竹林的位置能確定出來嗎?”學生認為,花園,溪流、竹林在第幾行,第幾列沒有數據,因此不能確定位置在哪里。筆者告訴學生,這部分知識將會在初中階段進行系統學習,那時就會找到答案。
【教學思考】認知心理學認為,認知的螺旋是開放型的,它的開口會越來越大。在學生完成了學習目標,能夠運用數對表示具體情境中物體的位置時,筆者提出了新的問題,要求學生將散落的假山、水池、超市的位置用數對表示,這又引發了新的認知沖突。在這一認知失衡的驅動下,學生展開探究,將靜態的方格圖動態化,認識到行和列都可以延長移動,由此將知識拓展延伸,滲透平面直角坐標系的基本思想。
總之,在本次教學實踐中,筆者不斷打破學生思維中的平衡,運用一次次的認知沖突,引領學生經歷建構、重構的過程,由此獲得概念的自主建構,讓學生的認知結構不斷完善。
作者簡介:覃業蘭(1976— ),女,廣西玉林人,大學專科學歷,一級教師,主要從事小學數學教學與研究。

