GeoGebra軟件在中學物理教學中的應用探析
陳林 桑芝芳

摘? 要 借助GeoGebra軟件,通過繪制力的動態示意圖和相關函數圖像,深入探析一道動態平衡試題,糾正錯誤思維,突破傳統教學的局限性。
關鍵詞 GeoGebra;動態平衡;中學物理;現代教育技術
中圖分類號:G633.7? ? 文獻標識碼:B
文章編號:1671-489X(2020)13-0032-02
1 前言
掌握現代教育技術是每個新時代教師必備的技能。GeoGebra是一款優秀的動態數學軟件,在國外先后獲得多項教育獎項[1]。它的動態演示功能,可以將中學物理中很多抽象的、不易理解的內容形象、直觀、動態地展示,對學生的學習、教師的教學大有益處。
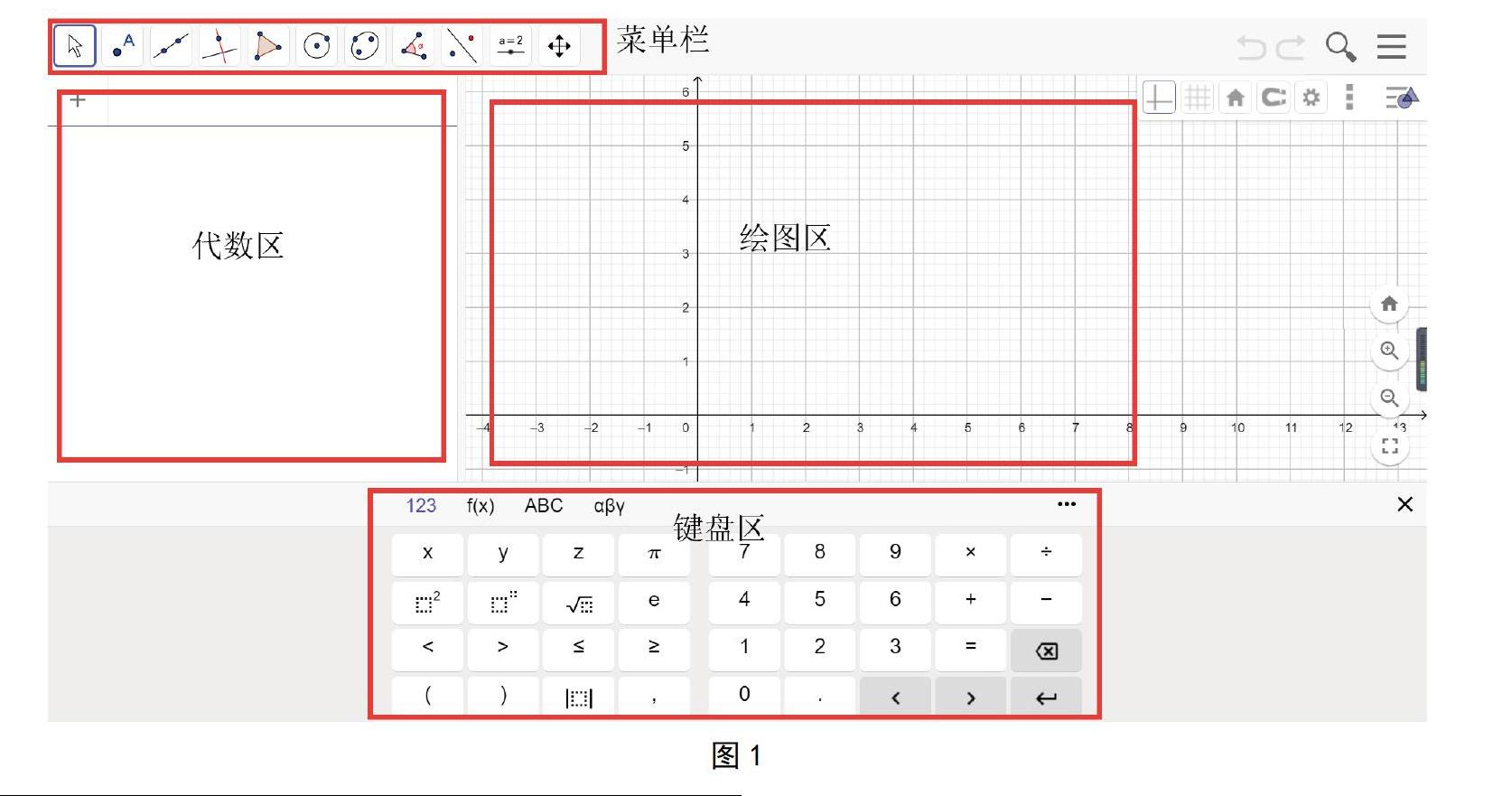
圖1所示是GeoGebra軟件的界面,菜單欄中包含大量工具,在代數區輸入函數,繪圖區就會出現對應的圖像。GeoGebra頁面簡潔,操作簡單,幾乎不需要編程基礎,包含了幾何畫板的所有功能,兼具Excel常用功能和Flash部分功能。值得一提的是,GeoGebra支持跨平臺使用,能在計算機、手機、平板、網頁上運行。本文接下來以一道動態平衡問題為例,借助GeoGebra軟件進行深入探討。
2 試題
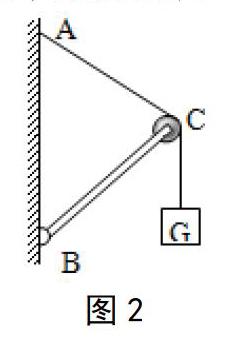
如圖2所示,桿BC的B端鉸接在豎直墻上,另一端C為一滑輪。重物G上系一繩經過滑輪固定于墻上A點處,桿恰好平衡。若將繩的A端沿墻向下移,再使之平衡(BC桿、滑輪、繩的質量及摩擦均不計),則(? ?)
A.繩的拉力增大,BC桿受壓力增大
B.繩的拉力不變,BC桿受壓力減小
C.繩的拉力不變,BC桿受壓力增大
D.繩的拉力不變,BC桿受壓力不變
3 問題解析
對C點進行受力分析,在GeoGebra中繪制出對應的受力示意圖,如圖3所示。當系統平衡時,繩的拉力始終等于重物的重力,即T1=T2=G,所以繩子的拉力T不變。
接著設繩AC與墻之間的夾角為θ,A端沿墻下移后再平衡時θ會變大。又因為圖中兩個三角形相似,所以T1與T2的夾角也變大,而T1和T2大小不變,所以FN增大,故選C。
4 題意的理解
上述解析采用相似三角形法看似簡單,但是筆者身邊的很多教師對其中的關鍵一步“再平衡時θ會變大”產生疑問:為什么就增大了呢?是顯然嗎?而且很多教師覺得是減小了,并畫出圖4。這是很多教師和學生心中的疑惑,但是物理是門講究依據的學科,接下來進行精確分析。
要想判斷∠BAC是變大還是變小,可以先確定∠ABC是如何變化的。若∠ABC在增大,因為△ABC是等腰三角形,則∠BAC在減小,反之則增大。
5 數學推導
不妨設∠ABC為α,如圖5所示,通過正弦定理可得:
a在減小,b/2a在增大,cosα增大,所以α減小,所以∠BAC增大。
因此,在A往下移的過程中,α減小,桿BC反而往上偏轉。很多教師或學生下意識地認為桿BC會往下偏轉,這便是錯誤原因所在。而且徒手畫的圖不夠精準,導致教師、學生陷入思維誤區。
6 GeoGebra驗證
在GeoGebra中繪制出題中示意圖,拖動圖6(a)中A點,發現A點在往下移動過程中,BC確實往上偏轉,如圖6(a)
(b)所示。而且通過右擊T1、T2、FN顯示它們的數值,可以清晰地看到在A往下移動的過程中,T1、T2、FN大小是如何變化的。
7 數形結合分析
在GeoGebra中往下移動A點的過程中發現,A移動到某處,桿BC會突然轉向豎直方向,此時BC與豎直方向還有較大的角度。多次實驗,依舊如此,應該是與a與α的函數關系有關。
先分析α和a的關系。由上述可知b/2a=cosα,得α=
arccosb/2a,b為定值,a為變量。可以利用GeoGebra畫出α和a的圖像,如圖7所示。發現隨著a的減小,α確實會突然減小到0。到這里,所有的疑惑完全解決。
8 GeoGebra操作步驟
繪制圖中示意圖? 在坐標系中,設(0,0)為B點,選取“線段”工具,過B點作定值線段BC。在y軸上取點A,選取“線段”工具,連接AC。選取“垂線”工具,過C點作x軸垂線,在垂線上選取點G。
繪制C點處受力示意圖? 在輸入欄輸入“circle(C,CG),交垂線于F,連接CF”。選取“平行線”工具,過F點分別作AC、BC的平行線,確定交點,隱藏不需要的對象。右擊重命名,將繩AC、CG和桿BC上的力分別命名為T1、T2、FN。受力示意圖的平行四邊形即可完成。
顯示力的大小? 右擊T1、T2、FN顯示“名稱和數值”,可以將力的大小顯示出來,而且在運動過程中會隨著運動的變化而變化。
9 結語
經過上述分析,對這道題有了更深入的理解。在日常教學中,教師和學生會由于一些思維習慣或不精確的繪圖導致錯誤的結果,而GeoGebra在動態顯示、直觀性、精確性上表現得非常優秀,將其與日常物理教學相結合,可收到事半功倍的效果。
參考文獻
[1]殷正徐,吳偉.GeoGebra軟件在高中物理課堂教學中的案例應用分析:以簡諧振動和機械波為例[J].物理教師,
2017(10):70-73.
[2]呂艷坤,吳瀟.基于科學思維進階的力學動態平衡變式分析[J].物理教學,2019(5):49-51.

