小樣本數據條件下進行精確等級賦分的探究
丘清文
摘要:新高考以等級分呈現,等級賦分是以一個省的數據為基礎,而學校組織的各類考試屬于小樣本數據,不能簡單套用高考賦分模式,如何給校內考試進行合理、精確的等級賦分?本文從分析等級賦分的計算方法開始,運用圖形對比法,大膽進行假設,建立數學模型,形成計算模板,在實際應用中進行驗證,取得了理想的效果。
關鍵詞:新高考;等級賦分;計算方法
新高考改革之后,學生選考有多種組合,因試卷難度不同,考試內容不同,原始分不能直接相加。進行等級賦分就是對選考科目進行加權處理,以保證不同選考組合的學生能在一起排序。對于高中學校,更多的是學校自行組織的校內考試,等級賦分的準確性對教學評價的指導意義是十分重要的。
一、高考等級賦分的計算
根據廣東省教育廳關于等級賦分相關文件的描述,等級賦分分三個步驟:排序、劃等級、賦分,即把對應考試科目的所有考生群體依據卷面分從高到低進行排序;按一定的人數比例將該選考科目考生群體劃分為若干個等級,每個考生按照其卷面分在該選考科目考生中的排位,對應到某個等級;根據考生的卷面分、所在等級的賦分區間,運用等比例轉換法則將其卷面分換算成等級分。
二、小樣本數據條件下精確等級賦分的可行性分析
1、計算公式中不確定項的分析
在等級賦分計算公式s2-s0s0-s1 =t2-t0t0-t1 中,s0(考生原始得分)是已知的,考生對應等級的t1和t2(相應等級的賦分下限和上限)是確定的,t0是需要的計算結果(學生等級分),在小樣數據下不能確定的變量只有s1和s2(等級所對應卷面分區間的下限和上限)了。只要正確找到s1和s2值,就能精確計算出該考生的等級分。
2、推導s1和s2值的過程
在高考等級賦分的計算中s1和s2值是確定的,而作為小樣本數據的學校考試的等級賦分計算中s1和s2值之所以不能確定,根本原因是沒有全省全樣本數據的支持從而不能準確確定學校考試成績的相對位置。但當滿足以下兩個條件:學校每屆高考均分成績相對穩定、全省成績分布符合正態分布,通過圖形化,s1和s2值是可以計算出來的:
1.全省成績分布符合正態分布:鑒于高考試卷的高質量和全省考生數量,這個假設條件成立的可信度會很高;
2.學校每屆高考均分成績相對穩定:對于一個班級較多,教學質量穩定的學校,這個假設條件也是成立的。
三、具體實施
運用EXCEL的計算和圖表功能做出一個EXCEL模板,模板有三個工作表:“數據處理”、“數據監測與調整”和“數據輸出”。粘貼卷面成績到“數據處理”表中,人工設置學校均分與省均分的偏移值、預測省最高分和最低分這三個參數,通過監測指標和圖形再進行微調,便可自動完成等級賦分。
“數據處理”表主要功能:
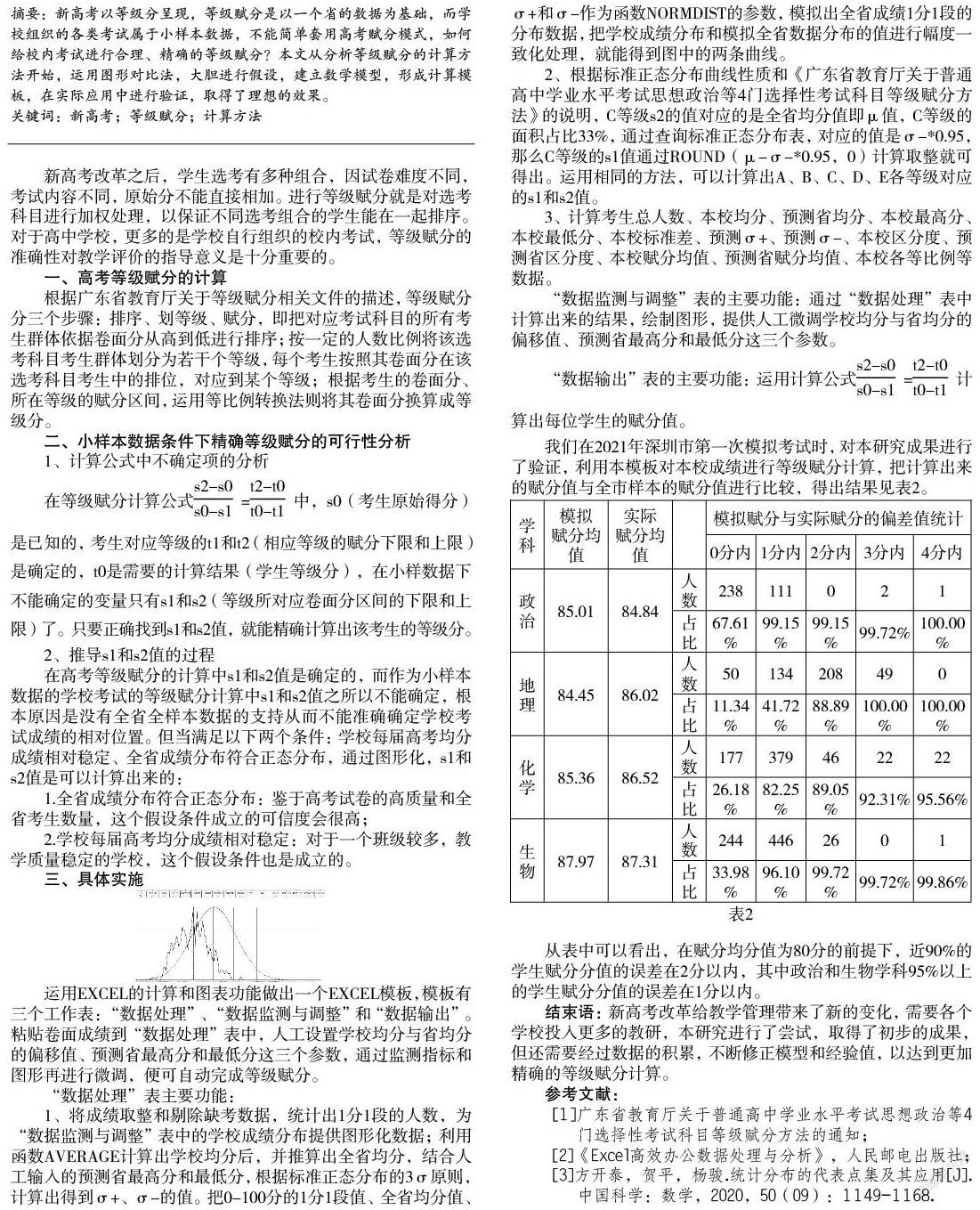
1、將成績取整和剔除缺考數據,統計出1分1段的人數,為“數據監測與調整”表中的學校成績分布提供圖形化數據;利用函數AVERAGE計算出學校均分后,并推算出全省均分,結合人工輸入的預測省最高分和最低分,根據標準正態分布的3σ原則,計算出得到σ+、σ-的值。把0-100分的1分1段值、全省均分值、σ+和σ-作為函數NORMDIST的參數,模擬出全省成績1分1段的分布數據,把學校成績分布和模擬全省數據分布的值進行幅度一致化處理,就能得到圖中的兩條曲線。
2、根據標準正態分布曲線性質和《廣東省教育廳關于普通高中學業水平考試思想政治等4門選擇性考試科目等級賦分方法》的說明,C等級s2的值對應的是全省均分值即μ值,C等級的面積占比33%,通過查詢標準正態分布表,對應的值是σ-*0.95,那么C等級的s1值通過ROUND(μ-σ-*0.95,0)計算取整就可得出。運用相同的方法,可以計算出A、B、C、D、E各等級對應的s1和s2值。
3、計算考生總人數、本校均分、預測省均分、本校最高分、本校最低分、本校標準差、預測σ+、預測σ-、本校區分度、預測省區分度、本校賦分均值、預測省賦分均值、本校各等比例等數據。
“數據監測與調整”表的主要功能:通過“數據處理”表中計算出來的結果,繪制圖形,提供人工微調學校均分與省均分的偏移值、預測省最高分和最低分這三個參數。
“數據輸出”表的主要功能:運用計算公式s2-s0s0-s1 =t2-t0t0-t1 計算出每位學生的賦分值。
我們在2021年深圳市第一次模擬考試時,對本研究成果進行了驗證,利用本模板對本校成績進行等級賦分計算,把計算出來的賦分值與全市樣本的賦分值進行比較,得出結果見表2。
從表中可以看出,在賦分均分值為80分的前提下,近90%的學生賦分分值的誤差在2分以內,其中政治和生物學科95%以上的學生賦分分值的誤差在1分以內。
結束語:新高考改革給教學管理帶來了新的變化,需要各個學校投入更多的教研,本研究進行了嘗試,取得了初步的成果,但還需要經過數據的積累,不斷修正模型和經驗值,以達到更加精確的等級賦分計算。
參考文獻:
[1]廣東省教育廳關于普通高中學業水平考試思想政治等4門選擇性考試科目等級賦分方法的通知;
[2]《Excel高效辦公數據處理與分析》,人民郵電出版社;
[3]方開泰,賀平,楊駿.統計分布的代表點集及其應用[J].中國科學:數學,2020,50(09):1149-1168.

