指向“數學眼光”發展的綜合與實踐

周靜珠

【摘? ?要】小學數學教材中的綜合與實踐內容以學生感興趣的實際問題為素材，引導學生通過數學思考，或建構模型或給出方案或解決問題，是發展學生數學眼光的好素材。以綜合實踐內容“自行車速度里的奧秘”為例，教師可采用以下教學策略，培養學生的數學眼光：用數學眼光洞察，變“現象”為“問題”，促進數學意識的生長;用數學眼光論證，從“猜想”到“實踐”，促進數學思想的形成;用數學眼光創見，能“質疑”會“創造”，促進綜合能力的提升。

【關鍵詞】自行車速度里的奧秘;綜合實踐;數學眼光

學生往往在應用數學的思想和方法解決問題的過程中，尋求對現實世界現象的認識和理解。數學的眼光由此得以發展。數學眼光是一種意識，一種能敏銳地把實際問題抽象成數學問題的意識;數學眼光是一種思想方法，一種能借助分析、推理，探求事物中隱含著的數學結構的方法;數學眼光是一種綜合能力，一種能綜合運用所學知識，活學活用的能力。小學數學教材中的綜合與實踐內容以學生感興趣的實際問題為素材，引導學生通過數學思考，或構建模型，或給出方案或解決問題，是發展學生數學眼光的好素材。下面以人教版六年級下冊“自行車里的數學”為例，談談如何基于“綜合與實踐”活動發展學生的數學眼光。

【案例背景】

“自行車里的數學”是在學生學習了“比例”單元后編排的綜合與實踐活動，活動以自行車“蹬一圈能跑多遠”為研究問題，主要探索“前后齒輪比與自行車蹬一圈行進路程”之間的關系。教學時如果按照教材直接呈現研究問題，引導學生進行探索，會缺少讓學生自主發現問題、提出問題的過程。直接呈現問題還會讓研究的內容僅限于前、后齒數的比值上，缺少對所涉及知識的綜合應用的探究。為此，教師對該活動進行了改造，把“自行車里的數學”改為“自行車的哪些設計與速度有關”，將研究兩個問題改成了研究四個子問題（如表1），使研究更有現實價值。

這樣的改造使得探究活動更為綜合，研究的問題不僅指向比例的知識，更鏈接了圖形的知識，應用圖形的特征解釋生活現象的原理，應用圓的周長公式解決自行車輪胎大小的問題等等。生活中的實際問題具有復雜性和多樣性，改造后的學習設計更貼近真實世界，便于教師引領學生從數學的視角進行觀察、分析、建模、解答、反思，發展學生的模型思想、運算能力、應用意識和創新意識。

【案例再現】

（一）數學眼光洞察：經歷“現象—問題”的過程

1.情境驅動

播放變速自行車與普通自行車進行競速比賽的視頻。請學生思考：看了這段視頻，你能提出什么問題？

2.形成驅動問題

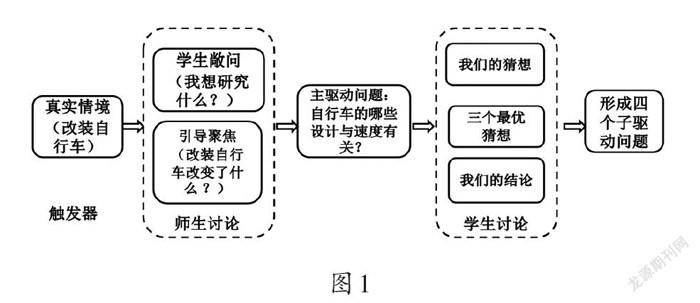
驅動問題：自行車的哪些設計與速度有關？

3.構建研究方案

（1）學生自主提出初步猜想。

影響自行車速度的因素可能有：輪胎大小、腳踏板蹬的速度、自行車的齒輪數、車輪的形狀、人騎車的姿勢、車輪一周的長度、車把手的形狀……

（2）小組討論篩選最優猜想。

四人小組討論，針對“自行車的哪些設計與速度有關”這個問題選出最優猜想，形成小組意見（如腳踏板蹬的速度確實能夠影響自行車的速度，但是這個因素不屬于自行車的設計，因此不納入最優猜想之中），并全班交流。

（3）學生匯報形成子問題。

通過小組匯報，討論下階段研究的方向，形成子問題。

（二）數學眼光論證：經歷“猜想—實踐”的過程

學生對四個子問題的研究，都經歷了“小組共識，聚焦猜想→小組討論，形成方案→合作探索，驗證猜想→構建模型，得出結論”的過程。下面以子問題4“齒輪的設計與速度有什么關系”為例具體展開。

1.小組共識，聚焦猜想

思考：研究“齒輪的設計與速度有什么關系”，可以從哪些方面入手？

想法一：研究前齒輪數、后齒輪數的比值。

學生理由：因為知道齒數和轉的圈數成反比例，前齒輪數×轉的圈數=后齒輪數×轉的圈數=總齒數（不變），所以前齒輪數與后齒輪數的比值就是蹬一圈后齒輪轉幾圈，后齒輪轉幾圈，就是后輪轉幾圈。

想法二：研究車輪的周長。

學生理由：通過觀察，自行車是通過腳蹬踏板，帶動前齒輪、鏈條、后齒輪，最后帶動后輪轉動才往前走的。所以只知道后輪轉了幾圈還不夠，還需要知道車輪周長。

想法三：研究自行車蹬一圈能走多遠。

學生理由：要研究齒輪與速度之間的關系，可以先研究蹬一圈，然后通過蹬一圈走多遠來推測自行車的速度。

教師建議：研究了前面兩個想法就可以研究第三個想法了。

2.小組討論，形成方案

師：剛才已經討論出了需要研究的要素，現在要知道它們的具體數據，有什么好方法？

生：可以數一數齒輪數，可以量一量車輪的周長，還可以先測量再計算。（板書：數、量、算）

3.合作探索，驗證猜想

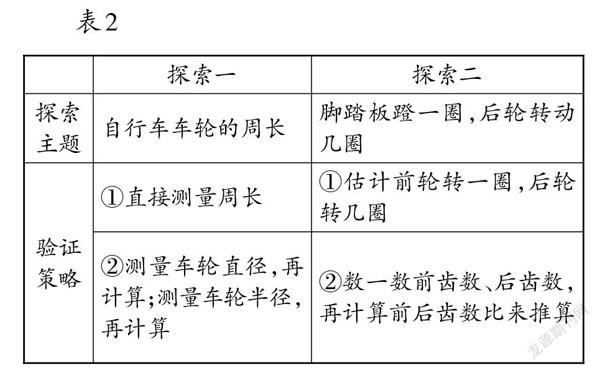
教師出示表2，請學生驗證猜想。

師：車輪的周長是怎么得到的？

生：通過直接測量車輪的周長;先測量車輪半徑，再通過計算得出車輪周長。我們是先測量了車輪的直徑，再計算車輪的周長。

師：比值怎樣得到？表示什么？

生：這個比值是用前齒輪數除以后齒輪數得到的，是前后齒輪數的比值。

師：周長為什么要去乘前齒輪數與后齒輪數的比值？

生：因為齒輪數與轉的圈數成反比例關系，所以前齒輪數與后齒輪數的比值就是前齒輪轉1圈，后齒輪轉幾圈，也就是后輪轉幾圈。

4.構建模型，得出結論

模型一：前齒輪數÷后齒輪數×車輪周長=蹬一圈的路程

模型二：蹬一圈的路程×單位時間蹬的圈數=單位時間行駛的路程（速度）

（三）數學眼光創見：經歷“質疑—創造”的過程

師：如果運用今天所學的知識來設計一輛自行車，你們準備怎么設計？

生：可以把自行車的車輪設計得大一點。

生：那車輪也不能無限大吧！如果車輪很大很大，根本就不能騎了。

生：前后齒輪比大，也就意味著蹬一圈，后輪轉動的圈數多。那是否可以讓前后齒輪比隨意增大？

生：如果前后齒輪比大，確實蹬一圈能夠使后輪多轉幾圈。可是太大了，我們會不會騎不動？

生：變速自行車就是改變了前后齒輪比，每一種行駛的速度都有所不同。

……

【教后反思】

“綜合與實踐”板塊以與學生生活密切相關的各類具有現實性、綜合性、實踐性特征的問題為抓手，以自主探究為主要學習方式，其教學內容是發展學生數學眼光的重要載體。以“數學眼光”的培育為目標進行教學時，教師要關注以下幾點。

（一）驅動問題變“給予”為“內生”，促進數學意識的生長

綜合與實踐活動以問題為抓手，因而驅動性問題的設計至關重要，一個好的驅動問題能夠為學習者提供一個廣闊的、多向度的探索空間。它既能激發學生學習的內在動力，也能提綱挈領地為學生指出持續思考、自我探究的方向。

教學實踐中，教師容易從知識本位出發，直接把經過加工、改造的問題拋給學生，而忽視了學生自發地從現象中發現并提出自己想要研究的問題的過程。而單純地讓學生漫無邊際地提問，也會使研究的方向不清晰。因此，驅動問題的產生，應該是師生共同交流并達成共識的過程，也是學生問題“內生”的過程。

要讓驅動問題真正“內生”，首先就要創設一個真實情境，這個情境好比是一個觸發器，能夠引導學生產生問題，然后在師生的交流中不斷讓問題聚焦，逐步形成驅動問題。接下來，需要學生根據產生問題的情況提出自己的猜想，并在小組中分析、對比、交流，集中大家的意見，形成研究的主要方向。圖1反映了驅動問題“自行車的哪些設計與速度有關”的“內生”過程。學生只有不斷經歷這樣的“內生”過程，才會擁有敏銳的數學眼光，并自覺地去洞察大千世界，從紛繁的表面現象中抽離出數學問題。

（二）探究過程變“形式”為“實質”，促進數學方法的發展

綜合與實踐以自主探究為主要學習方式。在探究活動中，如果學生按照教師設計的探究路徑一步一步走，那么學生僅僅是一個簡單的操作工，而不是獨立思考、研究的個體，無法很好地達成對研究過程的感悟，對數學思想方法的體會。同時，如果缺少指導的探究，學生就會無所適從，找不到研究的方向。因此，教師可以從數學問題探究的一般方法入手，找到普適的方法，給予學生指導。

“猜想—研究—結論”是學生解決數學問題的基本步驟。因此，教學中，教師要引導學生先各自進行猜想，然后討論各自的猜想是否合理，是否指向需要解決的問題，接著根據猜想，開展計數、測量、計算、推理等一系列數學活動，從中感悟方法、提升能力，最后通過探究得到相關的數據，并進一步對這些數據進行分析、綜合，逐步形成學習成果——數學結論或數學模型。

探究活動以學生為主體，學生在教師的引導和點撥下，經歷科學檢驗的歷程，在全方位的思維活動中達成對數學思想方法的認知，發展數學眼光。

（三）學習評價變“單一”為“豐富”，促進綜合能力的提升

教師要引導學生用數學的眼光審視本人和他人在學習過程中的表現，從提出問題、敢于猜想、探索研究、合作交流、達成目標等維度展開自我評價和相互評價。在自評和互評中，學生總結、梳理學習的全過程，推動綜合能力的提升。

總之，綜合與實踐的教學，是引導學生用數學的眼光觀察現實世界，從表面現象中抽象出數學問題并進行數學探究的重要渠道。讓學生在實踐中，養成從數學角度觀察現實世界的意識與習慣，提升洞察力、論證力、創造力，就是在培育學生的核心素養，發展學生的數學眼光。

參考文獻：

[1]孫曉天，邢佳立.中國義務教育：基于核心素養的數學課程目標體系：孫曉天教授訪談錄[J].教學月刊·小學版（數學），2021（11）.

[2]胡晉賓，劉洪璐.數學眼光的內涵及培養[J].中學數學月刊，2021（2）.

[3]夏雪梅.項目化學習設計：學習素養視角下的國際與本土實踐[M].北京：教育科學出版社，2018.

[4] 劉月霞，郭華.深度學習：走向核心素養[M].北京：教育科學出版社，2018.

（浙江省寧波市海曙區海曙中心小學? ?315000）