第一學段數學教學中孕伏早期代數思維的實踐探索

王孫君

摘 要：結合第一學段數學教材中數與運算教學，讓學生感知符號意識和量與量之間的結構關系思維，理解簡單的代數方式和代數關系，能促進學生早期代數思維的萌發。

關鍵詞：第一學段;數學教學;早期代數思維

數學教育中，代數思維被認為是數學的“核心思想”。從20世紀開始，數學教育家們就非常注重代數思維的早期培養。根據2018年修訂的《義務教育數學課程標準》有關“數與代數”領域的目標要求，現行教材采取了分散滲透與集中安排相結合的方式編排代數課程內容，從低年級適度地早期孕伏，逐步過渡到高年級初步集中學習。如何在第一學段教學中融入早期代數思維，幫助學生理解簡單的代數方式和代數關系？ 現把我們的實踐與同行分享。

一、研析教材中早期代數課程資源

我們課題組潛心研讀、梳理了人教社第一學段教材能融入早期代數思維教學的有關典型習題，整理成下表。

上述典型習題均融合在專項練習中，其宗旨為：

1.初步了解符號意識和等號的相等關系性質

教材結合數與運算內容，有機安排了“在符號中填上合適的數”，如□-10=4、3×（）=（）×（）、12=〇+〇+〇等。其目的為：一是讓學生知道口與（ ）、〇等既可以表示填寫數的空位，也可以用來表示數;二是幫助學生理解等號內含的關系性質：等號也表示相等且左右相等的符號，從而突破“等號左邊是運算、右邊是結果，等號是用來連接算式和得數的”這一程序性質的局限。

2.初步感知量與量之間的結構關系思維

結合問題解決，分析概括出量與量之間關系性元素，把其潛在的結構表達出來。如二上：1只青蛙1張嘴，2只眼睛4條腿;2只青蛙（ ）張嘴，（ ）只眼睛（ ）條腿;照這樣說，一直說到6只青蛙。這一過程所內涵的規律、相等關系把數量提高到一般化、概括化的高度，其實質就是學生代數思維外顯的結果。

二、探尋代數思維萌發的方法路徑

（一）激活已有經驗，感知符號意識

1.在多元接觸中感知符號的數學價值

一上比較兩個數的大小時，學生就開始接觸=、〉、〈，初步感知這些符號是用來比較兩個數的大小關系，等號是用來連接式和得數。學習10以內的加減法時安排了如：7+□=8、4+？=6，讓學生知道□、？ 等可以表示一個數。這是最早的符號意識的感知。

2.在多維感悟中理解等號的關系性質

（1）在認數操作時感知 “認識6”時，先引導學生從學具袋中挑出自己喜歡的6個學具，把它們分成兩堆并說一說。后設問：有的小朋友擺了一種，有的擺了兩種，還有的更多，怎樣才能把五種情況一種不漏地擺出來呢？有沒有更好的辦法？討論反饋后，追問：6可以分成幾和幾，你能用算式表示嗎？師板書：6=1+5，6=5+1，6=2+4，6=4+2，6=3+3。接著讓學生觀察思考：這些算式和以前學習的有什么不同？學生發現以前的算式加號在等號的左邊，這些算式加號在等號的右邊。使學生認識到等號不只是從左到右的運算符號，還可以表示左右兩邊是一種相等關系。

（2）在計算推理時理解 20以內加減法中，安排了很多用□表示未知數，如□-10=4，讓學生再次理解□可以表示數，等號表示左右兩邊相等關系。100以內加減法中，安排了其他符號表示未知數，進行推理，如口一（ ）=△ 等等。有余數除法中還安排了“□÷□=6……1，被除數最小是（）”。學生解答在這些算題的過程中，促進了對等號表示左右兩邊相等關系的理解。這是方程核心思想的孕伏。

3.在比較發現時理解等式的關系結構

教學“9 加幾”時，讓學生擺一擺小棒來發現“湊十法”：9+3，把3分成 1 和2，9 和 1 湊成 10，所以 9+3=12。例題教學和鞏固練習后，引導學生比較發現：我們是怎么計算9加幾的？都是先加上1和9湊成10，然后后面加數減去1，加上的1減去的1剛好抵消，結果不變。即（9+1）+（3-1）=9+3，（9+1）+（5-1）=9+5，在比較發現的基礎上讓學生用語言表達出來。這一隱含的等式關系結構a+b=（a+1）+（b-1）的感知和理解，在學習“湊整”法時進行了巧妙運用。

（二）遵循認知規律，感知數量間的結構關系

1.多元化思考表述，發展結構意識

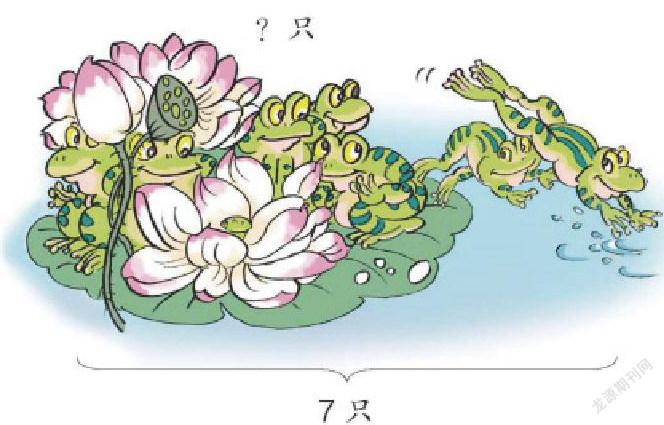
教材中安排了很多圖文信息題，讓學生解決。如一年級上冊下圖：

題目要求“荷葉上還剩幾只青蛙”。有的同學根據部分與總體的關系，用減法來解決：一共有7只青蛙，減去跳走的 2只，等于荷葉上還剩的青蛙，7-2=5;有的用加法來解決：荷葉上還剩的青蛙加上跳走的2只，一共是7只，（5）+2=7。這兩種表述都正確，第二種雖然比第一種思路稍煩些，但卻是方程思維方式的顯現。它不僅有助于學生對“一共、跳走、還剩”三者之間數量關系的整體把握，加深學生對數量關系的理解，還滲透了用（）表示未知數參與運算。教師要有意識地引導學生由程序性的算法7-2=5，逐漸向關系性算法（）+2=7轉變，這正是算術思維向代數思維的轉變。

低年級問題教學中，借助直觀的圖文信息，引導學生用多種方法進行解決，并用語言把思路表述出來，這樣將算術與代數方法并舉，讓學生在過程中經歷思維結構的轉化，感知兩種思維方式之間的差異，逐步發展學生的代數結構意識。

2.規律性推理識別，孕伏函數關系

二上62頁數青蛙的數學游戲：1只青蛙1張嘴，2只眼睛4條腿;學生馬上回答：2只青蛙2張嘴，4只眼睛8條腿。這么快就說出來了，你們是怎么想的？生馬上回答：1只青蛙1張嘴，2只眼睛4條腿;2只青蛙2張嘴，2×2=4只眼睛2×4=8條腿。那3只青蛙呢？3只青蛙3張嘴，3×2=6只眼睛，3×4=12條腿。那4只青蛙？4只青蛙4張嘴，4×2=8只眼睛，4×4=16條腿。你們發現了什么？我們發現了幾只青蛙，就是幾×2只眼睛，幾×4條腿。你們是怎么發現這個規律的？因為每只青蛙都有2只眼睛，所以幾只青蛙就是幾×2只眼睛，每只青蛙都有4條腿，所以幾只青蛙就是幾×4條腿。在老師不斷追問下，學生探尋推理出了規律并加以運用，有機孕伏了函數關系。

3.操作性等量傳遞，培育方程意識

二下圖示天平教學，以天平為支撐，讓學生經歷動手增減變換、讓天平平衡的過程中初步滲透方程的性質，感悟多種等式的結構。又如“克和千克”單元思考題的學習：從圖中你發現了什么？生回答：1只鵝=2只鴨，3只雞=2只鴨。你是怎么知道1只鵝=2只鴨？天平的左邊放著1只鵝，右邊放著2只鴨，我們發現天平的兩邊剛好平衡，所以1只鵝=2只鴨。右邊天平也是平衡的，左邊3只雞，右邊2只鴨，所以3只雞=2只鴨。那一只鴨和一只雞的重量是多少呢？因為1只鵝=2只鴨，1只鵝=6千克，所以2只鴨=6千克，1只鴨=6÷2=3千克。那1只雞有幾千克呢？1只鵝=2只鴨，3只雞=2只鴨，所以1只鵝=3只雞，也就是3只雞=6千克。1只雞=6÷3=2千克。這一歷程讓學生認識到了相等關系的傳遞性，浸潤了方程思想。

我們堅信：教師們在提升第一學段學生數學能力的同時，注重知識的“生長點”與“延伸點”，對運算問題進行“代數地思考”，一定能發展學生的早期代數思維。

參考文獻：

[1] 王薇.基于算術教學，滲透代數思維[J].數學教學通訊，2018（04）.

（此論文為G2019179浙江省教研室規劃課題《小學階段代數思維培養的實踐研究》研究成果）

3909501908297