基于教學實踐的高中數學創新學習再思考

摘 要：教學實踐是指教師將自己所掌握的教育理念、教學方法運用在具體的學科課堂教學行為之中，是踐行教育思想觀念的體現.當教師掌握了創新學習模式，并將其運用于高中數學教學之中后，又從教學實踐中總結出了新的教學經驗與感悟，這就是教師基于教學實踐后對創新學習的再思考，是教師優化教學手段，更加科學合理地運用創新學習模式開展高中數學教學活動的主要途徑.基于此，本文立足于教學實踐的視角，對高中數學創新學習的有效實施提出了以下幾點建議，以供參考.

關鍵詞：教學實踐;高中數學;創新學習;再思考

中圖分類號：G632????? 文獻標識碼：A????? 文章編號：1008-0333（2021）36-0030-02

在教育改革不斷深化的背景下，如何突出學生的學習主體性，指導學生掌握創新學習的方法，轉變傳統的固有學習模式，成為了眾多教師關注的問題.在創新學習模式的實施過程中，對教師提出了更高的要求，因此創新學習是一種新型教學模式，雖然在大量的教學嘗試中收獲到了一定的成效，但是其在課堂教學中的運用并不成熟，需要教師在將其運用在高中數學教學實踐的過程中，不斷地吸取經驗，能夠結合具體的教學情況，逐漸地優化創新學習模式的實施策略，以促進高中生的數學學習質量提升，推進高中生在數學創新學習中的全面發展.

一、創新學習在課前預習教學中應用的再思考

通過在教學實踐的分析中，發現創新學習模式與傳統的教學模式最本質的區別在于更加重視學生學習的自主性，這種自主性體現在學生學習的全過程，要求學生在創新學習中通過自主學習鍛煉獨立思考能力與問題解決能力，能夠在快樂的學習中獲得成長與進步.課前預習為學生的數學獨立學習提供了一個最佳的平臺，可以讓學生在數學預習中主動地搜集學習資料，在預習中勤于挖掘課程問題，勇于探索數學問題，以創新學生的預習學習方式，為課堂學習做好準備.

以《空間點、直線、平面之間的位置關系》為例，這節課的內容雖然難度不高，但是需要學生記憶的知識點卻比較多，為了避免高中生在數學學習中對數學概念與定理采取死記硬背的學習方式，教師應運用創新學習模式對學生的課前預習給予指導.如在“平面”的這一概念知識點預習中，要讓學生認識到數學“平面”概念理解的預習學習并不是直接地翻閱課本，閱讀“平面”的概念后進行總結，之后強行地記憶數學概念，而是要在預習學習中自行地開展有趣的、新穎的數學探究實驗，學會在數學概念的預習學習中借助身邊的實物去理解“平面”的概念與基本屬性、特質，并將探究實驗中發現的“平面”知識點記錄下來，為接下來的課堂學習做好準備.這樣的創新預習學習方式，可以培養學生的獨立思考能力，在預習環節中通過探究實踐理解數學概念，帶著預習中沒有解決的問題進入到課堂學習中，可以提升學生的學習專注力.

二、創新學習在數學情境創設中應用的再思考

在過去的創新學習模式過程中，教師雖然結合教學內容創設了數學情境，但是這些數學情境的創設存在兩個問題：第一，無法由情境的創設激起學生的學習興趣;第二，情境創設缺乏創新探索的環節，只能起到一些調節課堂氛圍的作用，這種過于形式化的數學情境創設不利于創新學習模式的有效實施，對此，需要教師優化創新學習模式實施中的情境創設方式，能夠在情境創設中提出具體化的探究問題，吸引學生參與到課程問題的深度思考中，并能夠對問題展開創新性的探索.

以《橢圓的定義與標準方程》的知識點教學為例，教師首先可以創設生活化教學情境，如情境1：“在圓柱狀的水杯中裝半杯水，先將水杯放在水平的桌面上，觀察水面呈現的是圓形，當人們想要喝水的時候，水杯傾斜，在觀察水平面會發現其截面變成了什么形狀？”由此引出《橢圓》的定義，并由此提出問題：“生活中有許多橢圓的圖形，你還知道哪些呢？”，為了引領學生從已知經驗過渡到新知識的探索，培養學生的知識遷移能力，教師可以創設這樣的情境;情境2：“請學生們回憶一下圓的畫法、定義以及標準方程的形式，猜想橢圓的畫法、定義與標準方程式有是什么樣子的呢？”以情境的創設引領學生學會類比推理，引發學生對問題思考的積極性，能夠在創新的數學情境帶領下主動地加入到創新學習活動中.

三、創新學習在數學合作教學中應用的再思考

任何的科學知識總結都需要經歷長期的觀察與探索，高中數學課程知識的學習同樣如此.但是，在過去的課堂教學中教師忽視了學生知識學習的過程性，一味地將書本中數學家們已經總結出的數學經驗直接傳達給學生，這種情況下學生的數學學習失去了探究的意義，只知道數學知識與數學規律的結果，而沒有掌握知識學習與規律總結的方法，不利于高中生的數學學習能力提升.而基于教學實踐視角下的創新學習主張學生在學習全過程中的參與，在對創新學習模式實施的再思考后，發現小組合作方式對學生的創新學習具有促進作用，那么教師就可以開展小組合作學習活動，助力學生的創新學習.

如在函數的教學之后，教師給學生出示了這樣一道題的解題過程：

已知（x+2）2+y2/4=1，求x2+y2的取值范圍.一名學生的解題過程如下：

解 ∵（x+2）2+y2/4=1

∴y2=-4x2-16x-12

∴x2+y2=-3x2-16x-12=-3（x+8/3）2+28/3

因此，當x=-8/3時，x2+y2有最大值為28/3，

又∵x2+y2≥0，

∴x2+y2的取值范圍是[0，28/3]

請學生們以小組為單位，分析這個問題的解答過程與結果是否正確，如果不正確，是哪里出錯了呢？并要求學生們運用還原法、代值法進行這道題的推演驗證.在此過程中，教師通過錯題展示的方式，引發了學習小組對數學習題解答與計算的熱情，接下來學生們會嘗試通過不同的途徑來驗證答案的正確性，試圖找到此題的不同解法，以實現高中生的數學學習方法創新，助力學生在創新學習中的推理能力以及多樣化解題能力提升.

四、創新學習在課后復習指導中應用的再思考

課后復習不僅僅是學生對已經學習過的數學知識回顧，同時更是學生對問題反思以及自我學科素養發展的一個重要過程，因此在高中數學教學中教師應善于優化課后復習指導工作，將創新學習模式融入到課后復習的指導中，讓學生在自我的反思與修正中正視自我，進而形成學科核心素養.在過去的高中數學創新學習中，部分教師對學生的課后復習指導過于形式化，學生的復習學習缺乏針對性，從而影響了創新學習實施的教學效果，這些問題迫切地需要解決，才能保障課后復習創新學習模式的有效性得以提升.

以《指數函數的課后復習》為例，為了提升課后復習指導的針對性，教師可以設計分層復習作業，為不同層次的學生布置不同難度的課后復習作業內容，如：

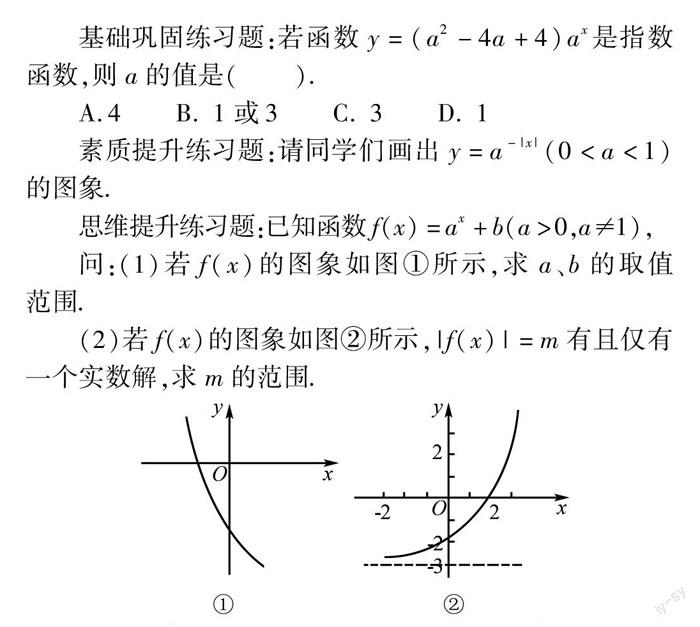
基礎鞏固練習題：若函數y=（a2-4a+4）ax是指數函數，則a的值是（? ）.

A.4? B. 1或3? C. 3? D. 1

素質提升練習題：請同學們畫出y=a-|x|（0思維提升練習題：已知函數f（x）=ax+b（a>0，a≠1），

問：（1）若f（x）的圖象如圖①所示，求a、b的取值范圍.

（2）若f（x）的圖象如圖②所示，|f（x）|=m有且僅有一個實數解，求m的范圍.

以上三個問題的提出主要是泛指此三類難度的類型題設計，通過分層的課后習題練習布置與針對性的指導，為高中生的課后創新學習提供了助力.分層習題布置的方式，符合因材施教的教育理念，可以滿足不同層次學生的數學學習需求，讓優秀生可以在難度較高的習題解答中產生挑戰欲，對課后習題的完成保持足夠的熱情，而難度相對較低的問題設計，可以讓中低層次的學生從習題解答中獲得成就感，樹立學習數學的自信，同時可以從習題解答中查缺補漏知識點，發揮課后練習的作用，讓全體學生都可以在創新的課后學習過程中獲得進步.

總之，創新學習是課程改革以及學生全面發展的需求，也是促進學生數學核心素養生成的需求，高中數學教師應積極地引導學生創新學習，將創新學習理念有效地實踐于數學課堂教學中，帶領學生在課前預習、情境學習、合作探索以及課后訓練等環節中落實創新學習，轉變高中生的數學學習方式，讓高中生掌握更加有效的數學學習方法，以提升教師的數學教學質量與效率，達到授之以漁的目的.

參考文獻：

[1]湯瑋.淺談高中數學創新學習的教學策略[J].課程教育研究，2017（08）：133.

[2]金伶俐.新媒體背景下高中數學教學實踐與思考[J].中學生數理化（教與學），2017（12）：33.

[3]馬學堅.高中數學課堂教學中創新學習模式的應用[J].科學咨詢（教育科研），2021（05）：164-165.

[4]郎志媛.創新學習模式在高中數學課堂教學中的應用分析[J].數學學習與研究，2013（13）：138.

[5]趙曉娥.高中數學研究性學習教學及其創新設計分析[J].考試周刊，2020（A0）：71-72.

[責任編輯：李 璟]

收稿日期：2021-09-25

作者簡介：張必榮（1983.4-），男，江蘇省如東人，本科，中學一級教師，從事高中數學教學研究.