運用適時點撥，提升思維品質

趙碧泉

[摘? 要] 在小學數學課堂教學中，提升學生的數學思維品質是重要的教學目標，教師是學生數學學習的引導者，運用適時點撥能夠有效地提升學生的思維品質。基于此背景，文章對在“重復時”點撥，突破思維僵局;在“困惑時”點撥，引發思維頓悟;在“生長處”點撥，引導思維概括;在“錯誤處”點撥，深化數學理解的策略進行了探究。

[關鍵詞] 小學數學;教學;適時點撥;思維品質

在小學數學教學實踐中引入“慢藝術”，可以聚焦學生的情感體驗，特別是針對新知的教學過程或者是具有創造性的教學環節中，逐漸放緩的教學節奏，能夠使學生全身心地投入其中，并且展開主動思考，順利突破教學重點和難點。教師在學生學習數學的過程中，進行適時點撥，能夠有效地提升學生的思維品質。

一、在“重復時”點撥，突破思維僵局

教師在課堂教學過程中要拋出具有開放性的問題，要讓學生立足于不同的方法展開解答，目的是為了更好地培養學生的發散性思維，但是很多學生卻在一條道上走到黑。此時就需要教師把握恰當的時間，對學生進行點撥和啟發，確保課堂資源的正向生成。

例如，在教學“兩步計算應用題”時，我首先為學生創設了真實的情境：為了表揚班級內學生的積極表現，老師購買了40支筆，并打算分給8個不同的小組，每個小組能夠分到幾支？在這一問題情境創設之后，我要求學生對其中的條件進行改變，將其轉化成為一個需要經過兩步計算的應用題。

師：如果我們所購買的筆的支數是不知道的，可以如何設計問題？

生1：可以說買了5盒筆，每盒筆有8支。

師：回答得非常好！大家還有不同的提問方法嗎？

生2：老師購買了4盒筆，每盒有10支。

師：還有嗎？

接下來學生所提出的是每盒20支、一共購買2盒的方法，很顯然這樣下去，不管是思考還是回答都毫無意義，于是我及時對學生進行點撥：剛才大家使用了怎樣的方法將40支筆進行了轉換？

學生回答是根據乘法。于是我繼續追問：是否還可以選擇其他的計算方法呢？

經過我的進一步引導和啟發，學生展開了新的思考，實現了新的生成。

上述教學案例中，學生飽含熱情地探討，但是卻因為生1的思維受到了強烈的暗示，產生了定式，所以具體的回答仍停留在原地，難以取得突破，此時便是教師給予點撥和啟發的最佳契機，帶領學生突破思維的禁錮，為學生提供更廣闊的思考空間，使其思維往縱深拓展。

二、在“困惑時”點撥，引發思維頓悟

數學學習過程中不可缺少教師的有效介入，如果僅依靠學生自主展開單純的研習，很有可能偏離原有的方向，也容易被其他因素所干擾，因此教師需要在具體的學習過程中及時審視學生的學習狀態，準確把握學生的困惑處、混沌處以及存在爭議之處，并及時給予援助和啟發，這樣學生的思考及學習才能具備正確的方向。

例如，一位教師在教學“最簡分數”一課時，有這樣一個教學片段。

生1：我認為最簡分數就是分子和分母都有公因數1。

師：大家認為他的回答對嗎？是否可以舉例說明？

生2：在 和 中，分子和分母都含有公因數1，但是它們卻都不是最簡分數。

生3：所以我們應當強調的是“只有”，公因數只有1的情況才是最簡分數。

師：大家再次反復品味這句話，是否有其他不同的感受？

生4：我認為他表達得不夠完整，漏掉了“分數”二字。……

……

上述教學片段中，教師的點撥十分簡單，但是卻能夠對學生形成積極有效的引導，使學生聚焦同伴的發言，真正體會最簡分數的真義。這樣的引領能夠明確學習的方向性，利于就此生發辨析以及思考等一系列思維活動，同時也能夠聚焦學生的數學表達，提升表達的規范性。在這一教學過程中，學生有了對概念的個性化理解，建立了嚴謹的數學思維。

三、在“生長處”點撥，引導思維概括

實際教學過程中，教師應準確把握知識的生長點，引導學生借助數學語言進行表達，可有效幫助學生理清知識的脈絡，確保思路的清晰，同時也能夠完成對數學的概括。

例如，在教學“表面積的變化”時，可以先出示例題：我使用兩個棱長都為一厘米的小正方體將其拼接成為一個長方體，如何計算這個長方體的表面積和體積？并將其與之前的小正方體展開對比。

師：通過剛才的對比，你從中發現了哪些問題？

生1：長方體的體積是兩個小正方體體積之和，但是長方體的表面積為10平方厘米，而兩個小正方體的表面積是12平方厘米。

生2：表面積好像縮小了。可是為什么呢？

師：是呀，這究竟是為什么呢？大家能夠從中發現原因嗎？是否存在規律？

生3：我們可以再使用一個小正方體，將三個小正方體拼接成長方體，然后對比其表面積和體積。

師：這個想法不錯，大家可以試一試。

生3：拼接之后的長方體和三個小正方體的體積之和完全相等，但是表面積仍在縮小。

生4：我們在對比時發現，如果是兩個小正方體進行拼接，它的表面積減少2平方厘米，但是使用三個小正方體進行拼接的過程中，表面積少了4平方厘米。

生5：在拼接兩個小正方體的過程中，有兩個面是重合的，但是在拼接三個小正方體時，有四個面重合在一起。

師：這一點總結得非常好，那么我們接下來拼接六個小正方體。首先看一看這六個正方體可以拼接成幾種不同的長方體？然后，進行對比，看一看哪種表面積最小并說明其原因。

學生們經過自主操作提煉出兩種不同的方法：其一減少了十個面，其二減少了十四個面。很顯然第二種方式的表面積更小一些。

師：那么接下來我們繼續討論導致表面積減少的原因是什么。

學生根據所拼接的實物，展開全方位的觀察和分析，并思考其中的原理。

生6：因為在實際拼接的過程中存在面的重合，只要數一數重合面的數量就能夠知道表面積減少的部分。

生7：當兩個小正方體進行拼接時，減少的只有兩個面，使用三個小正方體是減少了四個面……

生8：根據這個規律可以發現，每次拼接都會出現面的重合，而且重合的面減少兩個。

上述教學案例中，教師準確把握了知識的生長點，并組織學生自主拼一拼、說一說，使學生可以立足于實踐完成對規律的梳理和總結，既有效地鍛煉了學生的動手操作能力及分析能力，還有助于培養學生的數學概括能力。

四、在“錯誤處”點撥，深化數學理解

小學生在數學學習的過程中，會經常出現學習錯誤，對于課堂上學生出現的學習錯誤，教師不能夠進行簡單規避，而應該在他們的數學學習“錯誤處”進行點撥，以此促進他們的數學理解，讓學生經歷糾錯、改錯的過程，從而達到高效化教學的目的。

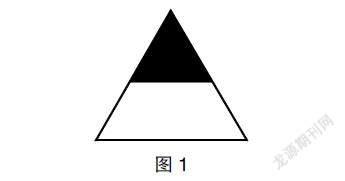
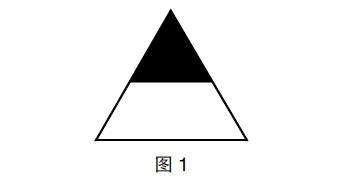
師：同學們，下面這個圖形中的涂色部分用“ ”表示對嗎？

生：不對。因為沒有平均分成2份。

師：那么這個圖形中的涂色部分能不能用分數表示呢？

生1：不能。

生2：是的。因為沒有平均分，肯定是不能用分數表示的。

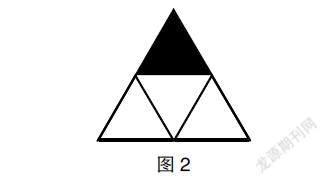
師：如果我在這個圖形上加兩條線，你們看看還能不能用分數表示？

生3：可以的。可以用“ ”表示。

師：現在怎么又可以了呢？

生3：因為這樣看是把這個三角形平均分成了4份，涂色部分占了一份。

生4：看來我們碰到這一類圖形時，還要仔細思考是不是真的沒有平均分。

生5：其實，很多圖形從表面上看沒有平均分，實際上是平均分的。因此，我們不能夠簡單地從表面上看能不能用分數表示。

以上案例中，對于學生片面化的理解而導致的錯誤教師大膽地展示出來，并且，通過給三角形添加輔助線的方式讓學生明白一個圖形是不是平均分不能看表面，而應該進行仔細觀察，深入思考。只要找到平均分成了幾份，就能夠用分數表示。這樣，學生對分數的本質意義的理解也就更加深刻了。在這個過程中，學生有效地把握了數學學習方法。

總之，在發展數學知識以及能力的過程中，需要經歷一個緩慢的遞進過程，需要教師立足于教學實踐，為學生營造有利于其展開思考和體會的良好氛圍，而且應當將慢藝術靈活地運用其中，只有這樣，學生才能夠和數學知識之間展開深度高效的對話，才能有效梳理知識脈絡，高效習得知識。