考查學科本質，引導教學回歸

【摘 要】2021年是部分省份進入新高考的第一年，文章以2021年全國新高考數學Ⅰ卷為例，分析試題命題特點，并從部分試題中探析高考的考查旨意，為新課程的高考改革提供良好的導向。

【關鍵詞】數學試題;新高考Ⅰ卷;學科本質;教學回歸

【作者簡介】丁益民，高級教師，新青年數學教師工作室創始成員，主要研究方向為高中數學教學。

2021年是部分省份高考改革后文理合卷的第一年，教育部考試中心命制的2021年全國新高考數學Ⅰ卷（以下簡稱2021年新高考Ⅰ卷）供江蘇、山東、湖北等地使用，試題從高考數學評價體系出發，秉承重基礎、重本質，貼近高中數學教學實際的命題思路，在全面考查基礎知識和基本技能的同時，貫徹“五育”并舉的教育方針，聚焦數學核心素養與關鍵能力，以基礎性、綜合性、應用性、創新性為導向，突出理性思維的考查。同時，還充分汲取了往年高考數學試卷在命題上的新思路，穩中有變，變中有新，體現出較強的區分度和選拔功能，對推進新高考綜合改革，引導中學數學教學都將起到積極的作用。

一、試題特色

與2008年出臺的高考方案下的江蘇卷相比，2021年新高考Ⅰ卷題型更為豐富（增設單選題、多選題、一題兩空的填空題），與2020年新高考Ⅰ卷和2021年1月的“八省”適應性考試題型一致。與2020年新高考Ⅰ卷相比，2021年新高考Ⅰ卷多選題的賦分規則從少選得3分變為少選得2分，試卷沒有出現結構不良的試題，這與2020年10月中共中央、國務院《深化新時代教育評價改革總體方案》提出的穩步推進高考改革，構建引導學生德智體美勞全面發展的考試內容體系，改變相對固化的試題形式，增強試題開放性精神相一致。試卷應用題背景簡潔明了，沒有冗繁的文字表達，將命題的注意力集中在考查學生解決數學問題的素養上，體現了數學教育應有的務實作風。

從試題結構看，2021年新高考Ⅰ卷考試內容及其分布科學合理，體現了文理不分科后數學考試的特點和內容要求。試卷的選擇題、填空題、解答題起點低、入口寬，面向全體學生，注重對通性通法和數學思想方法的考查。

從試題的難度看，2021年新高考Ⅰ卷重視難度和思維的層次性，如第8、11、12、16題，試題的難度設計不僅具有層次性，還重視數學試題的綜合性、創新性。在思維的靈活性、深刻性，方法的綜合性、探究性和創造性等方面，科學把握試題的區分度，力求發揮數學試題的選拔性功能，如第21、22題，為全面推進新高考改革鋪路，使其循序漸進地過渡下去。

從試題的功能看，在深化課程改革與高等教育大眾化、普及化的大背景下，新高考數學試題既要關注高校對人才的選拔要求，又要關注數學在人才培養中的作用。同時，新高考試題為數學教學改革也提供了教學組織和實施的方向，發揮了高考試題應有的教學導向功能。

二、試題剖析

（一）重視對教材內容把握程度的考查

在當前的教學中，重結論輕過程的現象比較普遍，為了改變這樣的教學現狀，試題從教材出發，回歸知識本原，揭示知識的形成過程，以達到重視教材，重視概念教學的導向作用，比如第10題。

無論是課程標準還是教材，都建議充分發揮單位圓的作用，借助單位圓的幾何直觀，選擇不同的方式推導兩角和與差的正弦、余弦公式，利用向量數量積推導公式是重要的方法之一。本題實質就是運用單位圓上的點及數量積的坐標運算推導兩角和的正弦、余弦公式，高考題的結構與教材（如新人教A版高中數學必修第二冊第35頁例12）這部分內容完全對接，呈現方式與解題過程也與新教材一脈相承。由此可見，試題旨在引導教師重視對知識發生過程的教學，將重心放到知識的生成中，而不是用單純解題活動代替知識的理解。這是利用高考命題的導向功能推動新課程背景下的課堂教學改革，引導廣大教師要關注課程標準，研究教材，重視知識的過程性教學，引導教學回歸知識本原，厘清知識的來龍去脈。

（二）重視從情境中抽象出概念本質的考查

《普通高中數學課程標準（2017年版2020年修訂）》明確指出，在問題解決的過程中，理解數學內容的本質，促進學生數學學科核心素養的形成和發展。2021年新高考Ⅰ卷強調情境的作用，要求學生能從情境中抽象出概念并運用所學知識進行理解與運用，如第8題、第16題均屬于這類試題。下面以第8題為例。

有6個相同的球，分別標有數字1，2，3，4，5，6，從中有放回的隨機取兩次，每次取1個球。甲表示事件“第一次取出的球的數字是1”，乙表示事件“第二次取出的球的數字是2”，丙表示事件“兩次取出的球的數字之和是8”，丁表示事件“兩次取出的球的數字之和是7”，則（ ?）

A.甲與丙相互獨立 ?B.甲與丁相互獨立

C.乙與丙相互獨立 ?D.丙與丁相互獨立

情境是高考評價體系中的考查載體，本題的問題情境是典型的隨機現象實例，考查基本概念“事件的相互獨立性”。舊教材中將“事件的相互獨立性”作為條件概率的后續概念，采用演繹推理的方式得到事件相互獨立的定義，而新教材對此進行了重構——先給出兩個“探究”實例，再利用歸納推理獲得概念，最后通過正、反例對概念的本質進行雙向理解。在概率教學中，教師要結合實例展開，將概念理解置于具體情境中。教材為我們提供了豐富的典型隨機現象實例，如游戲中的隨機現象（拋擲硬幣、拋擲骰子、抽取撲克牌等），生活中的彩票、出生年月、摸球抽簽等隨機現象，實際應用中的隨機抽樣、保險問題、投資理財等，這都是設置問題情境的較好素材，給學生提供了深度學習和思考的空間。在新舊教材過渡階段，教師要走出舊教材的思維定式，加強對新教材的理解和使用。

（三）重視對基本活動經驗的考查

新課程標準明確指出，教學中要引導學生理解基礎知識，掌握基本技能，感悟數學基本思想，積累數學基本活動經驗，促進學生數學學科核心素養的不斷提升。高考題通過典型模型測試學生對核心概念、方法、觀念的掌握，考查學生的“四基”“四能”。如第19題。

記△ABC的內角A，B，C的對邊分別為a，b，c。已知b2=ac，點D在邊AC上，BDsin∠ABC=asinC。

（1）證明：BD=b;

（2）若AD=2DC，求cos∠ABC。

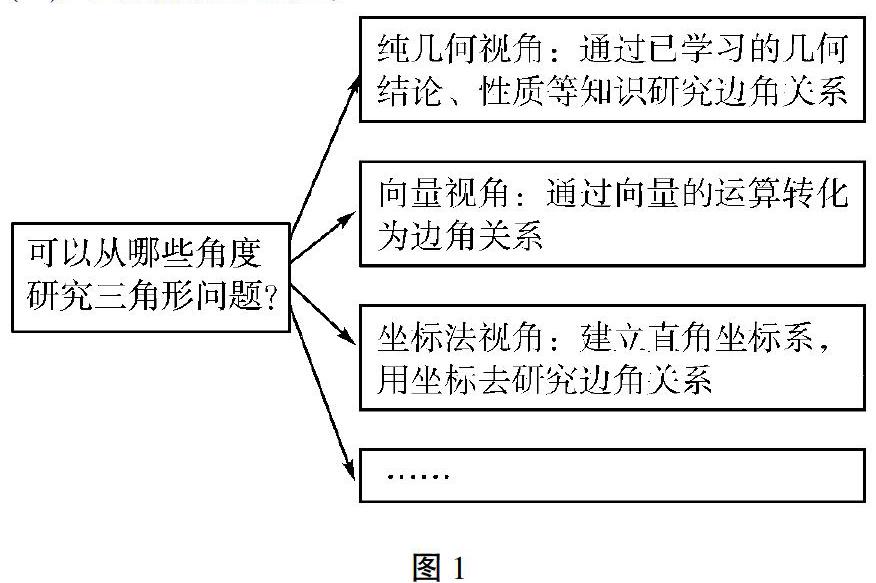
這道題考查學生運用向量，以及正弦和余弦定理等研究三角形的邊角問題，入口較寬，能測試出不同思維水平學生解決問題的能力差異。在“解三角形”的教學中，筆者認為應以三角形為基本幾何圖形，逐步讓學生建立起解決幾何問題的研究系統（如圖1），使得學生形成解決幾何問題的基本思路，以此促進關鍵能力的形成[1]。在教學正弦和余弦定理時，證明的多維視角是解決這道高考題第（2）問的直接示范。

由此可知，只有在教學中不斷引導學生感受上述研究系統，運用這樣的大觀念解決問題，才能形成研究幾何問題的基本范式，進而積累基本活動經驗。一旦有了活動經驗的引領，學生的數學學習才成為有目的、有方向的活動，從而才能從容應對這類高考題。

（四）重視關鍵能力的考查

關鍵能力是學科核心素養的重要載體，學科關鍵能力的培養對形成學科核心素養至關重要，2021年新高考Ⅰ卷圍繞空間想象、抽象概括、推理論證、運算求解、數據處理等關鍵能力展開命題。能力立意一直是高考命題的基本原則，通過試題考查學生綜合運用數學知識和方法分析問題、解決問題的能力，才能形成對考生的科學評價與合理區分[2]。如第21題。

本題著重考查學生的數學運算能力，要求學生在運算過程中合理引入參數，靈活運用運算結構的相似性及對代數式的變形來優化運算，這些都指向于考查學生的綜合素養。能力立意重在考查學生的學習潛能，要求學生對數學有整體的認識，把握數學的整體意義和整體結構，對數學思想方法有較為深刻的領悟與掌握。

三、結語

綜上所述，在平時的教學中，我們要重視回歸學科本原，重視研讀教材，重視理解知識。教師在教學中要讓學生經歷數學概念形成的過程，讓學生理性認識每個概念在整個知識單元（模塊）中的地位與價值。知識的理解不能靠刷題來代替，凡是通過刷題來理解知識的一定不是觸及知識的本質，這樣的理解是膚淺的，也是不可靠的。“反刷題、反套路、反押題”是新高考命題的堅定導向，教師只有在研究新課標、新教材上下功夫，才能引導學生在數學活動中領悟知識的本質，體悟數學思想方法，積累基本活動經驗，提升學生的數學核心素養，科學應對新高考。因此，在教學中要突出知識的過程性理解，重視引導學生在學習過程中積累用數學的眼光觀察、用數學的思維分析、用數學的語言表達的活動經驗，關注數學核心素養的達成。

參考文獻：

[1]丁益民.“解三角形”教學設計中幾個環節的思考[J].中國數學教育，2015（11）：15-17.

[2]劉春艷.數學高考改革的“能力立意”：基于高考試題變化的解析[J].中小學管理，2017（9）：11-13.

（責任編輯：陸順演）