在核心素養背景下的“數的運算”教學探究

黎益

【摘要】本文以人教版小學數學教材為例，論述在核心素養背景下開展“數的運算”教學實踐，提出“把握教材脈絡，厘清‘數的運算知識結構;聚焦教材內容，明確‘數的運算教什么;立足核心素養，確定‘數的運算怎么教”等教學策略。

【關鍵詞】核心素養 運算能力 人教版教材

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2021）25-0066-04

“數與代數”是小學數學教學的重要內容，而“數的運算”內容又在“數與代數”中占較大比例，貫穿于整個小學數學的教學過程。《義務教育數學課程標準（2011年版）》明確指出，在數學課程中，應當注重發展運算能力。因此，教師要重視“數的運算”教學，并且在核心素養背景下聚焦小學數學學科素養的要求，明確“教什么”和“如何教”。本文從整體把握“數的運算”教學內容和結構出發，明確“數的運算”應該是教“意義”、教“算理”、教“算法”，且從“意義理解、理法結合、技能訓練”等方向提出具體的教學策略，以切實提高學生的運算能力，發展學生的學科素養。

一、把握教材脈絡，厘清“數的運算”知識結構

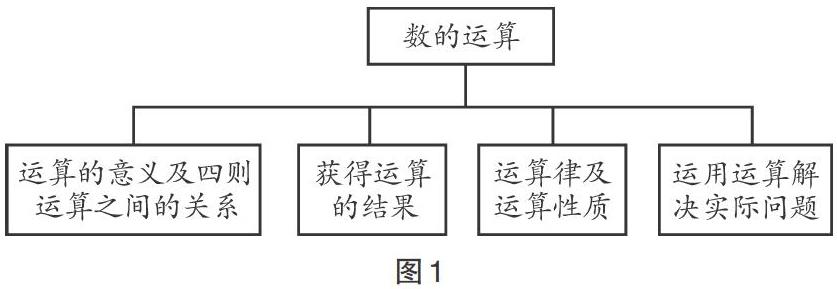
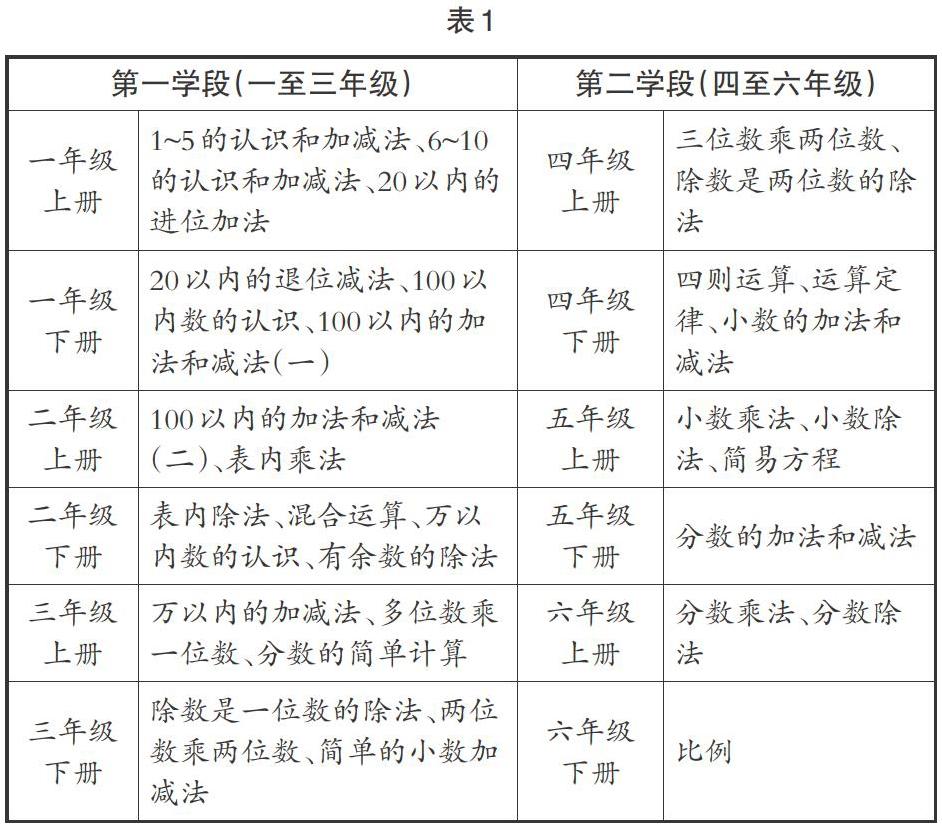
在教學內容體系上，人教版小學數學教材中的“數的運算”包括以下幾條主線：“數的運算”的意義及四則運算之間的關系、獲得運算的結果、運算律及運算性質、運用運算解決實際問題等。（如圖1）而具體的內容在各年級的單元編排如表1所示。

從觀察表1可知，小學人教版教材數的運算是先教整數的四則運算，然后將運算逐步擴展到分數和小數，教材編排上遵循著同一知識“螺旋式上升”、不同知識“交替式增長”的特點，這樣教材就出現了不同的知識單元。因此，教師不能只關注本冊教材，應該走出本冊教材，從知識體系的角度看清同一知識在不同年級的安排，從整體上把握知識之間的內在聯系，才能對本冊教材知識做出準確的定位，進而更加合理地設計教學目標和教學活動。

二、聚焦教材內容，明確“數的運算”教什么

厘清教材中“數的運算”知識結構與內容，才好確定課堂教學需要“教什么”。筆者認為，進行“數的運算”，關鍵是教“意義”、教“算理”、教“算法”。

（一）教“意義”

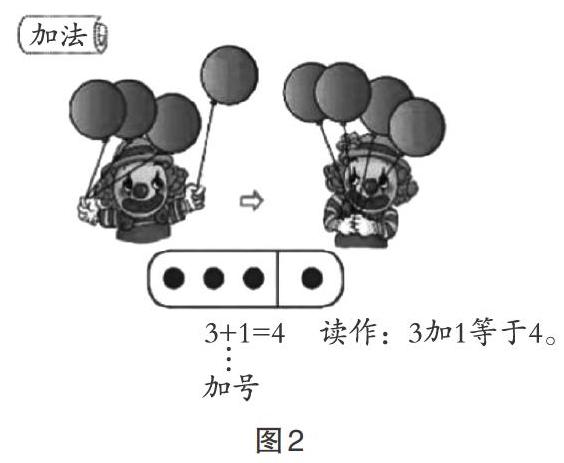
“運算”是根據一定的數學概念、法則和定理，由一些已知量通過計算得出確定結果的過程，而“意義”就是每種運算的本質。人教版小學數學教材中兩次出現“加法的意義”內容，第一次出現是在一年級上冊，第二次出現是在四年級下冊，教材圖例如圖2、圖3（見下頁）。

一年級上冊教材先出示了小丑右手拿3個紅氣球、左手拿1個藍氣球，雙手合起來拿是4個氣球;然后3個紅氣球用3個圓點表示，1個藍氣球用1個圓點表示，4個圓點對應表示紅藍氣球合并的圖例;接著出示3+1=4這個加法算式，引出“加號”。三個環節從具體情境的動作表征到符號表征，再到算式表征，展示了從具體到抽象的演變過程，同時揭示了“把兩個部分合起來就用加法”，幫助學生第一次建立加法的意義概念。

在學生經過幾年的數學學習之后，四年級下冊將“四則運算”作為一個獨立的單元進行教學。以加法為例，教材中先呈現“西寧到拉薩的鐵路長多少千米？”的問題情境，然后從線段圖轉換到加法算式“814+1142=1956”，再揭示加法的意義是“兩個數合并成一個數的運算”。教材根據學生認知特點，在低、中學段都呈現關于加法意義的教學內容，通過不同的表征讓學生由初步認識到明確加法的意義。同樣的，關于減法、乘法、除法的意義，教材也是這樣編排教學內容的。

（二）教“算理”

算理是計算的道理、想法，主要解決“為什么要這樣算”的問題。人教版小學數學教材中很清晰地編排有關于算理的內容，如一年級下冊“兩位數加一位數和整十數”，教材圖例如圖4。

教材先對比出示“25+2”和“25+20”兩個算式，然后借助小棒模型，讓學生直觀地觀察“25+2”中的5根小棒和2根小棒合并在一起，“25+20”中的2捆小棒和2捆小棒合并在一起，接著將口算的過程與擺小棒的過程相對應，引導學生認識“把5個一和2個一先合起來，其實就是先算5+2”，“把2個十和2個十先合起來，其實就是先算20+20”，進而理解“相同的計數單位相加”的道理。

（三）教“算法”

算法就是實施四則運算的基本程序和方法，主要解決“怎樣計算”的問題。在教材中我們常常可以看到這樣的小組討論情境，“計算萬以內的加法要注意什么？”“多位數乘一位數的乘法怎樣計算？”等問題（如圖5），這其實就是在學生理解算理之后，促進他們以小組討論的方式進行交流，然后師生共同總結算法的過程。可見，算法是“數的運算”教學中必須要重視的內容。

三、立足核心素養，確定“數的運算”怎么教

“數學運算”是數學活動的基本形式，是獲得數學結果的重要手段，也是數學學科六大核心素養之一。在當前核心素養的背景下，學生關鍵能力發展備受關注，因此教師要重視學生運算能力的培養。在教學中，筆者認為可以從“意義理解、理法結合、技能訓練”三方面實施“數的運算”教學。

（一）意義理解

理解運算的意義，即能描述運算的特征和由來，闡述不同運算之間的區別和聯系。

【案例描述】四年級下冊《除數是整十數的筆算除法》

師：同學們平時應該都有在做一些體育運動，而做某些運動是需要借助體育器材的。請看書本，體育老師正在分發運動器材呢，誰能說說自己看到的數學信息？

生1：我看到體育室有60個呼啦圈、92個毽子、140根跳繩。

提出問題：60個呼啦圈，每個班30個，可以分給幾個班？

生2：60÷30=2，可以分給2個班。

師：為什么用除法解決這個問題？你是怎樣計算得出答案“2”的？

生2：這道題其實是要求算出60里面有幾個30，所以用除法計算最快得出答案。

師：現在體育老師還要對毽子進行分配，你們能提出什么問題？

生3：現共有92個毽子，每班30個，可以分給幾個班？

師：用什么方法解決這個問題？能列出算式嗎？

生3：92÷30=

師：為什么還是用除法？（生說師板書）

生4：問“可以分給幾個班”，就是要求算出92里面有幾個30，所以用除法計算。

在教學本課之前，學生已經學習了除數是整十數的口算除法，所以在本課的開始，學生很快通過口算得出60個呼啦圈，每個班30個，可以分給2個班，即60÷30=2。在此基礎上，教師追問“為什么用除法解決問題？60里面有幾個30？你是怎樣算的”，把學生的思維從單純的口算轉向對算式意義的理解和對算理的思考，接著學生練習提出問題“92個毽子，每班30個，可以分給幾個班”，筆者追問“為什么還是用除法解決”，讓學生在提出問題、解決問題的過程中進一步理解除法的意義。而在“數的運算”教學中，問題解決與計算教學常常聯系在一起，借助具體的問題情境，教師多問一句“為什么用加（減、乘、除）法解決這個問題”，能引導學生將生活問題數學化，加深對運算意義的理解。

（二）理法結合

理法結合，即將算理和算法有機融合，由算理直觀化過渡到算法抽象化，在理中形成法，在法中蘊含理，實現明白地算。

【案例描述】四年級下冊《小數的加減法》

1.談話引入

教師板書“215+3”，然后提問“這道題你會算嗎？請用豎式記錄計算過程”。

師：為什么要相同數位對齊呢？（出示計數器進行解釋，3是3個一，與個位的5個一相加得8個一，也就是個位與個位對齊，5+3=8，相同計數單位的數相加）

2.改題導入

這兩個數分別添上小數點（2.15+0.3），揭示課題“小數加減法”。

3.獨立思考，初探算法

師：這兩道題你打算怎樣算？用自己的方式解釋為什么這樣算。

4.多元表征，初步詮釋算理

生1：我用計數器撥珠的方法，直接在十分位上撥3顆珠子，結果就是2.45了。（如圖6）

生2：我用的是方格圖，直接把3個長條放在1個長條的下面，結果也是2.45。（如圖6）

生3：我是用人民幣擺的，給這兩個數添上單位“元”，整數部分上的數表示的是元，十分位上的數代表的是角，百分位上的數代表的是分，2元1角5分加3角，就是2元4角5分，也就是2.45元。（如圖6）

生4、生5用的是寫豎式的方法。（如圖7）

師：他們列的豎式計算，你同意嗎？為什么？

分析生5的豎式寫法：0.3的3是十分位的，要跟2.15十分位上的1對齊相加，所以結果是2.45。

5.錯題辨析，抓住本質

分析生4的豎式寫法：0.3中十分位的3與2.15中百分位的5對齊相加得到8，這個“8”是8個十分之一還是8個百分之一？看來計數單位相同的數才能直接相加，計數單位不同的數不能直接相加。所以2.15+0.3的正確結果應該是2.45。（教師板書橫式答案）

6.回顧小結，體驗算法

（1）在解決2.15+0.3的時候，我們用了幾種不同的方法，都是把相同計數單位上的數相加。（板書：相同計數單位的數相加）

（2）說說豎式的計算過程。

7.二次改題，學習小數減法

師將2.15+0.3改為2.15-0.3。提問：為什么豎式中的3要寫在1的下面？

8.加減對比，小結算法

（1）師提問“計算小數加減法時需要注意什么”，引導學生討論、總結。

（2）師提問“我們在計算整數加減法時是末尾對齊，但在小數加減法計算時卻把小數點對齊，看似不同，其實中間隱含著一個共同的道理，是什么呢”，引導學生概括歸納算法經驗。

由這個案例可以清晰地看到，教師是在溝通聯系中引導學生理解算理、掌握算法，實現理法結合。開課時計算“215+3”，教師用計數器呈現計算過程，幫助學生理解“相同數位對齊”，其實就是“相同計數單位的數相加”，這是第一次溝通;然后算式變形“2.15+0.3”，當學生用不同方式解釋自己的算法后，教師利用課件讓學生觀察：解決問題的表達方式不同，但它們具有相同的地方，就是“相同計數單位的數相加”，這是第二次溝通;接著學生自主嘗試計算“2.15-0.3”，教師提示小數減法豎式與小數加法豎式一樣，也要“相同計數單位的數相減”，這是第三次溝通;第四次溝通，是由教師提出問題“我們在計算整數加減法時是末尾對齊，但在小數加減法計算時卻把小數點對齊，看似不同，其實中間隱含著一個共同的道理，是什么呢”，讓學生發現整數加減法與小數加減法之間的聯系與區別。學生經過對比多元表征方式的異同、找圖式的對應之處、溝通新舊知識的連接點與增長點，不知不覺理解了加減法計算的基本道理——相同計數單位的數才能相加減。理解了這一本質，學生對加減法計算的算法自然就掌握了，也為后續學習分數加減法埋下了伏筆。

（三）技能訓練

技能訓練，即通過類題、變式題、對比辨析等多種方式，在完成一定量的訓練后實現正確地算。

【案例描述】五年級上冊《小數乘法練習課》

背景：計算4.3×0.21，要先計算43×21（按整數乘法計算出積），再點小數點，那么師生共同把“43×21”稱為4.3×0.21的“隱形替身”，由此學生舉出很多以“43×21”作為隱形替身的例子，如0.43×2.1、4.3×2.1、0.43×21、0.43×0.21……

師：“43×21”只能作為小數乘法的隱形替身嗎？如果我們要計算430×2100（指著豎式430×2100提問），先計算出“43×21”的積，其實是在計算什么？

生1：是在算計數單位的個數。

師：為什么在積的末尾添上3個0？

生2：為了確定計數單位是1000。

師：看來在小數乘法和整數乘法中，都能用到隱形替身。它們的計算方法看似不一樣，有的添“0”，有的點“·”，為什么要這樣做呢？

生3：它們都是在確定計數單位。

提高學生的運算能力，一定量的技能訓練是必不可少的，但一定是以量取勝嗎？大量的練習就一定能提高計算的正確率嗎？答案是否定的。此案例提供的是一節練習課的教學片段，根據學生的反應可知，練習課不一定要設計大量的機械練習，適量的練習同樣可以幫助學生厘清運算中算理的聯系。“通”則“統”，算理是運算的通性通法。在數學教學中，教師要教給學生的不應僅僅是數學的技能技巧，更重要的是數學中的“通性通法”，讓學生體會數學不是“機械”的，而是講“理”的。

總之，學生運算能力的培養不是一朝一夕的事情，也不是上一節課就可以實現，教師需要站在整體把握教學內容的高度上，明確課堂教學中“教什么”和“怎么教”的問題，才能循序漸進地提升學生的運算能力，促進學生數學核心素養的發展。

【參考文獻】

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2]曹培英.跨越斷層，走出誤區：“數學課程標準”核心詞的解讀與實踐研究[M].上海：上海教育出版社，2017.

[3]吳正憲，張秋爽，李惠玲.和吳正憲老師一起讀數學新課標[M].北京：教育科學出版社，2013.

[4]劉加霞.小學數學課堂的有效教學[M].北京：北京師范大學出版社，2008.

[5]張奠宙，鞏子坤，任敏龍，等.小學數學教材中的大道理——核心概念的理解與呈現[M].上海：上海教育出版社，2018.

【作者簡介】黎 益（1971— ），女，漢族，廣西柳州人，大學本科學歷，高級教師，廣西特級教師，現任柳州市潭中路第二小學教育集團總校長，研究方向為基于核心素養的小學數學教學。

（責編 黃健清）