積淀：從“做中學”到“玩中創”

黃海燕

[摘 要]在合理運用策略解題之前，習得解題的技能、理順解題的思路是基礎。在“多邊形的面積”的教學中，學生能將“轉化”思想內化成自己解決問題的一種策略，說明了解題技能的習得對開拓解題思路大有裨益。

[關鍵詞]學習;主動權;數學思維

一、意外的收獲

蘇教版教材將“多邊形的面積”編排在五年級上冊，對應的單元教學的開始是引導學生探索平行四邊形的面積公式，通過教學意在讓學生初步體會復雜圖形可以轉化成簡單的圖形，其中割補、平移是實現轉化的基本方法——轉化前后圖形的形狀變了但面積不變。

基于對教材的理解，筆者按照教學設計一步步展開，但學生的表現超乎想象。意外的收獲源于一個學生對問題“圖中平行四邊形的面積是多少呢？”給出的獨特想法，他說：“用數格子的方法，可以看到這個平行四邊形是可以填補成長方形的。那么是不是所有的平行四邊形都可以填補成長方形呢？”其他學生對于這個想法的反應十分強烈，馬上比畫起來，還時不時給出回應：能的！可以的！是長方形……

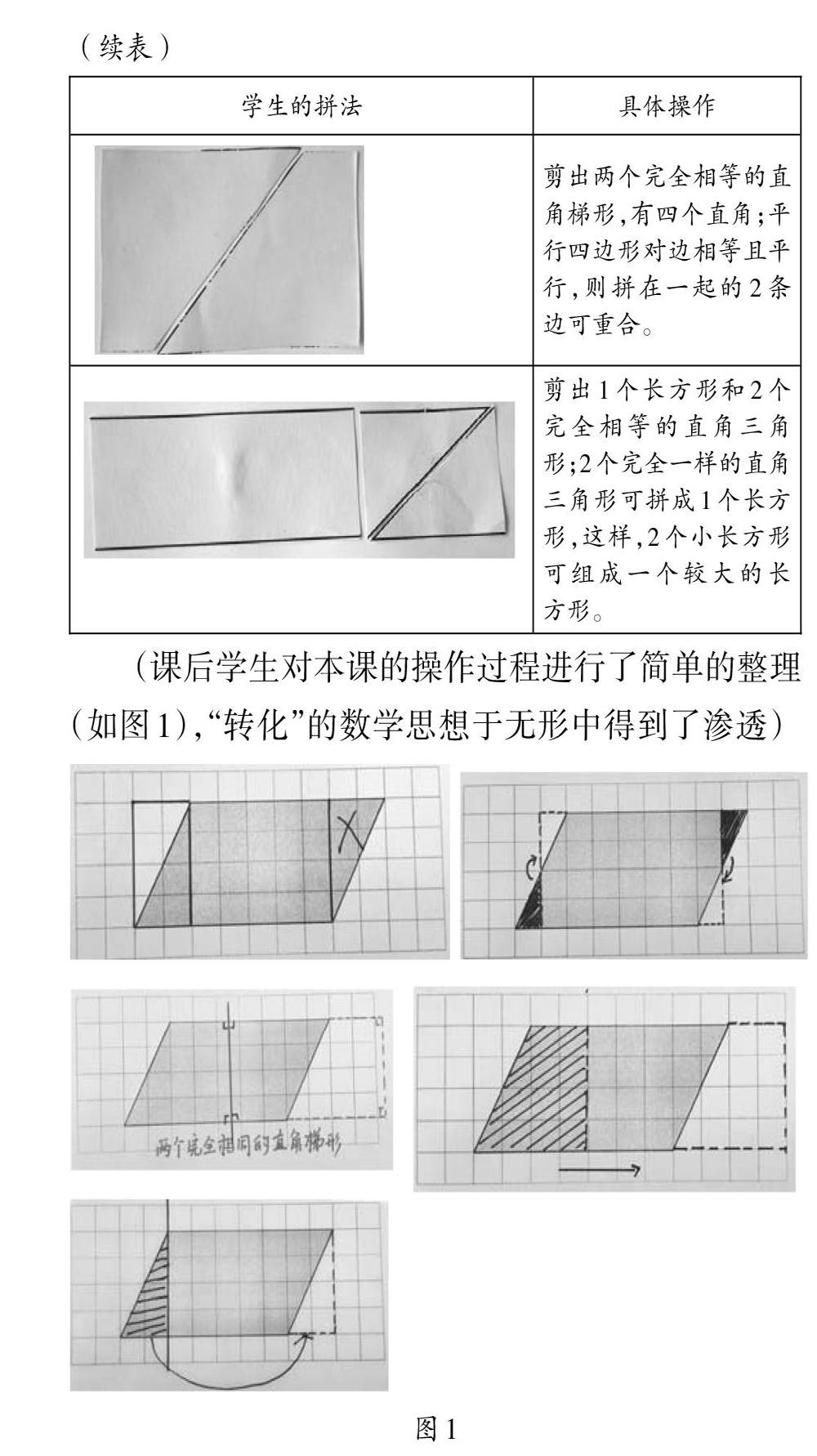
此時的課堂，已經不再適合引入教材上的那一句“你能把右邊的平行四邊形轉化成長方形嗎？”，筆者決定順勢而為，順著學生的話往下走：“既然我們有了猜想，就應該去想辦法驗證。”于是，學生開始了剪、移、拼，用各種方法將平行四邊形轉化成與它面積相等的長方形（如下表）。

是什么改變了原有的教學計劃？準確地說，是什么讓學生“打亂”了教師的設計，成為課堂真正的學習者？源于學生對知識的學習不再是被動的接受式，而是有一種主動探索的欲望和能力。但凡事不會一蹴而就，必是有其長期積累的過程，再形成質的飛躍。

二、量的積淀

課堂教學無疑是一個長期積淀的過程，每一節新課的教學都是一塊奠基石。傳統的課堂模式，更多的是通過“精講多練”以及知識的梳理，達到鞏固知識的目的，但伴隨著時代的發展和實施素質教育要求的提出，學生的動手操作能力、分析能力、創新能力、合作能力以及獨立探究的精神、解決問題的信心等方面也得到了關注和重視。

個人認為，學生通過教師引領、自主探究、交流后習得的解題“策略”，遠比“題海戰”要來得有效。這里的“策略”不僅包括傳統應用題教學中所提到的“數量關系”和“分析方法”，還包括了一些基本能力的培養，如“提出問題”“分析情境”“搜集信息”等。而清晰的解題思路體現學生能明確地圍繞題目進行連貫而合乎邏輯的思維活動過程。

“轉化”思想是建立在學生已有的知識經驗基礎之上的，在具體的情境下進行合理的推想，是獲得數學知識的一種有效手段。正如荷蘭數學教育家弗賴登塔爾所說：“真正的數學家常常憑借數學的直覺思維做出各種猜想，然后加以證實。”作為小學數學教師，在教學的過程中也需重視數學思想方法的滲透，以此增強學生主動探索、獲取數學知識的能力。

1.合理設問，學生敢想

許多數學結論都是從猜想開始的。數學猜想是人們依據已有的數學知識和經驗，運用非邏輯的思維方法，憑借直覺而做出的假設和預測，它是人們探索數學規律，發現數學知識的手段和策略。

在課堂教學中，教師要設置合理的問題情境，引導學生做出大膽合理的猜想，這不僅能夠調動學生學習的積極性和主動性，促使學生主動探索和獲取知識，還有利于培養學生的直覺思維、探索精神和創新意識，從而發展學生的推理能力。

【教學片段1】認識長方形和正方形

師：找一找這幾張不同的彩紙中，哪一個是長方形的？

（學生都能快速找到長方形彩紙，并將其高高舉起）

師：對，這些大大小小的圖形都是長方形。想一想，長方形的邊和角有著怎樣的特征？

生1：長方形的角是直角，邊也是直直的。

生2：我要補充。長方形有4個角，4個角都是直角。長方形的邊有4條，2條長一點，2條短一點。

生3：我可以說得更好。長方形有4個角，且4個角都是直角。長方形有4條邊，都是直直的，且上下2條邊相等，左右2條邊也相等。

師：我把大家的猜想進行整理。

角：有4個角，且4個都是直角。

邊：有4條邊，上下2條邊相等，左右2條邊相等。

師：剛才大家說得都很好。那么長方形的邊和角是不是具有這樣的特征呢？學數學不僅需要大膽猜想，驗證也同樣重要。你能想辦法來驗證剛才的猜想嗎？

……

對于長方形，學生并不陌生，因為不但生活中隨處可見，他們在一年級“認識圖形”中也有所接觸。從“找”到“說”，不但調動了學生已有的生活經驗和知識經驗，學生也能在一次次的交流中猜想出長方形的邊和角的特征。

2.動手實踐，驗證猜想

在探索長方形的邊和角的特征時，學生能依據問題進行合理猜想。在教師并沒有給出太多提示的情況下，學生就能夠通過動手折一折、比一比等方法，驗證自己的猜想，學生這一“驗證猜想”的過程便是學生習得知識的一種內化。

【教學片段2】認識長方形和正方形

生1：我用三角尺上的這個直角在這張長方形的紙上比一比，就可以證明這4個角是直角了。（邊說邊比畫）

師：這是個好方法。

生2：我只要比一個角，就可以證明長方形的4個角都是直角了。

師：你是怎么做到的呢？

生2：我是先對折2次長方形的紙，這樣4個角就重合了，再用三角尺上的直角和重疊的這4個角比一次。

（有一些學生開始模仿生2的方法：先折再比，驗證長方形的4個角都是直角）

師：你們能聽得懂生2的方法嗎？為什么只需要驗證一個角是直角就行了？

生3：因為其他的三個角與第一個角是完全重合在一起的，是一樣大的，所以只要證明其中一個角是直角，那么其他的三個角也是直角。

師：說得真好！因此我們的結論就是長方形的……

生（齊）：長方形的4個角都是直角。

3.方法遷移，玩創數學

數學猜想并不是亂想，需要建立在學生原有知識經驗的基礎之上。當一個較為復雜的問題被提出時，教師應引導學生調動原有的知識，找到新舊知識之間的聯系，憑借“猜想—驗證”創造新知。這一方法的習得，在“圖形與幾何”領域的學習中有著重要的作用。文章開頭學生在探索平行四邊形面積時的表現就是最好的證明。

當數學的思維方式真正扎根于學生，那么在探索“梯形的面積計算方法”時，教師就不需要太多的課前引導，甚至可以直接拋出問題：“大膽猜想，梯形與哪些我們學習過的平面圖形之間是可以互相轉化的呢？小組合作寫出梯形面積計算公式。”

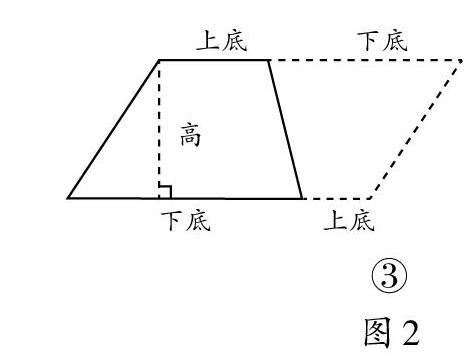
這一次的探索也是成功的。學生能夠得出：①通過割補將它轉化為長方形;②通過割補也可以將它轉化為一個三角形;③構造一個全等的梯形，旋轉后拼成一個平行四邊形……（如圖2）

三、結語

瑞士兒童心理學家皮亞杰將人從嬰兒到青春期的認知發展分為四個階段：感覺運動階段、前運算階段、具體運算階段和形式運算階段。具體運算階段（7～11歲）的兒童思維特征是多維思維、思維的可逆性、去自我中心、具體邏輯推理。因此在小學階段，學生對符號、運算性質的推理可能會感覺到困難，而對直觀圖形的理解就容易得多。

“猜想—驗證”思想方法就可以從小學數學階段的“圖像與幾何”領域開始滲透，讓學生在問題提出之后思索、聯想→假設、猜想→操作驗證結論。而操作方式可以是折一折、畫一畫、涂一涂、比一比等直觀行為，這些更易被學生理解和運用。

從“做中學”到“玩中創”，課堂之所以會越來越精彩，那是源于課堂中每個鮮活的個體，只要在學生心中種下一顆思維萌芽的種子，細心澆灌與培植，相信必將迎來綠意盎然的春天！

[ 參 考 文 獻 ]

[1] 劉健.《解決問題的策略》教學設計與評析[J].小學教學研究，2008（05）.

[2] 王希銀.如何培養小學生的數學猜想能力[J].教育教學論壇，2011（24）.

[3] 童正香.例談新課程理念下小學數學猜想教學[J].中國校外教育（基教版），2009（6）.

[4] 中華人民共和國教育部.義務教育數學課程標準（ 2011年版）[M].北京：北京師范大學出版社，2012.

[5] 劉國權.小學教育心理學[M].北京：人民教育出版社， 2003.

[6] 馬云鵬.小學數學教學論[M].北京：人民教育出版社，2003.

[7] 江丕權.解決問題的策略與技能[M].北京：科學普及出版社，1992.

[8] 蔣明玉.“猜想—驗證”在小學數學教學中的運用[J].小學教育科研論壇，2003（10）.

（責編 童 夏）