《幾何畫板》與數學課堂教學整合的實踐與思考

丁孫順

摘 要：信息技術和智慧教育現已廣泛的應用于數學課堂教學中，《幾何畫板》因其靈活的繪圖、簡潔的圖形展示、強大的數形結合功能，已成為中學數學教師進行信息技術與數學教學整合的首選軟件。中學數學教師教學中需要不斷探究幾何畫板的基本功能，并因勢利導的結合課堂教學和學生學習的實際需要，切實提升教學教學的質量. 本文主要從教學案例出發，談如何更好實現幾何畫板與數學課堂整合

關鍵詞：幾何畫板;初中數學;整合

教育部在全國中小學信息技術教育工作會議上指出：“要努力推進信息技術與學科教學的整合，鼓勵在學科的教學中廣泛應用信息技術手段，并把信息技術教育融合在學科的學習中。”《幾何畫板》軟件的出現，豐富了傳統的數學教學方法，為數學教學注入了新的活力。《幾何畫板》因其靈活的圖形繪制、強大的數形結合功能，不僅能方便學生對數學問題的理解，還能引導學生利用它去進行探索和創新。在此，筆者將基于自己的教學實踐，談一談《幾何畫板》與數學課堂教學整合的思考

一、揭示圖形內在聯系，激發學生學習興趣

初中的基本平面幾何圖形如三角形，四邊形，圓之間，存在較多的內在的關聯。限于黑板的功能限制，老師難以向學生充分展示圖形之間的特點。合理的使用幾何畫板的動態演示功能，可以直觀展示隱藏的圖形信息，使得數學課堂充滿“趣味”和“神奇”。例如在《圓》這一章的起始課中，要體現圓的廣泛存在性，及與其他基礎圖形的關聯，老師可以利用幾何畫板軟件設計數學實驗，引導學生動手操作發現。

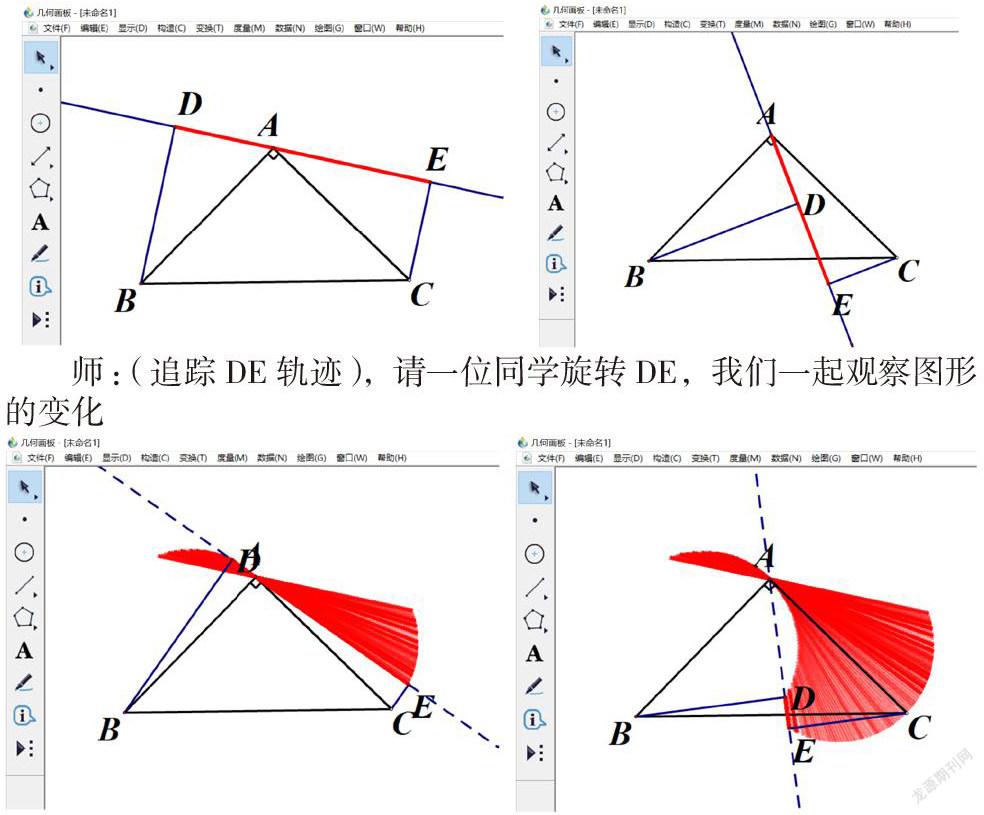
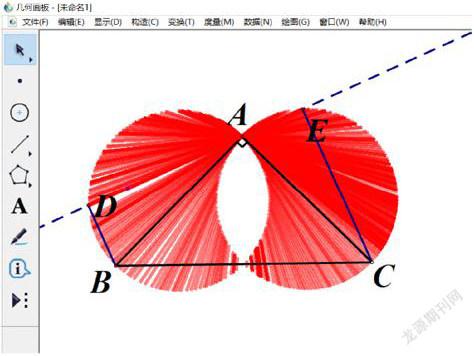
師：在《全等三角形》中，我們接觸到了一線三等角模型，如圖，直線DE繞點等腰RT△ABC頂點A旋轉過程中，我們能得到DE=DB+EC或DE=DB-EC，那么在直線DE旋轉的過程中，會不會有圓的產生、出現呢？

師：（追蹤DE軌跡），請一位同學旋轉DE，我們一起觀察圖形的變化

生：（驚奇的）有兩個等圓出現了

師：圓隱藏在很多基礎圖形中，他和這些基礎圖形之間聯系緊密。實驗中大家發現的現象，我們將在《圓》這一章中將得到很好的解釋，從今天開始，就讓我們一起走進圓的世界。

以上幾何畫板展示的現象其實是圓的定義的表現，同時也體現出了圓于直角三角形的關聯，和本課的主題聯系緊密，激發了學生學好本章的熱情。

二、體現數形結合思想，明晰函數圖像性質

函數是初中代數學的重要組成部分，他是從數量關系的角度描述運動變化規律的數學概念。初中學生的抽象思維能力較弱，如何讓他體驗和理解函數的圖象和性質之間的關聯呢？借助幾何畫板軟件，我們就可以將這個問題得到很好的解決。

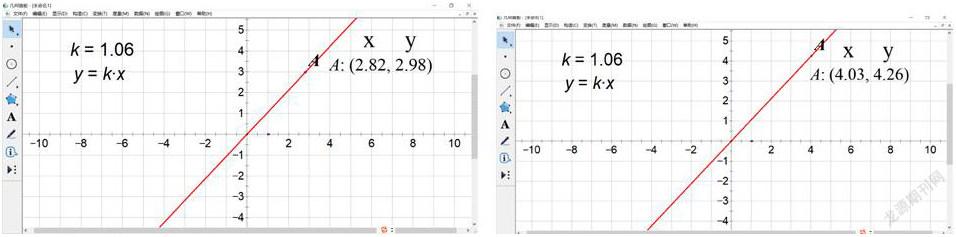
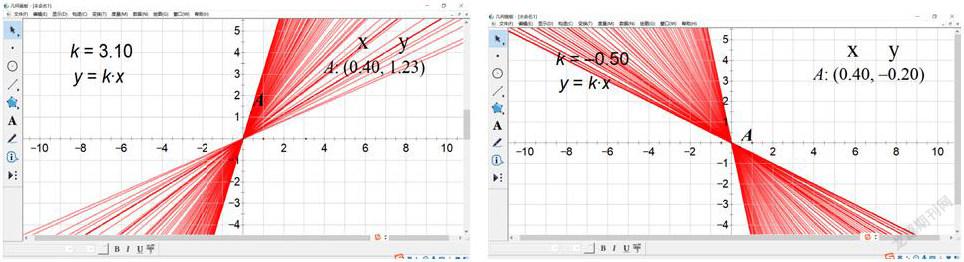
例如，在《正比例函數》一節中，根據教程要求，學生需要從較少的圖像案例中歸納函數圖像特點及其增減性，這對初次接觸函數的學生來說有不小的認知難度，教師可以安排以下的操作環節，隨機改變參數k取值，觀察圖形特點

師：我們可以根據K的大小，對正比例函數圖像進行分類嗎？

生：可以，我發現K取正值或負值，對正比例函數圖像特點不同，故而可以分成兩類

師：很好，K取正值時，我們描述圖像為自左向右上升

K取負值時，我們描述圖像為自左向右下降，

師：那么圖像上升時，變量y，x有怎樣的關系呢？請觀察以下演示實驗，準備好總結歸納

生：圖像上升時，變量y隨x的增大而增大

師：那么圖像下降時，變量y，x有怎樣的關系呢？你有何猜想

生：圖像上升時，變量y隨x的增大而減小

師：同學們歸納的很好

通過教師在幾何畫板上的動態演示，學生直觀的感受了正比例函數的圖象的特點，形成了深刻的印象，同時，幫助學生進一步認識到函數的數量變化關系和函數的圖像是有關聯的。

三、發揮精確測量功能，輔助證明經典定理

在初中教材中，很多經典定理的證明作為拓展內容，安排在其中。對于這部分定理的理解和證明有助于學生了解知識形成的過程，也有助于提升發現和思維能力。

例如，勾股定理在很多教材中都介紹了幾何原本中的經典證明方法。如何引導學生理清整理的思路和方法呢？幾何畫板的精確度量功能，可以為證明提供線索和方向

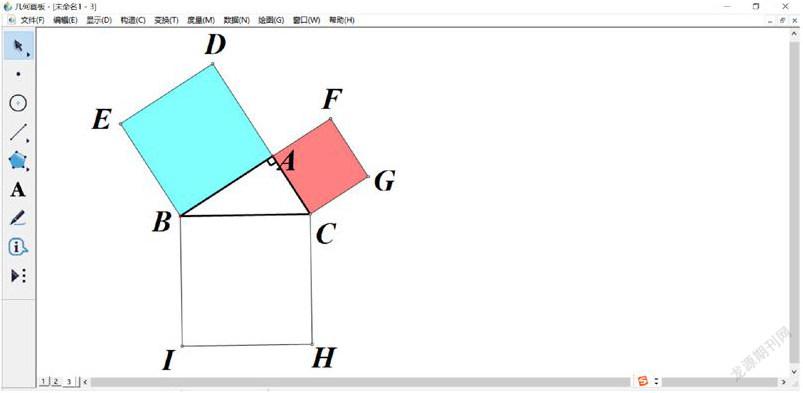
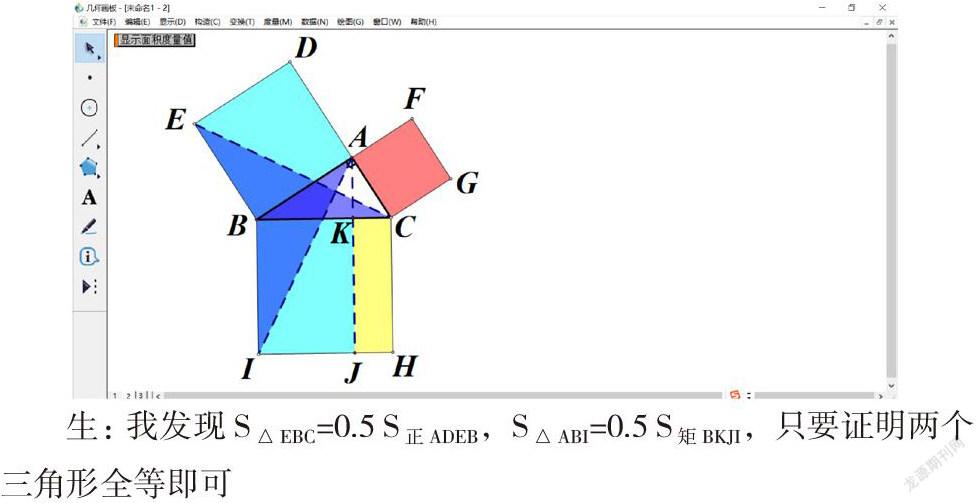
師：RT△ABC向形外各做出正方形，我們探究三個正方形之間的大小關系。（畫板操作：A點做IH的垂線，將最大的正方形分割為兩個矩形）請大家先猜想，兩個矩形和兩個較小的正方形面積有什么關系？

生：兩個矩形和兩個較小的正方形面積對應相等

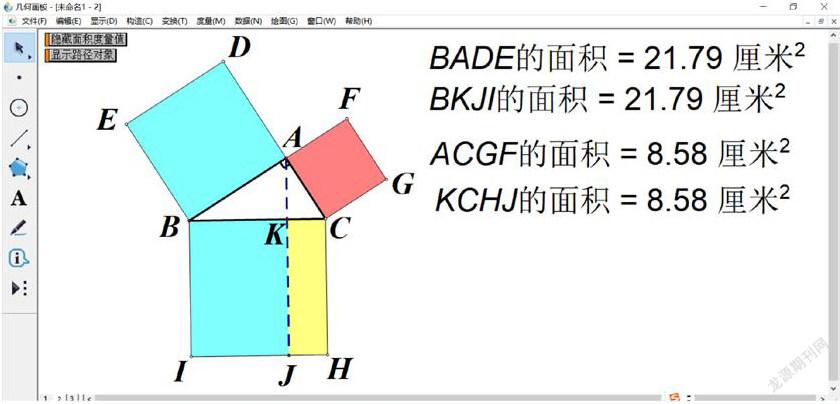
師：我們用幾何畫板檢驗下同學們的猜想

師：猜想如何證明呢？我們可以考慮將以上矩形、正方形面積的轉化同底等高的三角形面積問題

生：我發現S△EBC=0.5 S正ADEB，S△ABI=0.5 S矩BKJI，只要證明兩個三角形全等即可

師：這個發現很重要，請同學們完成證明

很多經典的數學定理都以猜想為基礎，利用幾何畫板的測量功能，能驗證猜想的正確性，進而完成進一步的推理和證明。 這充分體現了在數學探究中實踐可以作為理論的先導，幾何畫板可以很好的幫助我們完成這些實驗工作。

四、展示動點運動軌跡，培養學生動態思維

中學很多數學問題都在鍛煉學生在變化的圖形（數量）中抓住本質規律的能力。這需要學生要用動態思維考慮問題，并能靜心進行歸納總結，進而解決實際問題。

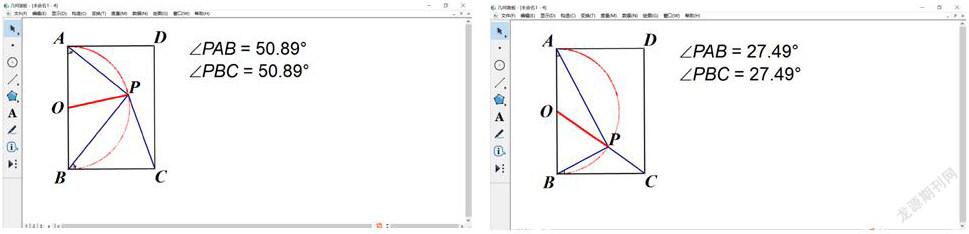
例如：如圖，在矩形ABCD中，AB=8，BC=5，P是矩形內部一動點，且滿足∠PAB=∠PBC，則線段CP的最小值是（ ?????）

師：從這一題的主要條件∠PAB=∠PBC，你能推得其他角度信息嗎？

生：根據等式性質還能得到∠APB=90°

師：動點P滿足∠APB=90°，他會以怎樣的軌跡運動呢？

生：根據圓周角知識，我猜想P點的軌跡為圓弧

師：我們來驗證猜想

（動態追蹤P的軌跡）

師：動點P的軌跡是以AB為直徑的圓弧，為什么會出現這種軌跡，能用學過的知識進行解釋嗎？

生：取AB得中點O，連接OP，根據斜邊中線等于斜邊的一半，所以，OP長度為定值 ，P的軌跡為以O為圓心，OP長為半徑的圓弧

師：回答的很好，那么動點P運動到何處時，PC最短呢？

請再觀察幾何畫板的演示

生：P于O、C三點共線時PC最短

借助于《幾何畫板》的演示，學生在圖形變化的過程中去觀察、比較、歸納、總結圖形的規律，既增強了學生學習幾何的興趣，提升了學生的數學思維品質。

綜上，《幾何畫板》的使用能更好實現數學課堂教學與信息技術的整合，能更好學生在學習過程中的主體作用和教師的主導作用。《幾何畫板》的各種演示實驗，讓學生去觀察、猜測、歸納、驗證從而得到正確的結論，充分展示了知識的形成過程，教師不再是簡單的知識“灌輸者”，而是學生獲取知識的引導者，學生也不再是簡單的知識接受者，而是獲取知識的探索者.在這里，學生主動參與到數學活動中，自主探索，親自去體驗、嘗試，從而激發了學習興趣。

《幾何畫板》軟件輔助數學課堂教學，提高了教學效率、培養了學生的想象能力和圖形理解能力，真正實現了讓圖形（數量）在學生的頭腦中“動”起來。

參考文獻：

[1]吳桐.幾何畫板與初中數學教學整合的實踐與研究[D].武漢：華中師范大學，2017.

[2] ?王巖，陳廣.幾何畫板與初中數學教學整合的實踐探索[J].中國教育技術裝備，2016（19）：11-12.

[3] ?沈忠良.幾何畫板與初中數學教學整合的實踐應用[J].課程教學研究，2015（11）：64-67.