雙減背景下初中數(shù)學(xué)作業(yè)設(shè)計(jì)的實(shí)踐

蔣柏平

摘要：“雙減”政策要求減輕義務(wù)教育階段學(xué)生作業(yè)負(fù)擔(dān)，而作業(yè)又是學(xué)生課堂內(nèi)容掌握程度的重要反饋，因此教師的作業(yè)設(shè)計(jì)就顯得尤為重要。本文結(jié)合《矩形、菱形、正方形（第1課時(shí)）》的作業(yè)設(shè)計(jì)，從引導(dǎo)先學(xué)、鞏固所學(xué)、因需布置、切合考試四個(gè)方面談?wù)勛鳂I(yè)設(shè)計(jì)的思路，力求體現(xiàn)作業(yè)設(shè)計(jì)的前瞻性、鞏固性、層次性和高效性。

關(guān)鍵詞：雙減;初中數(shù)學(xué);作業(yè)設(shè)計(jì)

中圖分類號(hào)：G4 文獻(xiàn)標(biāo)識(shí)碼：A

初中數(shù)學(xué)是義務(wù)教育階段的必修學(xué)科。作業(yè)是教學(xué)的重要環(huán)節(jié)，是課堂教學(xué)的重要延伸，不僅僅體現(xiàn)在對(duì)所學(xué)知識(shí)的復(fù)習(xí)、鞏固、內(nèi)化，更體現(xiàn)在促進(jìn)學(xué)生核心素養(yǎng)的發(fā)展[1]。“雙減”政策要求減輕義務(wù)教育階段學(xué)生作業(yè)負(fù)擔(dān)，因此好的作業(yè)設(shè)計(jì)就顯得尤為重要。筆者通過《矩形、菱形、正方形（第1課時(shí)）》這節(jié)課的作業(yè)布置實(shí)踐，談?wù)勲p減政策下作業(yè)設(shè)計(jì)的思路。

一、引導(dǎo)先學(xué)，作業(yè)設(shè)計(jì)為新課講授做鋪墊，突出作業(yè)布置的前瞻性

預(yù)習(xí)作業(yè)是學(xué)生課前準(zhǔn)備的一個(gè)重要環(huán)節(jié)，古語有云：“凡事預(yù)則立，不預(yù)則廢”。好的預(yù)習(xí)作業(yè)可以激發(fā)學(xué)生自主預(yù)習(xí)的興趣，為新課講授做好鋪墊。學(xué)生預(yù)習(xí)教材到位了，預(yù)習(xí)中產(chǎn)生的困惑就可以在課堂中得到很好的解決。教師布置預(yù)習(xí)作業(yè)也是備課中“預(yù)設(shè)”的重要環(huán)節(jié)，精心準(zhǔn)備的“預(yù)設(shè)”為的就是在課堂中精彩無限的“生成”。

蘇科版《矩形、菱形、正方形》第1課時(shí)預(yù)習(xí)作業(yè)布置：

作業(yè)一：利用所發(fā)材料，以小組為單位，制作門禁桿模型。

作業(yè)二：預(yù)習(xí)蘇科版八下教材P74-P75頁，以小組為單位，類比平行四邊形，歸納矩形的定義，發(fā)現(xiàn)矩形的性質(zhì)，完成學(xué)案第一部分“引導(dǎo)先學(xué)，自主探究”。

設(shè)計(jì)意圖：數(shù)學(xué)源自生活，生活離不開數(shù)學(xué)。課前讓學(xué)生參與模型制作的過程，感受生活中的矩形，從而激發(fā)學(xué)生學(xué)習(xí)的興趣，提高學(xué)習(xí)求知的欲望，知道數(shù)學(xué)的有用性。學(xué)生通過預(yù)習(xí)教材，能大體了解矩形的性質(zhì)，為課堂講解矩形性質(zhì)的證明做鋪墊。

二、鞏固所學(xué)，作業(yè)設(shè)計(jì)與課堂例題相吻合，突出作業(yè)布置的鞏固性

課堂作業(yè)是課堂效果的重要反饋。雙減下作業(yè)的布置更需要與課堂所授內(nèi)容相吻合，才能突出作業(yè)的鞏固性，同時(shí)減輕學(xué)生的作業(yè)負(fù)擔(dān)。

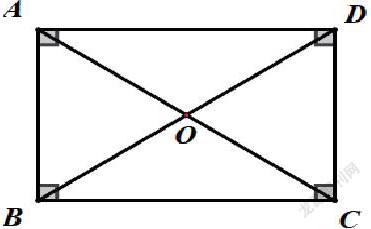
課堂例題：已知：如圖，矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O，且AC=2AB.求證：△AOB是等邊三角形.

課堂作業(yè)：

（1）改變例題中的條件AC=2AB為AD=AB.求證：△AOB是等邊三角形.

（2）請(qǐng)修改例題中AC=2AB這個(gè)條件，增加一個(gè)邊或者角的條件，以同桌為單位，一人出題一人求解，然后再交換。完成后展示出題解題的過程。

設(shè)計(jì)意圖：課堂例題講解中復(fù)習(xí)了等邊三角形的證明方法，并且規(guī)范了幾何書寫的證明過程。作業(yè)布置中仍然證明等邊三角形，再次鞏固證明方法，強(qiáng)調(diào)證明書寫的規(guī)范性。同時(shí)，第1題的設(shè)計(jì)復(fù)習(xí)了勾股定理，勾股定理的使用在與矩形有關(guān)的證明和計(jì)算題中非常重要。第2題采用同桌互助的方式交流展示，在學(xué)生自主命題和解題中體現(xiàn)新課標(biāo)的理念，突出學(xué)生在課堂中的主體地位，加深學(xué)生對(duì)等邊三角形證明方法的理解，復(fù)習(xí)特殊直角三角形的相關(guān)性質(zhì)及其應(yīng)用。

三、因需布置，作業(yè)設(shè)計(jì)與學(xué)生能力相匹配，突出作業(yè)設(shè)計(jì)的層次性

新課標(biāo)指出，初中數(shù)學(xué)需要讓每個(gè)人都能獲得良好的數(shù)學(xué)教育，不同的人在數(shù)學(xué)上獲得不同的發(fā)展[2]。學(xué)生在知識(shí)儲(chǔ)備、認(rèn)知水平、理解能力方面存在差異，因此作業(yè)的布置需要根據(jù)學(xué)生的特點(diǎn)因需布置，讓后進(jìn)生“吃的進(jìn)”，中等生“吃的飽”，優(yōu)秀生“吃的好”。

課后作業(yè)布置：

已知：如圖，矩形ABCD的對(duì)角線AC、BD相交于點(diǎn)O，若∠DBC=30°，DC=2.

基礎(chǔ)題：①求證：△COD為等邊三角形.②求矩形ABCD的面積.

拔高題：①若OD=CD=3，求∠DBC的度數(shù).②已知矩形面積為9，AB=OB，求CD的長度.

（3）拓展題：已知矩形面積為16，AB=OB，求點(diǎn)A到線段BD的長度.（請(qǐng)嘗試用不同方法求解，做好上課交流展示的準(zhǔn)備）

設(shè)計(jì)意圖：課后作業(yè)采取分層設(shè)計(jì)的策略。第1問是基礎(chǔ)題，要求全班同學(xué)均需完成并且掌握，證明等邊三角形再次鞏固了課堂所學(xué)內(nèi)容，并增加矩形面積的計(jì)算，復(fù)習(xí)面積的計(jì)算方法以及二次根式的乘法運(yùn)算。第2問適當(dāng)增加難度，考察的知識(shí)點(diǎn)更多，不僅需要證明等邊三角形，還需要利用等腰三角形性質(zhì)及三角形外角定理進(jìn)行角度的計(jì)算。已知面積反過來求長度可以采用方程思想，需要注意方程的負(fù)解要舍去。第3問更加綜合，求點(diǎn)到線段的長度需先作出垂線段，鼓勵(lì)學(xué)生用不同的方法求解，并在講評(píng)的時(shí)候給學(xué)生交流展示的機(jī)會(huì)。學(xué)生準(zhǔn)備時(shí)可以通過觀察出特殊幾何圖形直接求線段長度，也可以采用等面積法求線段長度。學(xué)生會(huì)做題不一定會(huì)講題，能把題講好的學(xué)生對(duì)題中所考知識(shí)點(diǎn)的理解會(huì)更深刻，對(duì)題型的掌握會(huì)更牢固，能全面提升數(shù)學(xué)素養(yǎng)。班級(jí)中會(huì)講題的學(xué)生多了，可以讓優(yōu)秀生去教后進(jìn)生，適當(dāng)減少優(yōu)秀生筆頭作業(yè)，學(xué)生作業(yè)負(fù)擔(dān)減輕的同時(shí)能力得到了提高，班級(jí)中學(xué)習(xí)的氛圍也會(huì)越來越好。

四、切合考試，作業(yè)設(shè)計(jì)與考試重點(diǎn)相結(jié)合，突出作業(yè)布置的高效性

評(píng)價(jià)學(xué)生知識(shí)掌握程度最客觀的方式就是考試。在中考?jí)毫χ拢處熑绻軌驅(qū)⒅锌伎键c(diǎn)滲透進(jìn)平時(shí)作業(yè)中去，對(duì)于減輕學(xué)生的作業(yè)負(fù)擔(dān)就大有裨益。此外，作業(yè)能否與考試重難點(diǎn)切合，提高學(xué)生學(xué)習(xí)的效率，是值得每一位老師思考的。數(shù)學(xué)教師布置作業(yè)前更應(yīng)該陷入“題海”，才能讓學(xué)生遠(yuǎn)離“題海”，在提高作業(yè)信度和效度的同時(shí)減輕學(xué)生作業(yè)負(fù)擔(dān)。

課后作業(yè)鏈接中考：

設(shè)計(jì)意圖：課后作業(yè)增加中考鏈接這個(gè)環(huán)節(jié)，讓學(xué)生看一看最近一年中考中本節(jié)課所講內(nèi)容是如何考查的，了解考試的方向，再次明確本節(jié)課所需要掌握的內(nèi)容。第1題計(jì)算線段長度，考查矩形對(duì)角線互相平分且相等的性質(zhì)。第2題考查特殊矩形中存在的底角是30°的等腰三角形與含30°的直角三角形，讓學(xué)生體會(huì)一般與特殊的關(guān)系。第3題利用矩形四個(gè)角是直角和對(duì)邊相等的性質(zhì)，復(fù)習(xí)了三角形全等以及平行四邊形的判定。

作業(yè)的設(shè)計(jì)需要基于學(xué)情，以中考為方向，發(fā)揮預(yù)習(xí)作業(yè)的前瞻性，課堂作業(yè)的鞏固性以及課后作業(yè)的層次性，教師精心設(shè)計(jì)適合自己學(xué)生的作業(yè)，努力讓“減輕義務(wù)教育階段學(xué)生作業(yè)負(fù)擔(dān)”真正落地。

參考文獻(xiàn)

[1]潘虹.基于學(xué)生發(fā)展核心素養(yǎng)的初中數(shù)學(xué)作業(yè)設(shè)計(jì)[J].教學(xué)與管理，2017（8）：45-46.

[2]義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[M].北京：北京師范大學(xué)出版社，2012.