大概念導向下的單元學習任務設計路徑

【摘? ?要】以大概念為導向的單元教學是當前國際教學發展的新趨勢，為小學數學課程落實學科核心素養帶來新的契機和可能。在確立單元大概念之后，教學應以單元大概念為導向，以預期結果為航標，規劃設計具體的學習任務，從而實現真實的深度學習。具體實踐路徑有三：以“大概念”邏輯重組“學習內容”;用“預期結果”統領“學時目標”;從“基本問題”演化“學習問題”。

【關鍵詞】大概念;學習任務;設計策略

單元整體教學已成為當下教學研究的一大熱點，并出現了用大概念、大項目和大問題等方式組織單元教學的具體實踐，以切實解決學習缺乏整體性、知識之間缺乏關聯性等教學問題。其中，由格蘭特·威金斯（Grant Wiggins）和杰伊·麥克泰格（Jay McTighe）提出的，旨在促進理解與遷移的“大概念”導向的單元教學設計備受關注。

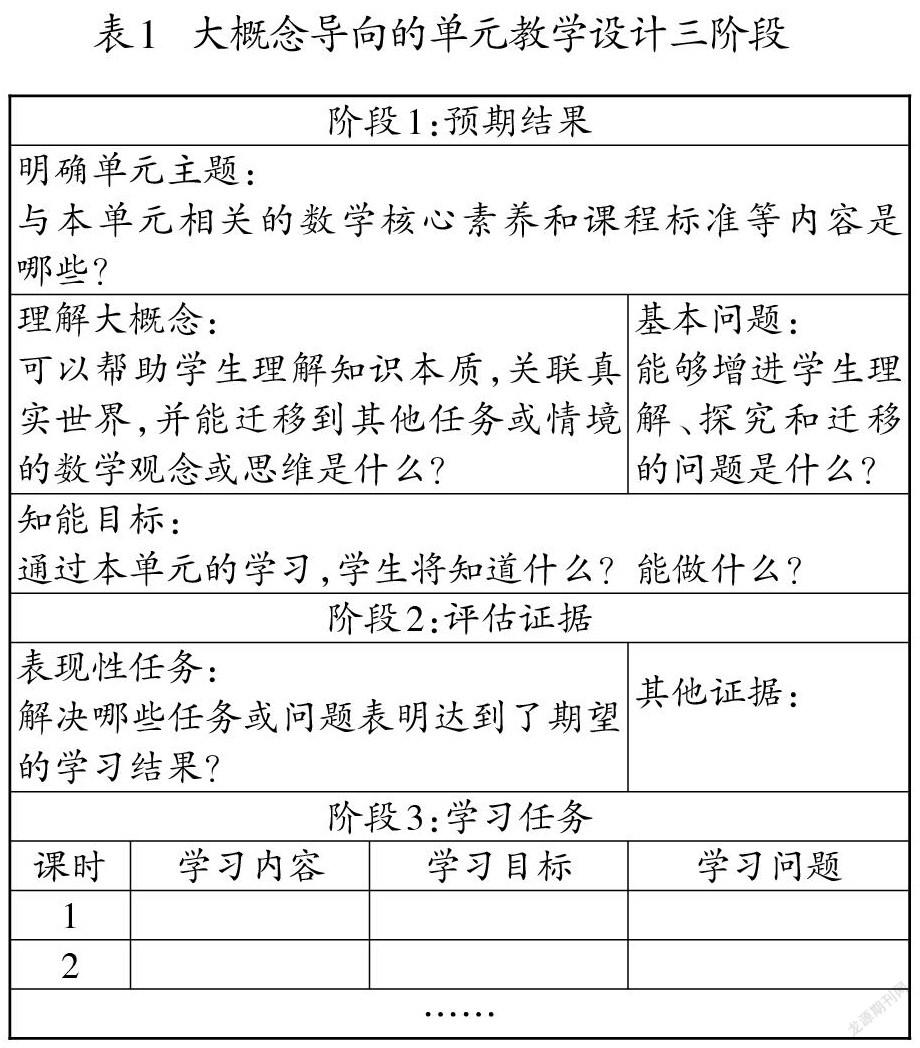
大概念導向的單元教學強調以終為始，進行教學設計時主要經歷三個階段（如表1）：首先是明確預期結果，含明確單元主題或標準內容，理解大概念、基本問題和確定知能目標。其次是確定恰當的評估證據，包括表現性任務和其他證據。最后是規劃相關學習任務，含課時進度、學習內容、學習目標和引領課堂教學的學習問題等。在完成單元大概念提取、基本問題提煉、單元知能目標確定等工作之后，學習任務這個操作重點，即階段3中的學習內容、學習目標和學習問題又應該如何規劃和設計呢？怎樣的操作路徑，能較好地讓具體的學習任務與預期的結果保持一致，從而實現單元整體教學和大概念導向呢？

一、以“大概念邏輯”重組“學習內容”

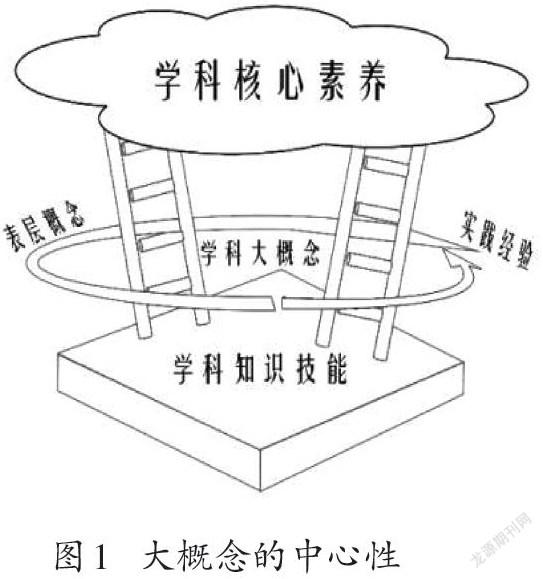
大概念將課程知識與數學核心素養兩個不同的范疇聯結起來，是促進學科知識技能向核心素養轉化的中介機制。大概念將外部活動經驗向內轉化為認知結構，又將內部認知結構向外轉化為具有現實力量的核心素養。這種獨特的結構性決定了大概念對于學生的學習具有指導作用，它能夠“向下”整合知識與技能，“向上”聯通核心素養，“向外”整合表層概念和實踐經驗（如圖1）。因此，它與以往單元教學最大的不同在于，學習任務要緊緊圍繞單元大概念的邏輯設計，而非簡單地按教材內容組織，并需考慮大概念之間、小概念與大概念之間的關聯。據此劃分課時內容，選取相應的素材和資源。

如人教版教材“圖形的運動”的學習內容中包括了軸對稱圖形、平移和旋轉等知識點，這些內容分別安排在四年級下冊和五年級下冊。其大概念為“在動態變化過程中，存在不變的元素和運動變化的規律（也是人類探索數學知識和未知世界的基本方法）”。以大概念邏輯重組后，教師可以對學習內容進行如下規劃。

第1課時，安排相對直觀的“平移”教學任務，通過“什么變了？什么沒變？為什么變或不變”等問題，形成平移后圖形沒有發生變化，是因為“平移是圖形上所有的點按照同一方向移動同樣的距離”的概念，并初步建立“理解變化，要去探究變化的規律和不變的要素”的大概念。第2課時，安排學習“旋轉”，建立“旋轉是圖形上所有的點，以一個點為中心，按照同一方向移動同樣的角度”的概念，完善建立單元大概念。第3課時，帶著頭腦中已有的“大概念”，學習“軸對稱”，發現軸對稱圖形是圖形上所有的點，以一條線為軸，翻轉后形成的圖形。第4課時，安排一個綜合性的問題解決案例，幫助學生進一步理解三種圖形運動之間的聯系及區別，形成完整的知識結構。

又如在杭州市特級教師袁曉萍設計的《圓》的學習任務中，同樣緊緊圍繞“借用直方圖形有利于理解圓的特征”這個大概念進行學習內容的重組，整合設計了“圓問”“找圓心”“尺規作圖”“圓周率與割圓術”“周長與面積”“生活中的圓”“環形運動軌跡”“神奇[π]/4”“方圓之間”等學習任務。

可以說，圍繞大概念邏輯組織學習內容和資源，就像“滾雪球”一樣具有累積效應，不僅可以打通不同內容之間的邏輯關系，幫助學生織成具有規律的結構之網，還能幫助學生融通跨學科的知識和真實世界。

二、用“預期結果”統領“課時目標”

大概念導向下的單元教學設計的“預期結果”中，“明確主題”體現了學科課程標準和學科核心素養的基本要求，“大概念”體現了綜合性的高階目標，指向真實世界的問題解決，“知能目標”則是本單元所應掌握的知識和技能。在課時目標確定時，要先把預期結果作為“統領”，并與其保持一致，然后結合學習內容將其具體化為預期可見的每個課時的學習目標。

以人教版三年級下冊“兩位數乘兩位數”一課為例。本單元的大概念是“兩位數乘一位數的方法可以推及到其他多位數乘法運算”。“兩位數乘兩位數”的學習起點是“多位數乘一位數”，乘法豎式的樣子從以前的“一層”跨入了“兩層”。同時，它又是通過推理獲得“多位數乘兩位數”的算理。依據這些信息以及知識與概念之間的關系，就能較好地確定本課時的學習目標（如圖2）。

因此，“兩位數乘兩位數”一課的具體目標為：掌握兩位數乘兩位數（不進位）的筆算方法，并能正確計算。通過探究、討論，理解算理和多位數乘法的基本結構。結合算理探究與算法歸納的過程，建立“兩位數乘一位數的方法可以推及到其他多位數乘法運算”的大概念。

三、從“基本問題”演化“學習問題”

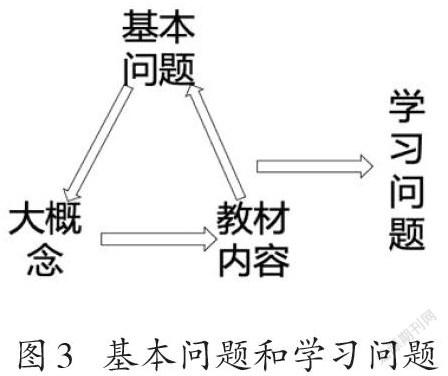
在單元設計中，基本問題和大概念是相配套的，是大概念活化后的高質量問題。威金斯等將基本問題比作大概念的航標，認為最好的問題是指向和突出大概念的，通過它們，學習者可以探索內容中或許仍未被理解的關鍵概念、主題、理論、問題，在借助啟發性問題主動探索內容的過程中加深對概念的理解。因此，每一課時學習的主要問題要指向基本問題，并結合教材內容和課時目標，觀照大概念演化出學習問題（如圖3），這樣可以幫助學生引發與大概念相關的持續性思考，不斷激活具體經驗，達成深度理解。

如在人教版五年級下冊“分數加減法”單元中，有同分母分數加減法、異分母分數加減法、混合分數加減法三個主要學習任務，其單元大概念是“單位相同的數才可以直接運算”。為了更好地理解分數運算的算理，就應該從“兩個分數可以直接加減嗎，為什么”的基本問題出發，分別演化出“為什么分子（同分母）可以直接相加減”“為什么分子（異分母）不能直接相加減”“什么情況下三個或多個分數能直接相加減”等學習問題，引領學生思考和討論。

相反，如果教師直接問“怎么相加？怎么做就能相加”，試圖引導學生回答事先已有的固定結論或答案，就會遠離與大概念相配套的“基本問題”，相應的教學也不可能建立起 “大概念”，而是回到了傳統教學中的技能、技巧的掌握。

又如在人教版二年級下冊“萬以內數的認識”單元中，單元大概念是“十進計數方法是遇九拐彎、滿十進一”，基本問題則是“新數怎么寫？表示什么意思”。在引導學生認識“萬”時，通過“數9585到9590、9590到9600、9600到10000”這個過程，利用演化而成的學習問題“下一個數是什么？你是怎樣想的”，激發學生用“遇九拐彎、滿十進一”的結構去建構更大的數和計數方法，從而實現“知其然，知其所以然”。

學習任務中的問題設計從基本問題演化開始，就能緊緊圍繞大概念這個中心，從而讓學生有更大的可能受到自身學習經驗和生活價值的引導，激活豐富生動的真實世界，進入到有意義的學習狀態。

上述的大概念導向下的單元學習任務的設計路徑，是組織落實單元整體教學的具體方法，但在后續實施中肯定還會遇到很多困難。首先，目前的具體實踐還是局限在部分教學內容中，需要持續進行思考和實踐，包括更多的學習領域、更具體的路徑、更豐富的呈現方式等問題，要避免形式化、隨意化。其次，學習任務設計是系統工程，涉及諸多問題，本文提及的實踐路徑尚未將最難的第二階段中的“評估證據”納入整體思考，這也將是課題組下一步思考和探索的重點。第三，面對這些棘手的問題，教師要加強理論學習，深化學習任務背后的理論基礎。同時，課題組在教學實踐中要充分發揮專業共同體的力量，一起合作開發，打通大概念導向的單元整體教學的“最后一公里”。

參考文獻：

[1]威金斯，麥克泰格.追求理解的教學設計：第二版[M].閆寒冰，宋雪蓮，賴平，譯.上海：華東師范大學出版社，2017.

[2]李松林.以大概念為核心的整合性教學[J].課程·教材·教法，2020（10）.

[3]劉徽.“大概念”視角下的單元整體教學構型：兼論素養導向的課堂變革[J].教育研究，2020（6）.

[4]邵朝友，崔允漷.指向核心素養的教學方案設計：大觀念的視角[J].全球教育展望，2017（6）.

[5]胡曉敏.單元“大概念”的提取策略[J].教學月刊·小學版（數學），2020（12）.

[6]章勤瓊，陳錫成.基于學習路徑分析的小學數學單元整體教學思考框架[J].小學教學（數學），2021（3）.

（浙江省杭州市創意城小學? ?310051）