核心素養視域下立體幾何定理教學研究

沈宏

[摘 ?要] 高中立體幾何定理教學是發展學生直觀想象、邏輯推理核心素養的重要載體. 文章以高中“平面與平面垂直的判定”教學為例，探討核心素養視域下高中立體幾何定理的教學策略.

[關鍵詞] 核心素養;立體幾何;定理教學

高中立體幾何教學的價值在于訓練學生的空間想象思維，不斷完善學生的公理化思想，有效培養學生的分析運算、邏輯論證等能力. 而定理教學又是立體幾何教學的“重中之重”，是發展學生直觀想象、邏輯推理核心素養的重要載體[1]. 因此，在高中立體幾何定理教學中，教師應確立核心素養培育指向，引領學生深入探究其蘊含的數學思想方法和知識技能，充分運用數學的思維方式認識和分析世界，成為高中立體幾何定理教學的關鍵.

高中立體幾何定理教學內容分析

對于高中立體幾何的知識與技能而言，相當數量的教師往往采用操作確認、直觀感知、度量計算的方式研究世界物體的大小、形狀和位置關系，結合李藝、鐘柏昌等學者對核心素養的研究以及對其內涵和結構的分析，其中以基礎知識和基本技能為核心的最底層——“雙基層”就是應用立體幾何定理證明一些空間位置關系的命題;以解決問題而獲得基本方法為核心的中間層——“問題解決層”就是通過立體幾何的觀察與實驗、概括與抽象、模型與構造等獲得解決問題的基本思路和方法;而以思考問題、解決問題的思維方法和價值觀為核心的最高層——“學科思維層”就是在立體幾何定理的探究中，樹立和培養應用有限、研究無限，由少到多、層層深入研究的數學基本觀念. 也就是說，在高中立體幾何定理教學中均是以“探究”為關鍵，要求學生不斷體會定理的抽象過程，發展空間想象思維，逐漸提升學生的分析運算、邏輯論證等能力.

同時，立體幾何定理教學還應體現在高中數學思維之中，其中，在判定定理教學中，由于判定定理的證明目標十分明確，因此教師僅需要引導學生通過添加直線這一新元素，就能將抽象的立體幾何問題轉化為可以應用兩相交直線確定平面的熟悉命題，從而幫助學生完成相關定理的探究. 而在性質定理教學中，由于性質定理的證明目標不明確，往往會出現很多線面關系的性質，因此教師可能需要引導學生添加不止一個關于線、面的新元素獲得新命題. 實質上，高中立體幾何八大定理的教學有效貫徹了數學的學科思維，在一定程度上很好地體現了學生數學核心素養培養的要求和目標.

核心素養視域下高中立體幾何定理教學實踐

下面以高中“平面與平面垂直的性質”教學為例，探討核心素養視域下高中立體幾何定理的教學策略.

1. 強化復習

為了體現由本源發展一系列知識的數學學科方法，體會元素由少到多、由簡單到復雜的過程，不斷強化學生的“學科思維層”，教師應及時組織學生復習直線與平面垂直的內容，利用知識遷移不斷反復強化和刺激知識的形成過程，有效為新定理的探究做好鋪墊.

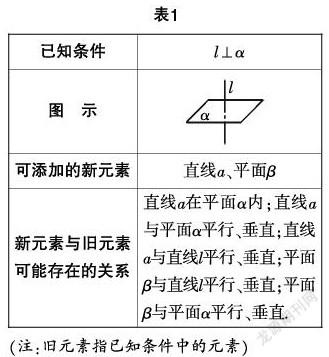
例如，為了強化幾何定理的研究方法，教師可以設計類似表1的表格形式組織學生復習直線與平面垂直性質的探究過程.

2. 探究發現

探究是培養學生“學科思維層”的最好實踐，是學生內化知識、解決問題的過程. 因此，為了開啟學生的創新思維，教師可以用“日常生活中如何判斷兩平面相互垂直，以及兩平面垂直時所具有的性質”為主題，要求學生充分明確課堂教學所研究的對象. 值得說明的是，由于“平面與平面垂直的判定”并不是第一次開展立體幾何定理探究，因此，為了進一步溫故和遷移所學知識，教師可以采用競賽的方式組織學生發現新性質.

例如，為了發展學生的抽象思維，促使學生在發現新性質的過程中找到思維漏洞，直觀感受過程中的“創新”，發現新性質的過程可以通過表2所示的整理性質的方式實施.

3. 定理證明

為了體現核心素養的“雙基層”內涵，不斷明確性質定理的概念，教師應及時對上述探究所獲得的性質進行甄選，要求學生深刻反思表2所示的①、②、③、④、⑤、⑥等過程探究中哪一個或者幾個應用到了平面與平面垂直的性質定理，并引導學生明確除表2中的①和⑥未運用到面面垂直的條件外，其余四個過程探究均應用到了面面垂直的條件;并且按照性質定理簡潔、有用的選擇標準，過程探究②最適宜作為平面與平面垂直的性質定理，即平面α與平面β相互垂直，若其中一個平面內的直線垂直于這兩個平面的交線，則這條直線也垂直于另一個平面[2].

隨后，要求學生應用數學符號抽象該性質，即已知α⊥β，α∩β=a，若b⊥a，b？奐β，則b⊥α. 為了體現核心素養的“問題解決指向”內涵，教師還應要求學生通過小組合作方式研討獲得平面與平面垂直的性質定理的基本思路，不斷提升學生的學習技能.

4. 課堂總結

課堂總結往往要求學生總結出相應的思想方法和知識目標，有效將所學知識建構到自己的知識結構中. 在這一過程中，除了要總結平面與平面垂直的性質定理以及相應的證明方法外，還應總結添加新元素的研究方法，以及思辨論證等立體幾何數學觀;在此基礎上還應設計以提高學生數學語言表達能力為主的“數學思維層”方面的作業，以及以提高和發展學生技能為主的“雙基層”方面的作業.

核心素養視域下高中立體幾何定理教學思考

（1）由于每個教學內容所涉及的數學核心素養各不相同，因此，在確定教學目標時務必將知識發生發展的過程作為教學重點，不斷引導學生體會和總結知識發生發展的過程. 以確定立體幾何定理教學目標為例，其所涉及的核心素養主要為直觀想象、邏輯推理以及數學抽象，因此教師可以將其設計為雙基層、問題解決層、數學思維層三個方面[3]. 值得一提的是，依靠短時間的實踐很難產生深遠的學習影響，因此需要教師持之以恒，在知識探究螺旋上升的過程中逐漸深化數學思維和數學觀念.

（2）現有課堂除了概念、公式的教學外，還常常設置了課堂練習，而為了更加突出學生的體驗和發現，教師還應勇于突破教材設計和教學模式的限制，最大限度地給予學生充分的探究機遇和探究時間. 值得注意的是，這并不是說教材中的例題和課堂練習不重要，而是可以通過專門的習題教學達到上述教學的目的. 同時，過度細分教學內容往往會使教學目標過于明確，這在一定程度上限制了學生思維的創新和發展，不利于學生的深度學習探究.

結語

總之，核心素養視域下的高中立體幾何定理教學，教師應自覺投入課堂教學實踐，促使學生主動探究，從而獲得相對穩定的思考和解決問題的價值觀和思維方式，只有這樣，才能更好地理解和實踐數學教學，才能獲得認識和改造世界的觀念和方法.

參考文獻：

[1] ?朱致航. 單元教學視角下立體幾何定理教學[J].中學數學（高中版），2021（07）：84-85.

[2] ?丁益民. 例談立體幾何概念（定理）教學中的邏輯建構[J]. 數學通訊，2017（06）：32-33，45.

[3] ?徐琴. 高中數學立體幾何教學的幾點思考——以“平面與平面平行的判定定理”為例[J]. 數學教學通訊，2017（18）：58-59.