基于學生數學素養發展的創新試題設計

錢春燕

［摘? 要］ 適切地設計和改編創新試題不僅可以體現學科的寬度，還對培育創新意識和數學素養具有一定的導向作用。文章基于學生數學素養，針對封閉性數學試題進行改進，提出聚焦學生數學素養發展的創新試題改編路徑：探究性創新試題——積累思維過程的智慧點；導向性創新試題——提升思維的參與度；過程性創新試題——孕育邏輯推理；層次性創新試題——強化綜合應用能力。

［關鍵詞］ 創新試題；數學素養；小學數學

數學教學不僅要關注知識技能，還應著眼于學生創新思維的培養。那么，如何開啟學生的創造潛能，如何培養學生的創新意識，就成了教學改革的重要目標。小學階段是學生創造性培育的初始階段，創新試題具有挑戰性，可以極大地激起小學生的好奇心。因此，適切地設計和改編創新試題不僅可以體現學科的寬度，還對培育創新意識和數學素養具有一定的導向作用［1］。如何設計創新試題？筆者依據教學內容和學生學情進行了一些有益的探索，與各位同行分享。

[?] 一、探究性創新試題——積累思維過程的智慧點

探究性問題可以激起學生認知心理上的沖突，讓學生產生探究的心理狀態，以尋求解題的各種方法策略，從而積累思維過程的智慧點。因此，教師應改習題為問題，努力設計好具有探究性的創新問題，試圖開發學生思維潛能，幫助學生積累數學“原始”發現的經驗，提高學生的探究能力和思維水平［2］。

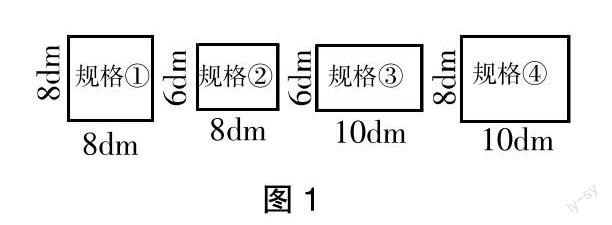
例1? 圖1是幾種不同規格的鐵皮（有長方形和正方形兩種）。

（1）利用6張規格①的鐵皮，可以焊接出一個__________體油箱，該油箱的表面積是_____________，容積是__________。（焊接處忽略不計）

（2）若再利用規格②③④各兩張去焊接一個長方體油箱，則該油箱的表面積是_________，容積是_________。（焊接處忽略不計）

原題分析：本題的兩個小題都考查如何求立體圖形的表面積和體積，此設計顯然層次性不明顯，不具有探究性。因此，筆者對第（2）問進行了改造，將一個同一層次的“習題”轉化為具有一定開放度和創造性的“問題”，讓學生在探究和解決問題的過程中經歷思維的流暢和發散訓練。

改編后的第（2）問：倘若還需要焊接一個長方體的油箱，該如何選擇鐵皮？（請畫出展開示意圖，并寫清楚選擇的鐵皮規格及張數）

方案1：______________________

方案2：______________________

方案3：______________________

點評：筆者在改造中將問題打開，給予學生更多的思考和想象的空間，鼓勵學生大膽運用直覺和想象去猜測，運用各種途徑去尋求任意可能的方案。在這個過程中，學生自然也能開動腦筋，還問題更多的驚喜，提出了許多巧妙的方案，使得本題的探究價值得到了進一步提升。

[?] 二、導向性創新試題——提升思維的參與度

一般情況下，試題過易，學生會深感索然無味；試題過難，學生又會產生畏難心理。基于此，教師在設計試題時，需要充分把握好問題的難易程度，對于一些難度過大的試題，可以將探究問題作為導向性指引，這樣一來，才能給予學生思路上的指引，以提高學生思維的參與度。

例2? 如圖2，小正方形的面積是10cm2，則圓的面積是_________。

原題分析：學生在解決本題時習慣性地去探求圓的半徑，那么自然由于無法探求而思維受阻，此時，則易產生畏難情緒。為了讓學生的思維更加順暢，筆者對本題進行了以下改編。

（1）如圖2，小正方形的面積是10平方厘米，即________。

（2）根據圓面積計算公式，若π≈3，據上述關系可求出圓的面積：S=_____。

（3）圖2中的大正方形面積是___，根據這樣的圖形關系，若要在一張面積是60平方厘米的正方形紙上畫出一個最大的圓，那么這個圓的面積是_____。（π≈3）

點評：為充分延展學生的思維，最大化地利用好本題的圖像特色，筆者有意識地將本題進行了改造，改編后的問題更利于學生觀察和思考，使學生通過探尋圖形間的聯系來完成問題的解析，促進創新思維的發展。

[?] 三、過程性創新試題——孕育邏輯推理

問題孕育創新，問題是創新之“始”，也是創新之“母”，教師在設計創新試題時不僅需要關注問題的導向性，還需關注過程性。因為，解決一道數學問題并非僅僅考查學生的解題思路與策略，在很大程度上也是對推理能力的考量。倘若教師在改編一些較為抽象難懂的試題時可以注意到過程的細化，則可引發學生的猜想，讓學生進一步有序思考和分析問題，以實現對邏輯推理和分析能力的培育。

例3? 紅紅和芳芳正在玩卡片游戲，每個人從2，4，5，7這4張卡片中任抽一張，若兩數之積為偶數，則紅紅贏，反之芳芳贏。依照這樣的玩法，則（? ? ）。

A. 芳芳贏的機會大

B. 紅紅贏的機會大

C. 兩人贏的機會相同

原題分析：本例最顯著的特點是抽象性大，大部分學生是直接判斷贏的對象，那么思考過程就直接省略了，無法考查學生的思考過程。倘若這里能通過細化問題，讓過程顯性化，則可以達到訓練邏輯推理能力的效果。為此，筆者進行了如下改編。

紅紅和芳芳正在玩卡片游戲，每個人從2，4，5，7這4張卡片中任抽一張，若兩數之積為偶數，則紅紅贏，反之芳芳贏。

（1）隨意抽出的卡片中，兩個數的積有可能出現以下結果：2×4=8，______________________。（請寫出可能出現的所有結果）

（2）按照這樣的玩法，芳芳贏的可能性可以用分數______表示。

（3）按照這樣的玩法，則（? ? ?）。

A. 芳芳贏的機會大

B. 紅紅贏的機會大

C. 兩人贏的機會相同

（4）在不改變游戲規則的情形下，將4張卡片中的數字_____換成____，這個游戲就公平了。

點評：問題在教師的改編下，有了有序思考的靈魂，有了透徹理解“可能性”和“游戲公平”的支柱，最重要的是改造后的問題開放性較強。此時，由于習題是開放的，學生的求解思路是延展的，有利于發散性思維的培養。

[?] 四、層次性創新試題——強化綜合應用能力

每個學生都是獨特的個體，尤其在知識、能力等因素上有很大的差異。傳統試題不僅“題海無邊”，更是形式單一，常常讓一些學生在遇到稍有難度的試題時思維卡殼。事實上，人的經驗反饋網絡具有一定的層次性，作為一定經驗基礎上的習題設計也應具有相稱的層次性。因此，教師應富有創造性地改編問題，讓改編問題具有層次性和創造性，這樣才能在深化知識理解的同時增強學生的綜合應用能力。

例4? 一輛巴士從A城開往B城，已經行駛了全程的3/10，此時距離B城還有84千米，試求出A城和B城的距離。

原題分析：顯然，面對這樣一道復雜的行程問題，一眼看不到解題的具體思路。而以解決問題為線索進行問題的改造，探尋深入追問的機會，則可以有效拓展學生的思維空間，讓解題思路流暢而自然地顯露出來。于是，筆者對原題進行了如下改編。

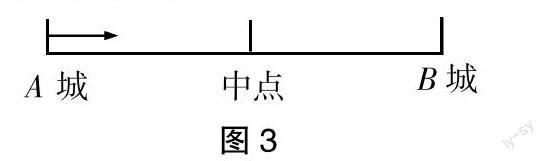
一輛巴士從A城開往B城，行駛了全程的3/10。

（1）試著在圖3中用▲標注此時巴士行駛的位置：

（2）若此時巴士距離B城的距離是84千米，試求出A城和B城的距離。

（3）若此時巴士距離A、B兩城的中點還有20千米，試求出A城和B城的距離。

（4）一直以這樣的速度行駛下去，該巴士到達B城還需要多長時間？

（5）巴士的油箱原有78升汽油，此時剩下了54升，按照這樣來算，剩余的汽油量能行駛至B城嗎？

點評：所有的“教”都是為了“學”，改編問題的最終目標是讓學生“學好”，故而要明確問題設計的“價值”追求，簡而言之就是改編問題的目的所在。試題經筆者之手改編后由“知識立意”轉變為“能力立意”，充分體現了“能力立意”的思想。事實上，這樣的改編一方面降低了試題的難度，如第（1）（2）問雖為基礎題，但指引學生借助數形結合進行思考也是其本質目的。之后的3個問題的難度逐步加深，并滲透了幾分挑戰性，讓學有余力的學生可以充分體驗探究和收獲的喜悅，這種走向層次性的創新試題改編取向本身也是向學生傳播創造性思維［3］。

總之，新課程理念下推崇創新意識和創造潛能，是值得教師傾聽和思考的。教師唯有用發現的眼光進行試題設計，才能拓展學生的思維，讓更多的學生愛思考、愛探究、愛學習，發展數學素養。想來，這種走向素養提升的創新試題改編也是值得教師繼續努力的。

參考文獻：

［1］? 邱貞輝. 初中數學例題及習題教學設計研究［J］. 中學課程資源，2017（01）：26-27+34.

［2］? 左俊鳳. 充分利用教材培養學生的探究意識［J］. 中學數學，2003（02）：13.

［3］? 雷淇未. 利用教材例題培養學生創造性思維［J］.中學數學月刊，1997（11）：10-11.