指向數據分析能力培養的教學實踐與探索
王璨

[摘? 要] 以“復式折線統計圖”為例,嘗試進行指向數據分析能力培養的教學實踐與探索,以培養學生數據分析能力為核心,使學生意識到利用統計的方式解決問題的獨特優勢,并引導學生通過對數據的對比和分析,預測數據的未來發展趨勢,從而把學生的數據分析能力提升到一個新的層次。
[關鍵詞] 數據分析;教學實踐;教學探索;復式拆線統計圖
伴隨著科學信息的快速發展,人類社會逐漸進入“大數據”時代,人們越來越多地面臨煩冗復雜的數據信息,如何從這些海量的數據信息中發現數據本身的規律,提取對自身有用的信息呢?培養學生的數據分析核心素養就顯得至關重要。因此,在小學數學的教學中,教師要引導學生在解決問題的過程中,通過收集數據、整理數據、分析數據和描述數據等環節,揭示某一事物的發展規律和未來趨勢,并在此過程中,培養學生的數據分析能力。筆者以“復式折線統計圖”為例,嘗試進行指向數據分析能力培養的教學實踐與探索,期望為廣大教育同人提供有價值的借鑒和思考。
[?]一、創設情境,引出復式圖
“好的開端是成功的一半。”在新授課中,教師不必急于切入主題,可結合小學生身心發展特點和認知規律,創設生動的情境,把學生的思維逐步導入新課的學習中。關于新課導入,教師可從以下兩個方面把握:一是從現實生活入手。小學生對知識的認知往往源于現實生活中的具體事物和實例,教師以現實生活中的事物切入主題,往往就能吸引學生的注意力。二是把握新知識與舊知識的聯系,引發思維沖突。數學新知識與舊知識之間往往存在著比較密切的聯系,教師可以從新舊知識連接點入手,使學生運用舊知識解決問題時產生困惑和迷茫,使之處于“思之而不得”的心境中,由此產生對學習新知識的強烈渴望。
師:同學們,現在大家已經上六年級了,你們的身高各是多少呢?
生1:我的身高是150厘米。
生2:我的身高是153厘米。
生3:我的身高是154厘米。
師:從一年級到六年級,同學們的身高都發生了很大的改變。那么,你的身高與全市學生的平均身高相比,是更高些還是更低些呢?表1是小李同學收集到的數據表。
師:同學們觀察這些數據,說一說小李在幾年級的時候與全市男生平均身高的差距最大。
生4:我們需要先把小李身高與全市男生平均身高之差算出來,然后比較大小。具體為:一年級是118-115=3(厘米),二年級124-122=2(厘米),三年級是130-130=0(厘米),四年級是138-135=3(厘米),五年級是145-143=2(厘米),六年級是154-153=1(厘米)。所以,在一年級和四年級時小李身高與全市男生平均身高的差距最大。
生5:這個辦法計算起來比較麻煩,而且也不直觀。如果能把這些數據都畫在圖上再進行比較,就方便多了。
生6:我們已經學過折線圖的畫法。我可以把小李身高和全市男生平均身高分別畫在折線圖上,這樣就能比較了。
生5:這樣也不好。兩條折線不在同一個圖上,比較起來還是比較麻煩。
師:那我們能不能把兩條折線畫在同一個圖上形成一個復式統計圖呢?
(學生議論)
師:心動不如行動。我們還是動手嘗試一下吧!
教學中,教師引導學生運用前面學習的單式折線圖解決現實問題,結果學生發現僅憑單式折線圖并不能很好地比較小李身高與全市男生平均身高,這就引起了學生的思維沖突,使學生產生了學習新知識解決問題的欲望。
[?]二、整理數據,繪制統計圖
繪制統計圖是學生學好數學的一項重要能力,也是培養學生數據整理和數據分析能力的重要途徑。課堂教學中,教師要充分調動學生的積極性,引導學生親自動手繪制統計圖,把表格中的數據轉化到生動直觀的統計圖中,使學生初步體驗統計圖的直觀優勢。在這個過程中,需要注意的是,一要引導學生整理數據。正確地整理、分析數據是繪制統計圖的基礎。在繪制復式折線圖的過程中,對于縱軸的數據分段是提升學生整理、分析數據的關鍵環節。二要注重繪制細節。在繪制過程中,教師要引導學生把數據準確地體現在圖上,要求學生注意作圖的規范性,最大限度地減少繪制過程中的誤差,這樣不但能培養學生細致嚴謹的數學精神,還可以為下一步的數據比較和預測打下基礎。
師:在畫圖之前,我們先要明確,用橫軸代表什么項目,用縱軸代表什么項目?
生7:可以用橫軸代表年級,可以用縱軸代表身高。
師:那么,應該把身高分為幾段呢?
生7:最低的身高是115厘米,最高的身高是154厘米。所以可以把110厘米作為縱軸上除0以外的第一個數據;(154-110)÷5≈10(厘米),所以用1個大格代表10厘米,也就是把身高的數據分為5個段,分別是110—120、120—130、130—140、140—150、150—160(單位:厘米)。
師:確立了橫軸和縱軸代表的項目,又確定了縱軸上的單位長度,那么,還有一個問題需要解決,如何區分開兩條折線呢?
生7:可以用兩種不同顏色的線,這樣就能區分開了。
師:如果只有一種顏色的筆呢?
生8:那我們可以用實線和虛線分別代表不同的數據。
師:明確了這些問題,我們現在可以開始畫圖了。
(學生畫圖,教師巡回指導)
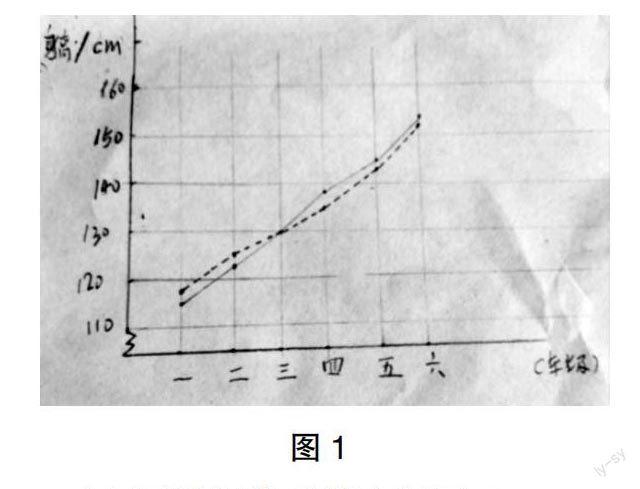
生7:這是我畫的圖(圖1)。我先確定縱軸上的單位長度,用1個大格(1厘米)代表10厘米,然后在統計圖上按照數據描出各個點,再分別用虛線和實線把各個點連接起來。
師:同學們能看懂這幅圖嗎?
生8:虛線代表什么,實線又代表什么呢?
生7:虛線代表全市男生的平均身高,實線代表小李的身高。
師:每個人看自己的圖,都能明白每條線代表誰的數據。可是,統計圖是用來交流的,在很多時候是給別人看的,我們怎么樣能讓別人一眼就看懂我們畫的圖呢?
生7:我們可以在圖上標出來每條線代表誰的數據。
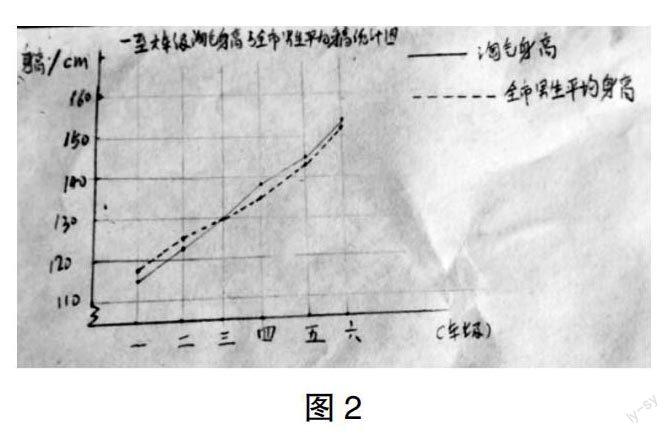
師:對,這就是圖例。圖例要寫在統計圖的右上角。
(生7在統計圖上加上圖例)
師:如果我把這幅加上圖例的統計圖拿給別人看,別人能看得懂嗎?
生9:別人可能會有這樣的疑問:這幅統計圖描述了什么事情?
師:所以,我們還要給這幅統計圖起個名字,在統計圖上方注上標題。
生7:這樣就比較完整了。
師:同學們,這就是復式折線統計圖。大家把它和以前我們學過的單式折線統計圖對比一下,看看它們有什么區別。
生7:單式折線統計圖有一條線,而復式折線統計圖有兩條線。
生8:單式折線統計圖只能直觀地看出一個事物的發展變化情況,而復式折線統計圖能夠看出兩個事物的發展變化情況。
生9:通過復式折線統計圖可以容易地比較兩組數據,并體現數據的變化趨勢。
教學中,繪制復式統計圖既是一個學生運用繪圖工具作圖的操作過程,同時也是一個學生整理數據、分析數據的過程。首先,教師引導學生通過觀察、計算數據,確定在縱軸上用1個大格代表10厘米,培養學生的數據整理和分析能力;其次,教師通過“加圖例”“寫標題”等環節,使學生繪制的復式折線統計圖逐漸完善,并在這個過程中培養學生嚴謹認真的治學精神;最后,通過對比單式折線統計圖和復式折線統計圖,既溝通了新舊知識的聯系,又使學生初步體驗了復式折線統計圖的優勢。
[?]三、多層次分析,解讀統計圖
數據分析能力是信息社會對公民提出的重要要求。數據分析能力是建立在學生數據搜集、數據整理、數據分析和數據描述的基礎上逐漸形成的。要提升學生的數據分析能力,最有效的辦法就是讓學生真正經歷數據分析的過程。學生從統計圖表中獲得信息,并依據這些信息進行分析、判斷,最后對事物未來的發展方向做出預測。教師要引導學生對數據做出多層次分析,逐漸激活學生的數據分析觀念,提升學生的數據分析能力。
師:從統計圖上看,小李身高在幾年級時與全市男生平均身高相差最大?在幾年級時二者相差最小?
生10:從圖上看,在一年級和四年級時,小李身高與全市男生平均身高的差距最大,在三年級時二者的差距最小。
師:你是怎樣看出來的?
生10:兩條折線之間的距離越大,說明兩組數據的差距越大;兩條折線之間的距離越小,說明兩組數據的差距越小。
生11:復式折線統計圖讓數據的比較變得更加直觀了,也更加簡單了。
師:小李身高在哪個階段增長得最快?
生12:小李身高在五年級到六年級這個階段增長得最快。
師:你是怎樣看出來的?
生12:在這個階段折線最“陡”,說明這個階段的數據變化幅度最大。
師:小李身高在全市男生中所占的位置有變化嗎?
生13:有變化。從統計圖上看,小李身高在一、二年級時低于全市男生平均身高,在三年級時與全市男生平均身高相同,在四年級至六年級時高于全市男生平均身高。
師:據統計,全市九年級男生的平均身高是164厘米,請你預測一下三年后小李在九年級時的身高是多少。
生14:在三年內,全市男生平均身高可能增長164-153=11(厘米),所以按照這樣估算,小李在三年后九年級時的身高可能也會增長11厘米,為154+11=165(厘米)。
師:復式折線統計圖不但能夠表示兩組數據的多少和增減變化,還能夠預測數據的發展趨勢。
讀懂統計圖,從統計圖中提取有效信息,是培養學生數據分析能力的重要舉措。教學中,教師引導學生對復式折線統計圖展開多層次的數據分析和描述,不但凸顯了復式折線統計圖的獨特優勢,還培養了學生通過解讀統計圖分析數據信息的能力;此外,教師引導學生以動態的觀點觀察、分析數據的變化規律,預測三年后小李的身高,提升了學生數據分析的深度,使學生的統計思維變得更加深刻而靈活。
統計知識的教學不能把主要精力聚焦于某個知識點,而應該致力于培養學生的數據統計意識和數據分析能力,使學生切身體會到數據統計在認識外部世界中起到的重要作用。因此,教師在教學中應該以培養學生數據分析能力為核心,通過畫圖、讀圖等環節,使學生意識到利用統計的方式解決問題的獨特優勢,并引導學生通過對數據的對比和分析,預測數據的未來發展趨勢,把學生的數據分析能力提升到一個新的層次。

