核心素養(yǎng)理念下高效課堂的構(gòu)建策略

摘 要：以培養(yǎng)核心素養(yǎng)為目標(biāo)的課堂，需要具體的數(shù)學(xué)方法與思維來提供支撐，而通過有效問題來設(shè)計和驅(qū)動課堂教學(xué)，則是構(gòu)建高效課堂的有效途徑，引領(lǐng)學(xué)生開啟思維，解決學(xué)生對知識的需求，讓知識自主生成，讓數(shù)學(xué)活動和數(shù)學(xué)素養(yǎng)進行相互轉(zhuǎn)化，

從而真正地發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng).

關(guān)鍵詞：核心素養(yǎng);高效課堂;有效問題

中圖分類號：G632?? 文獻(xiàn)標(biāo)識碼：A?? 文章編號：1008-0333（2022）23-0023-03

收稿日期：2022-05-15

作者簡介：李華（1979.2-），女，本科，中學(xué)高級教師，從事初中數(shù)學(xué)教學(xué)研究.

核心素養(yǎng)是人適應(yīng)信息時代和知識社會的需要.數(shù)學(xué)核心素養(yǎng)包含數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運算、直觀想象、數(shù)據(jù)分析等六個方面.那么聚焦學(xué)科核心素養(yǎng)的深度學(xué)習(xí)，培育數(shù)學(xué)核心素養(yǎng)需要什么樣的課堂呢？筆者認(rèn)為，教師在組織教學(xué)的過程中，抓住學(xué)習(xí)內(nèi)容或教學(xué)內(nèi)容的關(guān)鍵特征，通過有效問題來設(shè)計和驅(qū)動課堂教學(xué)，是培養(yǎng)學(xué)生核心素養(yǎng)，構(gòu)建高效課堂的有效途徑.

下面筆者結(jié)合課例《相似三角形中的面積問題》談一談如何讓有效問題引領(lǐng)課堂，從而構(gòu)建核心素養(yǎng)下的高效課堂教學(xué)的嘗試.

問題是學(xué)習(xí)數(shù)學(xué)的直接驅(qū)動力，是數(shù)學(xué)教學(xué)活動的主心骨，那如何巧妙設(shè)問才能讓學(xué)生質(zhì)疑，進而有探究的意愿，又如何讓學(xué)生在探究問題中激發(fā)興趣，獲得數(shù)學(xué)知識和基本活動經(jīng)驗，從而鍛煉能力，提升素養(yǎng)，這是我們在課程設(shè)計時需重點思考的問題.

1 通過合理創(chuàng)設(shè)問題情境引入課題

師：看到課題中的“相似三角形的面積”，你們想到了什么？

生：相似三角形的面積比等于相似比的平方.

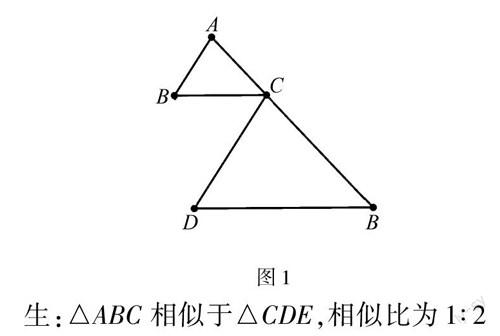
師：請看例1：如圖1，AB∥CD，BC∥DE，△ABC的面積為1，△CDE的面積為4.你能得到什么結(jié)論嗎？ 圖1

生：△ABC相似于△CDE，相似比為1∶2

師：下面請大家在圖1上添1條或者2條線段，在新圖形的基礎(chǔ)上，設(shè)置一個你能求的關(guān)于面積的問題.

教師先拋出一個非常基本的相似問題，提出添一條或兩條線段，設(shè)置一個關(guān)于面積的問題.這個問題是建立在學(xué)生原有的認(rèn)知基礎(chǔ)上，考慮了學(xué)生的最近發(fā)展區(qū).問題的開放型設(shè)計，促使學(xué)生發(fā)散思維，積極思考，尋找解決問題的方法和途徑.因為是開放性問題易放難收，容易偏離主題，所以教師在設(shè)置問題時明確了條件“添一條或兩條輔助線”并且是“關(guān)于面積的問題”，保證問題的有效性.

這個問題從不同層面激發(fā)了學(xué)生的學(xué)習(xí)興趣，活躍了學(xué)生的思維，帶動學(xué)生快速融入課堂，為后續(xù)的思維活動做好準(zhǔn)備.

2 設(shè)置變式探究型問題激發(fā)深度學(xué)習(xí)

師：若上題中△ABC的面積仍為1，將△CDE的面積改為2，你還能求上面提出的問題嗎？

師：若將上題中△ABC的面積記為S1，△CDE的面積記為S2，你還能求上面提出的問題嗎？

生：（獨立思考，小組合作，以小組為單位進行匯報）

學(xué)生匯報結(jié)果：SAEF=（S1+S2）2，S平行四邊形BCDF=2S1S2

（SΔBCD=S1S2）

例2 如圖2，AB∥CD，BC∥DE，△ABC的面積為2，△CDE的面積為3，你能直接給出△AEF的面積，平行四邊形BCDF和△BCD的面積嗎？

例3 如圖3，AB∥CD，BC∥DF，△ABC的面積為4，△CDE的面積為16，你能直接給出△AEF的面積，平行四邊形BCDF和△BCD的面積嗎？

師：請大家思考，滿足這兩個結(jié)論的圖形，有怎樣的特征呢？我們是如何解決的呢？

生：滿足三角形的兩邊分別平行.找準(zhǔn)基本圖形，直接應(yīng)用結(jié)果.

在學(xué)生編題的基礎(chǔ)上改變?nèi)切蚊娣e，由特殊到一般得出面積公式，并初步解決類似問題，在學(xué)生有了充足的活動感悟后提出：有這兩個結(jié)論的圖形，有怎樣的共同特征呢？我們是如何解決的呢？促使學(xué)生思考自己的學(xué)習(xí)過程和學(xué)習(xí)策略，這樣的反思與總結(jié)，常常是指向數(shù)學(xué)方法與數(shù)學(xué)思維的，幫學(xué)生形成關(guān)鍵能力.

例4 如圖4，正方形DEFG為△ABC的內(nèi)接正方形，△ADE的面積為1，△EFC的面積為1 ，△BDG的面積為3，則這個正方形的邊長為.

問：這個圖形與基本圖形有什么異同點，可以怎么轉(zhuǎn)化呢？

例5 如圖5，在△BCF中，CF∥DE∥AG，EF∥AD∥GH，△DEF的面積為4，△ADG的面積為1，則圖中三個陰影三角形的面積和為.

問：這個圖形中能找出所有的基本圖形嗎？

例6 如圖6，過△ABC內(nèi)部一點P分別作△ABC的三邊的平行線得三個△PDF、△PGH、△PIE三角形的面積分別為1，4，9，則△ABC的面積是.

師：請同學(xué)們獨立思考，并嘗試?yán)枚喾N解法解決.

通過例4引導(dǎo)學(xué)生利用轉(zhuǎn)化思想變正方形為平行四邊形，例5由多個基本圖形依次組成，例6則由基本圖形疊加而成，思考空間呈螺旋上升，教師的引導(dǎo)也逐步放手.例6學(xué)生給出了三種解法，分別是直接提煉基本圖形，例用相似比轉(zhuǎn)化，例用平移轉(zhuǎn)化為基本圖形.

此時教師調(diào)整了原有的設(shè)計，在學(xué)生給出的解法上繼續(xù)提出了問題，進而激發(fā)學(xué)生繼續(xù)思考.

追問：例6同學(xué)們給出的如圖平移的方法，

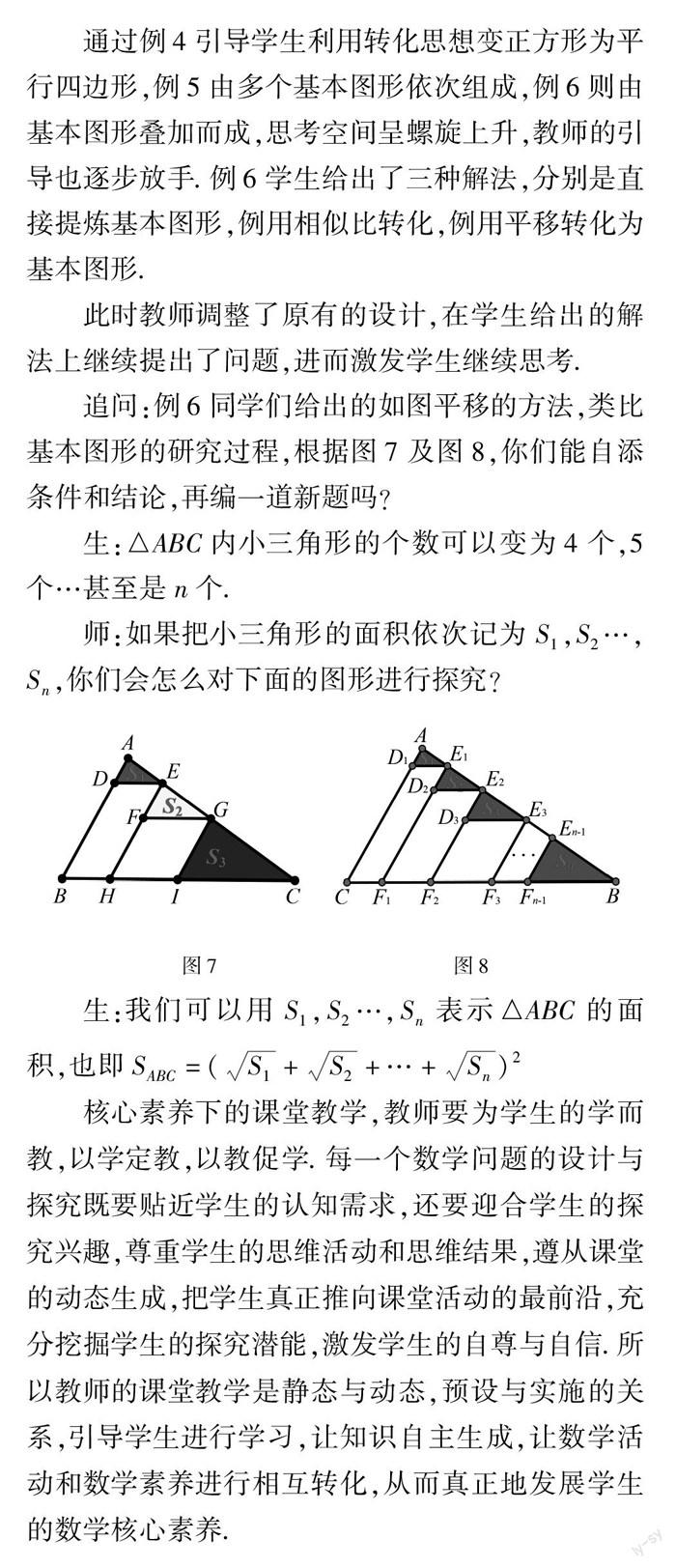
類比基本圖形的研究過程，根據(jù)圖7及圖8，你們能自添條件和結(jié)論，再編一道新題嗎？

生：△ABC內(nèi)小三角形的個數(shù)可以變?yōu)?個，5個…甚至是n個.

師：如果把小三角形的面積依次記為S1，S2…，Sn，你們會怎么對下面的圖形進行探究？

生：我們可以用S1，S2…，Sn表示△ABC的面積，也即SABC=（S1+S2+…+Sn）2

核心素養(yǎng)下的課堂教學(xué)，教師要為學(xué)生的學(xué)而教，以學(xué)定教，以教促學(xué).每一個數(shù)學(xué)問題的設(shè)計與探究既要貼近學(xué)生的認(rèn)知需求，還要迎合學(xué)生的探究興趣，尊重學(xué)生的思維活動和思維結(jié)果，遵從課堂的動態(tài)生成，把學(xué)生真正推向課堂活動的最前沿，充分挖掘?qū)W生的探究潛能，激發(fā)學(xué)生的自尊與自信.所以教師的課堂教學(xué)是靜態(tài)與動態(tài)，預(yù)設(shè)與實施的關(guān)系，引導(dǎo)學(xué)生進行學(xué)習(xí)，讓知識自主生成，讓數(shù)學(xué)活動和數(shù)學(xué)素養(yǎng)進行相互轉(zhuǎn)化，從而真正地發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng).

3 引導(dǎo)學(xué)生發(fā)現(xiàn)問題提出問題

在數(shù)學(xué)的核心素養(yǎng)中，學(xué)會發(fā)現(xiàn)問題是一項非常重要的能力，我們的課堂不僅是教師在提出問題，更應(yīng)是學(xué)生因解決問題繼而能提出問題，因為只有學(xué)生能夠發(fā)現(xiàn)問題，才會促進學(xué)生更加深入地挖掘和學(xué)習(xí)，在解決問題的同時提高自己的數(shù)學(xué)學(xué)習(xí)能力.在此過程中，教師要注意為學(xué)生創(chuàng)造出一種輕松活躍的氛圍，讓學(xué)生能夠真實地表達(dá)出自己的想法.

在能力提升2的解決過程中，學(xué)生不僅給出了不同的解決方案，還提出了新的問題，如求5個三角形的面積和，求第n個三角形面積等問題，同樣在創(chuàng)設(shè)問題情境的添線編題中直接連接BD的學(xué)生，提出沒有平行四邊形的面積那該如何直接求出△BCD的面積，引發(fā)同學(xué)們的共同思考;深度探究的環(huán)節(jié)也都是嘗試著讓學(xué)生不斷的提出問題，解決問題，學(xué)生的思維顯得非常活躍.

在核心素養(yǎng)的背景下，數(shù)學(xué)方法和思維能力是支撐以必備品格與關(guān)鍵能力為基點的核心素養(yǎng)培育的基礎(chǔ)，其涉及的數(shù)學(xué)抽象，邏輯推理，數(shù)學(xué)建模，數(shù)學(xué)運算，直觀想象，數(shù)據(jù)分析等方面，都需要具體的數(shù)學(xué)方法與思維來提供支撐.因此本，節(jié)課在經(jīng)歷問題的提出-分析-解決-升華-運用-創(chuàng)新的教學(xué)環(huán)節(jié)中，教師有意識地引導(dǎo)學(xué)生理解運用數(shù)學(xué)思想方法， 經(jīng)歷了從特殊到一般的過程，蘊含了類比轉(zhuǎn)化的思想方法和利用基本圖形化繁為簡，化難為易的轉(zhuǎn)化思想，開啟了學(xué)生思維，打造i靈動課堂.

裴光亞先生指出：如何判斷一節(jié)課是否成功？就看它有沒有以核心素養(yǎng)為目標(biāo)的導(dǎo)向，有沒有問題驅(qū)動，有沒有抽象，推理和建模的架構(gòu)，有沒有激發(fā)學(xué)生想象，砥礪品質(zhì)的生態(tài)環(huán)境，所以本節(jié)課備課時就是圍繞培養(yǎng)學(xué)生的核心素養(yǎng)，通過創(chuàng)新問題情境，引發(fā)學(xué)生深度思考，讓學(xué)生去發(fā)現(xiàn)問題，提出問題，分析問題，解決問題，應(yīng)用問題，創(chuàng)新問題，使其思，能力得到提升.以培養(yǎng)核心素養(yǎng)為目標(biāo)的課堂，需要教學(xué)智慧，需要教師砥礪前行.

參考文獻(xiàn)：

[1] 呂井春.核心素養(yǎng)背景下初中數(shù)學(xué)教學(xué)設(shè)計需要關(guān)注的基本問題[J].數(shù)學(xué)教學(xué)通訊（中旬），2018（9）：54-56.

[2] 張宜興.創(chuàng)新問題情境引發(fā)深度思考[J].中學(xué)數(shù)學(xué)教學(xué)參考（中旬），2018（5）：9-11.

[責(zé)任編輯：李 璟]